Методы оптимизации топологии имеют эвристический характер. Топология связана с выбором пропускных способностей, поскольку отсутствие прямой связи между некоторой парой узлов можно интерпретировать как линию с нулевой пропускной способностью в каждом из направлений. Именно так работает метод исключения ветвей.
Топология, созданная каким-то случайным образом, едва ли будет приемлемой и связной. Если же сеть связна, то может потребоваться внести в топологию сети некоторые изменения, улучшающие ее свойства и сохраняющие связность. В методе перестановки ветвей вносимые в топологию изменения должны по возможности не менять степеней узлов.
На рис. 2.2 показан способ, с помощью которого можно исследовать различные топологии сети и накапливать локально-оптимальные варианты. На первом шаге этого алгоритма для построения топологий используются случайные числа, причем линии связи вводятся таким образом, чтобы они соединяли узлы с наименьшими степенями. При таком способе построения линий узел со степенью два появится только после того, как степенью каждого из узлов сети будет единица. В ходе дальнейшей оптимизации происходит введение локальных изменений топологии, например, методом перестановки ветвей. После каждой перестановки вновь проверяется связность сети, и, если она окажется ниже заданной, эта перестановка отвергается. В основной части этой процедуры для сети исследуемой топологии решается задача о распределении потока и выборе пропускной способности, после чего трафик в сети увеличивается до тех пор, пока не будет достигнута верхняя граница средней задержки. Величина пропускной способности регистрируется, определяется стоимость сети, и теперь можно решить, удовлетворяет ли данная сеть необходимым критериям.
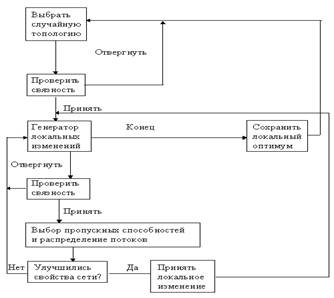
Рис. 2.2. Эвристический метод оптимизации топологии
Топологии, выдержавшие проверку на связность и удовлетворяющие критериям на производительность, подвергаются дальнейшим улучшениям. Когда возможность локальных изменений исчерпывается, полученный вариант запоминается вместе со своими характеристиками как локальный оптимум и программа снова обращается к генератору за новой топологией. После того как будет оптимизировано достаточное число начальных вариантов топологий сети, строится зависимость, определяющая стоимость и уровень трафика для всех полученных локальных решений и являющаяся результатом процесса оптимизации.
 2015-02-04
2015-02-04 419
419








