Сначала кратко напомним некоторые математические понятия и факты.
Теорема 1. Если функция непрерывна на замкнутом ограниченном множестве конечномерного евклидова пространства, то она ограничена на нем и достигает наименьшего и наибольшего значений.
Определение 1. Любые m переменных системы m линейных уравнений с n переменными (m < n) называются основными, если определитель из коэффициентов при них отличен от нуля. Тогда остальные n - m переменных называются неосновными (свободными).
Определение 2. Базисным решением системы m линейных уравнений с n переменными (m < n) называется всякое её решение, в котором неосновные переменные имеют нулевое значение.
Определение 3. Решение системы m линейных уравнений с n переменными (m < n) называется допустимым, если в нём все основные переменные неотрицательны.
Теорема. Существует взаимнооднозначное соответствие между угловыми точками множества допустимых решений системы m линейных уравнений с n переменными (m < n) и её допустимыми базисными решениями.
Сначала необходимо ЗЛП привести к каноническому виду (КЗЛП).
Доказано, что оптимальное решение ЗЛП (если оно существует и притом единственное) совпадает с одним из допустимых базисных решений системы ограничений, следовательно, с угловой точкой многогранника решений.
Однако для реальных задач число допустимых базисных решений может быть очень велико и провести перебор всех угловых точек многогранника затруднительно. Этот перебор можно сократить, используя идею симплексного метода (метод предложен в 1949 г. американским ученым Дж. Данцигом).
Для реализации симплекс-метода – метода последовательного улучшения плана – необходимо знать три основные операции:
1) способ определения какого-либо первоначального допустимого базисного решения;
2) алгоритм перехода от одного допустимого базисного решения к другому;
3) критерий проверки оптимальности решения.
Замечание. Если первоначальное базисное решение недопустимо, то удобно использовать симплекс-метод с искусственным базисом.
9. Двойственность в линейном программировании, свойства двойственных оценок и их использование в анализе оптимального плана
Рассмотрим основные понятия и выводы специального раздела линейного программирования — теории двойственности.
С каждой задачей линейного программирования определенным образом тесно связана другая линейная задача, называемая двойственной. Первоначальная задача называется исходной или прямой.
Связь исходной и двойственной задач заключается, в частности, в том, что решение одной из них может быть получено непосредственно из решения другой.
Хорошо разработанный математический аппарат линейного программирования позволяет не только получать с помощью эффективных вычислительных процедур оптимальный план, но и делать ряд экономически содержательных выводов, основанных на свойствах задачи, двойственной к исходной ЗЛП.
Каждая из задач двойственной пары фактически является самостоятельной задачей линейного программирования и может быть решена независимо от другой задачи. Однако при определении симплексным методом оптимального плана одной из задач находится решение и другой задачи.
Правило построения двойственной задачи по отношению к исходной задаче определяется системой соотношений:
| Исходная задача | Двойственная задача |
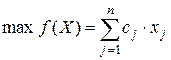 | 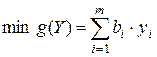 |
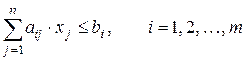 | 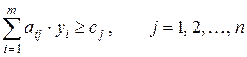 |
 |  |
Двойственная задача составляется согласно следующим правилам:
1) целевая функция исходной задачи формулируется на максимум, а целевая функция двойственной задачи — на минимум, при этом в задаче на максимум все неравенства в функциональных ограничениях имеют вид «£», а в задаче на минимум — «³».
2) матрица, составленная из коэффициентов при неизвестных в системе ограничений исходной задачи, и аналогичная матрица в двойственной задаче получаются друг из друга транспонированием;
3) число переменных в двойственной задаче равно числу функциональных ограничений исходной задачи; число ограничений двойственной задачи равно числу переменных в исходной задаче;
4) коэффициентами при неизвестных в целевой функции двойственной задачи являются свободные члены в системе ограничений исходной задачи, а правыми частями в ограничениях двойственной задачи — коэффициенты при неизвестных в целевой функции исходной задачи;
5) каждому ограничению одной задачи соответствует переменная другой задачи: номер переменной совпадает с номером ограничения; при этом ограничению, записанному в виде неравенства «£», соответствует переменная, связанная условием неотрицательности.
Основные утверждения о двойственных задачах содержатся в двух следующих теоремах
Теорема 1 (основная теорема двойственности). Если одна из двойственных задач разрешима, то разрешима и другая, причем экстремальные значения целевых функций задач равны: 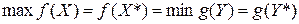 . Если одна из двойственных задач неразрешима, то неразрешима и другая.
. Если одна из двойственных задач неразрешима, то неразрешима и другая.
Теорема 2 (о дополняющей нежесткости). Если при подстановке компонент оптимального плана в систему ограничений исходной задачи i -е ограничение обращается в неравенство, то i -я компонента оптимального плана двойственной задачи равна нулю. Если i -я компонента оптимального плана двойственной задачи положительна, то i -е ограничение исходной задачи удовлетворяется ее оптимальным решением как строгое равенство.
То есть для оптимальных планов двойственных задач имеют место соотношения:
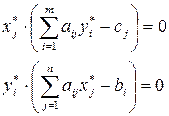 ,
,
которые позволяют, зная оптимальное решение одной из двойственных задач, найти оптимальное решение другой задачи.
 2015-02-27
2015-02-27 1148
1148
