Продольные колебания консольного стержня постоянного сечения

Найдем матрицы инерции и жесткости для элемента первого порядка длиной Имеем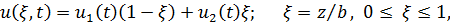

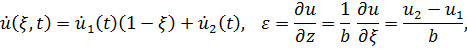
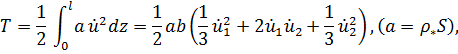
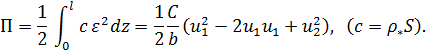
Разобьем стержень длиной 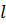на два элемента длиной (рис. 7.13,в) и, складывая кинетические и потенциальные энергии элементов, с учетом выполнения получим:

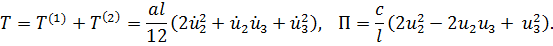
Уравнения Лагранжа имеют вид:

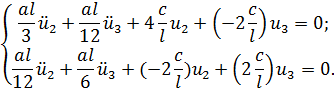
Отыскивая решение в виде получим:

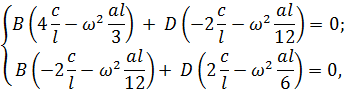
и, приравнивая нулю определитель, получим частотное уравнение:

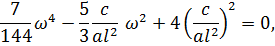
откуда ,

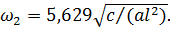
Точные значения собственных частот равны:

.

Первая собственная частота превышает точную на вторая .

Заметим, что превышение приближенных значений собственных частот над точными значениями неслучайно – при использовании в приближенном решении аппроксимации перемещений система с бесконечным числом степеней свободы всегда «мягче» построенных дискретизацией расчетных моделей.