Вариацией значений какого-либо признака в совокупности называется различие его значений у разных единиц данной совокупности в один и тот же момент либо за один и тот же период времени.
Причиной вариации являются разные условия существования разных единиц совокупности. Например, огромное число причин влияет на рост человека, его заработной платы и т.д.
Первым этапом статистического изучения вариации является построение вариационного ряда (ряда распределения) – упорядоченного распределения единиц совокупности по возрастающим либо по убывающим значениям признака и подсчет числа единиц с тем или иным значением признака.
Формы вариационных рядов:
1. Ранжированный ряд – перечень отдельных единиц совокупности в порядке возрастания (убывания) изучаемого признака.
2. Дискретный ряд – таблица, состоящая из двух строк (столбцов): конкретных значений варьирующего признака Xi и числа единиц совокупности с данным значением признака fi – частот (frequency).
Строится в том случае, когда признак принимает дискретные значения и число этих значений невелико. Число групп в дискретном вариационном ряду определяется числом реально существующих значений варьирующего признака.
3. Интервальный вариационный ряд – это таблица, состоящая из двух столбцов (строк) – интервалов варьирующего признака Xi и числа единиц совокупности, попадающих в данный интервал (частот – fi), или долей этого числа в общей численности совокупностей (частостей – di).. Строится в случаях, когда:
• признак принимает дискретные значения, но число их велико;
• признак принимает любые значения (и дискретные, и дробные).
Количество интервалов можно определять двумя способами:
1) по формуле Стерджесса: 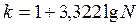 ,
,
где k – число групп (округляемое до ближайшего целого числа) – это функция объема данных (N);
N – численность совокупности.
2) по смыслу в зависимости от целей исследования.
Зная число групп, рассчитывают длину (размах) интервала по формуле:
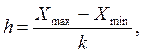
где X max и X min– максимальное и минимальное значения в совокупности.
Интервалы могут быть равные и неравные по длине. Если приходится иметь дело с неравными интервалами, то для сопоставимости нужно частоты привести к единице интервала. Полученное соотношение называют плотностью распределения (σ):
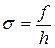 .
.
В анализе вариационного ряда значительную помощь оказывает его графическое изображение.
Дискретный вариационный ряд изображается с помощью полигона (от греческого «полигон» – многоугольник).
Интервальный вариационный ряд - изображается с помощью гистограммы (от греческого «гистос» – ткань, строение).
Преобразованной формой вариационного ряда является ряд накопленных частот.
По накопленным частотам строят кумуляту (распределение «меньше, чем...») и огиву (распределение «больше, чем...»).
М едиана – величина варьирующего признака, делящая совокупность на две равные по численности части (со значением признака меньше медианы и со значением признака больше медианы).
В интервальном ряду распределения для нахождения медианы применяется формула:
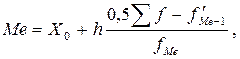
где X 0 – нижняя граница интервала, в котором находится медиана;
h – размах медианного интервала (разность между его верхней и нижней границей);
f – накопленная частота в интервале, предшествующем медианному;
f Me – частота в медианном интервале.
Мода – наиболее часто встречающееся значение признака (т.е. значение признака с наибольшей частотой).
Для интервального ВР мода, например доходов населения, определяется по формуле:
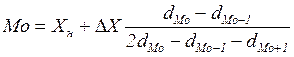
где ХН – нижняя граница интервала с наиболее распространенным доходом, руб.;
∆Х – размах этого интервала, руб.;
dМо – доля населения с наиболее распространенным доходом;
dМо-1 – доля населения с предыдущим интервалом дохода;
dМо+1 – доля населения с последующим интервалом дохода;
Модальный интервал – интервал с наибольшей частотой.
Размах вариации – разность максимального и минимального значений признака в совокупности.
Дисперсия – средняя величина квадратов отклонений.
Следовательно, дисперсия от средней всегда меньше дисперсий, исчисленных от любых других величин, т.е. она имеет свойство минимальности.
Общая дисперсия измеряет вариацию признака во всей совокупности под влиянием всех факторов, обусловивших эту вариацию.
Межгрупповая дисперсия характеризует вариацию признака под влиянием признака-фактора, положенного в основу группировки.
Внутригрупповая (остаточная) дисперсия характеризует вариацию признака под влиянием всех остальных факторов, исключая признак-фактор, положенный в основу группировки.
Остаточные дисперсии рассчитываются по каждой группе, т.е. их количество равно количеству групп. Затем рассчитывается средняя из остаточных дисперсий:
Правило сложения дисперсий – закон, связывающий три вида дисперсий: общая дисперсия равна сумме межгрупповой и средней из остаточных дисперсий.
Среднее квадратическое отклонение (СКО) – обобщающая характеристика размеров вариации признака в совокупности. Оно выражается в тех же единицах измерения, что и признак.
Между 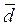 и
и 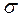 существует следующее примерное соотношение в случае, если фактическое распределение близко к нормальному:
существует следующее примерное соотношение в случае, если фактическое распределение близко к нормальному: 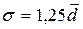
«Правило трех СИГМ».
В условиях нормального распределения существует следующая зависимость между величиной СКО и количеством наблюдений:
1) в пределах 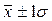 располагается 68,3% от общего количества наблюдений;
располагается 68,3% от общего количества наблюдений;
2) в пределах 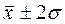 располагается 95,4% от общего количества наблюдений;
располагается 95,4% от общего количества наблюдений;
3) в пределах 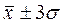 располагается 99,7% от общего количества наблюдений;
располагается 99,7% от общего количества наблюдений;
На практике почти не встречается отклонений, которые превышают 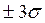 .
.
Контрольные вопросы
При подготовке к контрольным вопросам и выполнении контрольных заданий руководствоваться библиографическими источниками [1–3].
1. Вариация - это...?
______________________________________________________________________
______________________________________________________________________
______________________________________________________________________
______________________________________________________________________
______________________________________________________________________
______________________________________________________________________
2. Если все значения признака увеличить в 16 раз, то дисперсия:
• не изменится;
• увеличится в 16 раз;
• увеличится в 256 раз;
• увеличится в 4 раза;
• предсказать изменение дисперсии нельзя.
3. Чему равна межгрупповая дисперсия, если отсутствуют различия между вариантами внутри групп?
• единице;
• нулю;
• колеблется от нуля до единицы;
• общей дисперсии;
• средней из остаточных дисперсий.
4. Какой показатель вариации рассчитывается на основе центрального момента четвертого порядка?
______________________________________________________________________
______________________________________________________________________
______________________________________________________________________
______________________________________________________________________
______________________________________________________________________
______________________________________________________________________
5. В каком случае целесообразно построение интервального ВР?
______________________________________________________________________
______________________________________________________________________
______________________________________________________________________
______________________________________________________________________
______________________________________________________________________
______________________________________________________________________
 2015-02-27
2015-02-27 671
671








