Занятие 2. Методы интегрироваНИЯ

1. Непосредственное интегрирование

Простейшим из методов интегрирования является так называемое непосредственное интегрирование, суть которого состоит в том, что путем алгебраических, тригонометрических или других преобразований подынтегральное выражение приводят к такому виду, что искомый интеграл становится табличным или выражается через алгебраическую сумму табличных интегралов.

Примеры.

1.

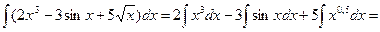
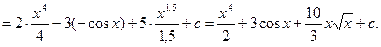
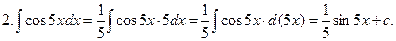
3.

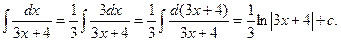
Замечание 1. (Об интегрировании в конечном виде)

Непрерывная на некотором промежутке функция всегда имеет на этом промежутке первообразную, но ее не всегда удается выразить конечным числом операций через элементарные функции. В этом случае говорят, что интеграл не берется в конечном виде.

Среди интегралов, не берущихся в конечном виде, большое прикладное значение имеет интеграл Пуассона 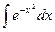, интегралы Френеля 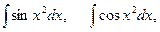интегральный логарифм и сводящийся к нему интеграл 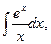интегральные синус и косинус: .

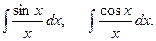В теории вероятностей большое значение имеет первообразная функции f(x) = 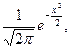называемая интегралом вероятностей.

Замечание 2. Иногда первообразные к одной той же функции имеют различный вид. Однако все сводится к различию в том, что понимается под С.

Примеры.

1).

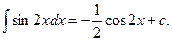
2).

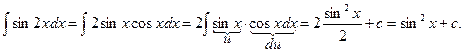
3) .

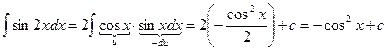Преобразуем:

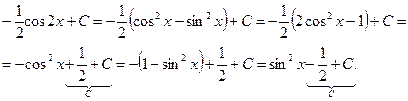
Итак, простейшим методом интегрирования является метод непосредственного интегрирования.