Неопределенный интеграл обладает следующими свойствами:
1) Неопределенный интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме интегралов от каждого слагаемого в отдельности:
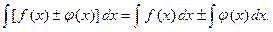 (1)
(1)
2) Постоянный множитель можно выносить за знак неопределенного интеграла:
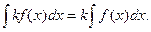 (2)
(2)
Оба свойства доказываются аналогично. Равенства (1) и (2) следует понимать в том смысле, что левая и правая их части отличаются на постоянные слагаемые.
Докажем, например, (2). Продифференцируем его:
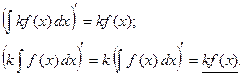
Т.е. левая и правая части равенства (2) являются первообразными для одной и той же функции.
Свойство доказано.
3) Производная от неопределенного интеграла равна подынтегральной функции, а дифференциал от неопределенного интеграла - подынтегральному выражению:
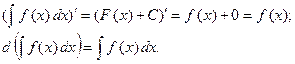
4) Неопределенный интеграл инвариантен относительно замены переменной х любой дифференцируемой функцией, т.е. если 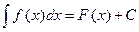 , то
, то
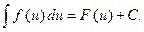 Если записать последнюю формулу подробнее, то получим:
Если записать последнюю формулу подробнее, то получим:
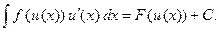
Докажем справедливость этого равенства дифференцированием левой и правой частей:
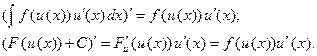
При вычислении неопределенных интегралов бывает полезно иметь в виду следующие правила.
I. Если 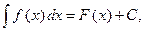 то
то 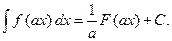
Действительно, дифференцируя левую и правую части этого равенства, получим:
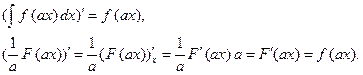
Производные от правой и левой частей равны.
II. Если 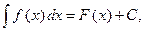 то
то 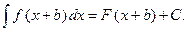
III. Если 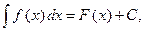 то
то 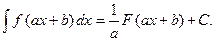
Эти равенства доказываются дифференцированием правой и левой частей равенств.
Итак, свойства неопределенного интеграла будут использованы в различных методах его вычисления.
Таблица основных формул интегрирования
Из определений первообразной и неопределенного интеграла, а также таблицы производных вытекает таблица основных интегралов, которую целесообразно записывать, используя свойства инвариантности неопределенного интеграла, для переменной интегрирования u, которая является некоторой дифференцируемой функцией от х.
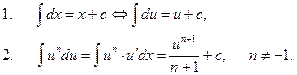
Проверим справедливость этой формулы: 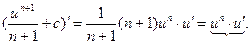
Получили подынтегральную функцию.
Аналогично проверяются следующие формулы: 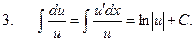
а) Если u > 0, то первообразной будет функция F(u) = lnu.
Проверяем: 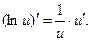
б) Если u < 0, то 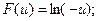
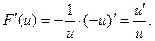
Следовательно, 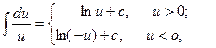 или:
или: 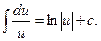
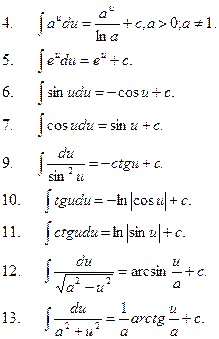 |
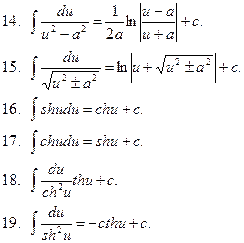
 2015-02-27
2015-02-27 3310
3310
