Контрольный расчет

1. Вычисляем групповые и общее средние значения:

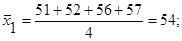
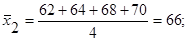
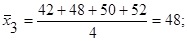
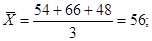
2. Составляем сумму квадратов отклонений групповых средних значений от общего среднего значения

=4((54-56)²+(66-56)²+(48-56)²)=672.

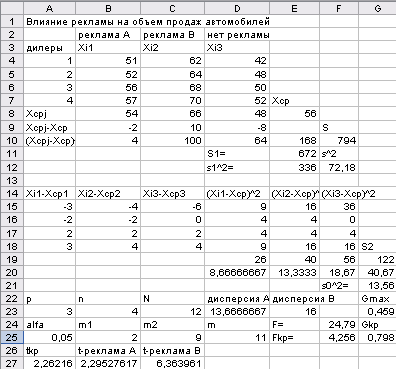
Т а б л и ц а 2.3

Результаты расчета в среде ЭТ

3. Составляем сумму квадратов отклонений наблюдавшихся значений каждой группы от среднего значения своей группы

=((51-54)²+(52-54)²+(56-54)²+(57-54)²)+…+

+((42-48)²+(48-48)²+(50-48)²+(52-48)²)=122.

4. Находим факторную и остаточную дисперсии

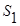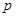= /( -1)=672/2=336; 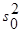= 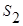/( (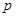 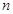-1))=122/9=13,55, .

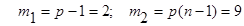5. Сумма квадратов общей изменчивости объема продаж равна 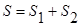=794, число степеней свободы 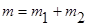=11, оценка общей или выборочной дисперсии =72,18.

6. Определяем расчетное значение 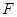- критерия

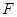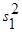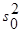= / =336/13,55=24,786.

7. C помощью статистической функции 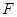РАСПОБР находим критическое значение 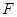- критерия при . .

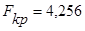Так как 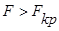, то влияние рекламы на объем продаж статистически значимо (существенно).

Сравнивая результаты расчета в среде ЭТ с контрольным расчетом, отмечаем их совпадение.

Т а б л и ц а 2.4

Расчетные формулы

Адрес	Формула	Адрес	Формула
B8	=СУММ(b4:b7)/$b$23	A15	=b4-b$8
E8	=СУММ(b8:d8)/a23	D15	=a15^2
B9	=b8-$e$8	D19	=СУММ(d15:d18)
B10	=b9^2	G19	=СУММ(d19:f19)
E10	=СУММ(b10:d10)	G21	=g19/c25
E11	=b23*e10	F24	=e12/g21
E12	=e11/b25	F25	=FРАСПОБР(a25;b25;c25)
D20	=d19/($b$23-1)	B25	=a23-1
D23	=(d20+$f$20)/2	C25	=a23*(b23-1)
D25	=b25+c25	G20	=СУММ(d20:f20)
A27	=CТЬЮДРАСПОБР(a25;c25)	B27	=(b8-$d$8)*КОРЕНЬ(2)/ КОРЕНЬ($g$21)
F10	=e11+g19	G23	=f20/g20
F12	=f10/d25	M9	=СУММ(m6:m8)
N7	=m8/m9

В таблице 2.5 приведена сводка дисперсионного анализа влияния рекламы на объем продаж автомобилей, полученная с помощью инструмента Однофакторный дисперсионный анализ пакета анализа. Диалоговое окно инструмента «Однофакторный дисперсионный анализ» приведено на рис. 2.1.

Т а б л и ц а 2.5

Дисперсионный анализ влияния рекламы на объем продаж

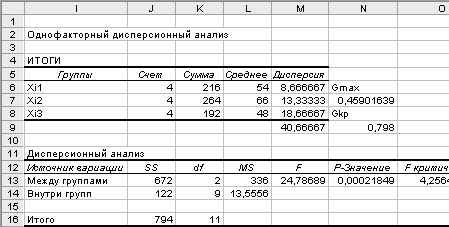
В таблице 5 обозначено: 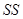- суммы квадратов; 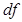- степени свободы; 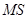- дисперсии; 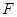- расчетное значение 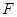- критерия Фишера; 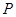- значение. Если 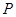< 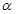=0,05, то исследуемый фактор статистически значим. Дополнительно выполнена проверка однородности дисперсий ошибок измерений.