Основные понятия. Определение. Производной функции у = f (x) в точке х называется предел , если он существует и конечен

Определение. Производной функции у = f (x) в точке х называется предел 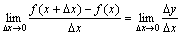, если он существует и конечен.
Функция у=f(x) называется дифференцируемой в точке х. Она всегда будет и непрерывной в этой точке.
Производная обозначается .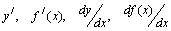
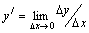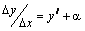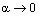Имеем . По определению предела функции , где при 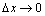. Отсюда ∆ y=y' ·∆ x+ α·∆ x.
При малых значениях ∆ x и при 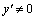имеем .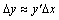
Определение. Главная часть y' ∆ x приращения ∆ y функции, линейная относительно ∆ x, называется дифференциалом функции и обозначается dy=y' ∆ x.
Положив у=х, получим dx=(x)' ∆ x= 1·∆ x= ∆ x и поэтому dy=y'dx.
Эта формула верна и в том случае, если х есть функция новой переменной t.