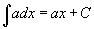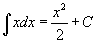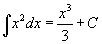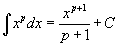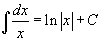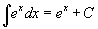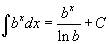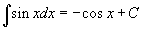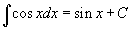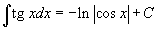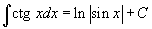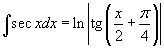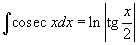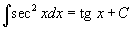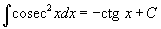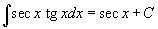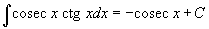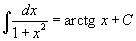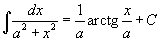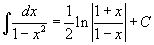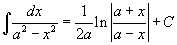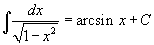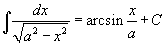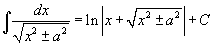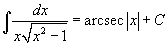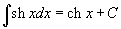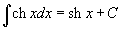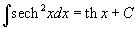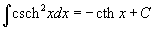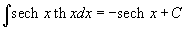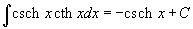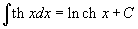Связь между непрерывностью и дифференцируемостью функции. Если функция f (x) дифференцируема в некоторой точке, то она непрерывна в этой точке. Обратное неверно: непрерывная функция может не иметь производной.
С л е д с т в и е. Если функция разрывна в некоторой точке, то она не имеет производной в этой точке.
| П р и м е р. | Функция y = | x | (рис.3) всюду непрерывна, но она не имеет производной при x = 0, так как в этой точке не существуеткасательной к графику этой функции. (Подумайте, почему?) |
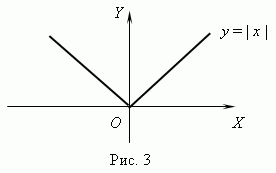
Достаточные признаки монотонности функции.
Если f ’(x) > 0 в каждой точке интервала (a, b), то функция f (x) возрастает на этом интервале.
Если f ’(x) < 0 в каждой точке интервала (a, b), то функция f (x) убывает на этом интервале.
Теорема Дарбу. Точки, в которых производная функции равна 0 или не существует, делят область определения функции на интервалы, внутри которых производная сохраняет знак.
Используя эти интервалы, можно найти интервалы монотонности функций, что очень важно при их исследовании.

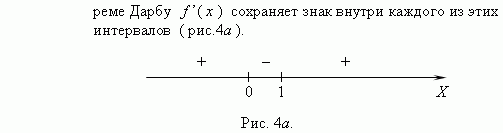
Следовательно, функция возрастает на интервалах (- 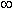 , 0) и (1, +
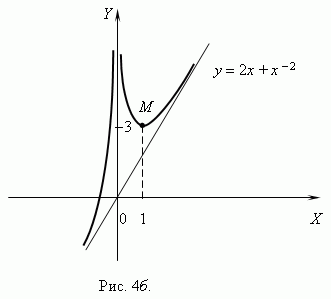
, 0) и (1, + 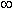 ) и убывает на интервале (0, 1). Точка x = 0 не входит в область определенияфункции, но по мере приближения x к 0 слагаемое x - 2 неограниченно возрастает, поэтому функция также неограниченно возрастает. В точке x = 1 значение функции равно 3. В соответствии с этим анализом мы можем построить график функции (рис.4 б).
) и убывает на интервале (0, 1). Точка x = 0 не входит в область определенияфункции, но по мере приближения x к 0 слагаемое x - 2 неограниченно возрастает, поэтому функция также неограниченно возрастает. В точке x = 1 значение функции равно 3. В соответствии с этим анализом мы можем построить график функции (рис.4 б).
Примеры: 1. Найти производные следующих функций:
а) 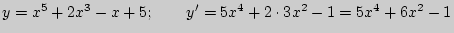 ;
;
б) 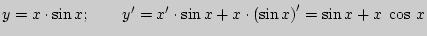 ;
;
в) 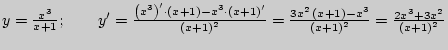 ;
;
г) 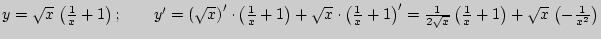 ;
;
д) 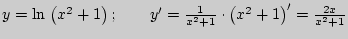 .
.
2. Составить уравнение касательной к графику функции 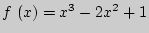 в точке с абсциссой 2.
в точке с абсциссой 2.
Решение: общий вид уравнения: 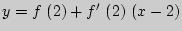 ;
;
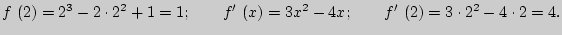
Тогда уравнение касательной примет вид:  .
.
3. Найти промежутки возрастания и убывания функции  .
.
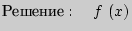 убывает, если
убывает, если 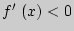 ;
; 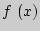 возрастает, если
возрастает, если 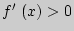 .
.
Для заданной функции 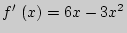 .
.
Найдем экстремумы заданной функции из уравнения 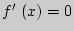 :
:
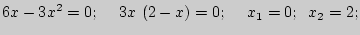
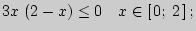
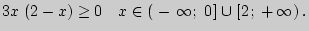
Итак, заданная функция возрастает на промежутках  и убывает на отрезке
и убывает на отрезке  .
.
4. Найти наибольшее и наименьшее значения функции 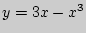 на отрезке
на отрезке 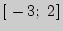 .
.
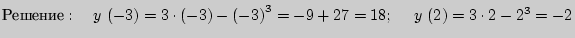 ;
;
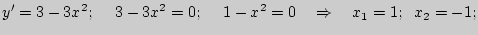
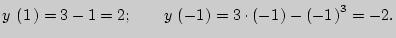
Наибольшее значение 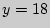 достигается при
достигается при 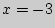 .
.
Наименьшее значение 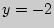 достигается при
достигается при 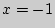 и
и  .
.
5. Точка движется по прямой, причем пройденный путь определяется формулой 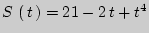 . Найти ее скорость в момент времени
. Найти ее скорость в момент времени  .
.
Решение: Воспользуемся определением мгновенной скорости 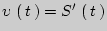 .
.
В нашем случае 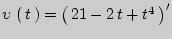 .
.
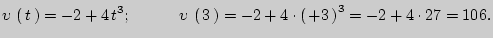
Ответ: 106.
6. Из квадратного листа жести со стороной 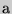 см изготавливают коробку. Для этого от его углов отрезают одинаковые квадраты и загибают края по пунктирным линиям. При каких размерах отрезаемых квадратов объем коробки будет наибольшим? Найти этот объем.
см изготавливают коробку. Для этого от его углов отрезают одинаковые квадраты и загибают края по пунктирным линиям. При каких размерах отрезаемых квадратов объем коробки будет наибольшим? Найти этот объем.
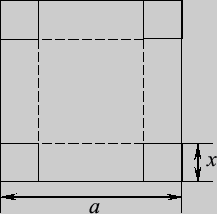
Решение: Обозначим сторону каждого из отрезаемых квадратов за 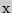 (см). Тогда дно коробки будет квадратом со стороной
(см). Тогда дно коробки будет квадратом со стороной 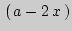 (см). Высота коробки составит
(см). Высота коробки составит 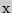 (см). Представим объем коробки формулой:
(см). Представим объем коробки формулой: 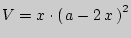 (см
(см 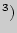 .
.
Теперь задача заключается в нахождении наибольшего значения функции 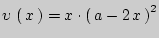 на интервале
на интервале 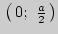 . Для нахождения точек экстремума составим уравнение
. Для нахождения точек экстремума составим уравнение 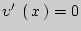 .
.
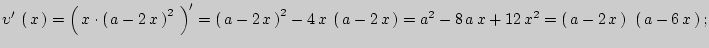
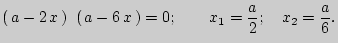
Но 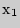 не принадлежит интервалу
не принадлежит интервалу 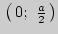 .
.
Рассмотрим точку 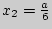 . При переходе через нее производная меняет свои значения с положительных на отрицательные. Следовательно, в точке
. При переходе через нее производная меняет свои значения с положительных на отрицательные. Следовательно, в точке 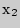 функция
функция 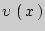 достигает локального максимума.
достигает локального максимума.
Критическая точка 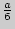 на интервале
на интервале 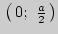 единственная, следовательно, она является точкой максимума исследуемой функции на интервале
единственная, следовательно, она является точкой максимума исследуемой функции на интервале 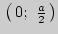 . Это значит, что наибольший объем изготавливаемой коробки будет достигаться, если от углов исходного листа жести отрезать квадраты со стороной
. Это значит, что наибольший объем изготавливаемой коробки будет достигаться, если от углов исходного листа жести отрезать квадраты со стороной 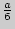 (см).
(см).
Вычислим наибольший объем коробки:
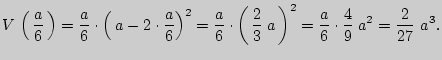
https://cito-web.yspu.org/link1/metod/met146/node15.html
| Неопределенный интеграл и его свойства. Таблица интегралов. | ||||||||||||||||||||||||||||||||
Определение первообразной и неопределенного интеграла Функция F (x) называется первообразной функции f (x), если 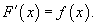 Множество всех первообразных некоторой функции f (x) называется неопределенным интегралом функции f (x) и обозначается как Множество всех первообразных некоторой функции f (x) называется неопределенным интегралом функции f (x) и обозначается как 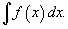 Таким образом, если F - некоторая частная первообразная, то справедливо выражение Таким образом, если F - некоторая частная первообразная, то справедливо выражение 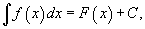 где С - произвольная постоянная. Свойства неопределенного интеграла В приведенных ниже формулах f и g - функции переменной x, F - первообразная функции f, а, k, C - постоянные величины. · где С - произвольная постоянная. Свойства неопределенного интеграла В приведенных ниже формулах f и g - функции переменной x, F - первообразная функции f, а, k, C - постоянные величины. · 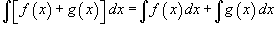 · · 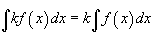 · · 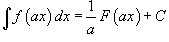 · · 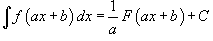 | ||||||||||||||||||||||||||||||||
Таблица интегралов В формулах ниже предполагается, что a, p (p ≠ 1), C - действительные постоянные, b - основание показательной функции (b ≠ 1, b > 0).
| ||||||||||||||||||||||||||||||||
| Пример 1 | ||||||||||||||||||||||||||||||||
Вычислить 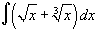 . Решение. . Решение. 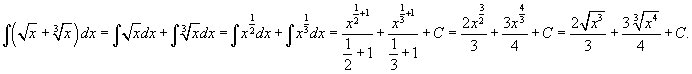 | ||||||||||||||||||||||||||||||||
| Пример 2 | ||||||||||||||||||||||||||||||||
Вычислить интеграл 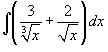 . Решение. Преобразуя выражение и применяя формулу для интеграла степенной функции, получаем . Решение. Преобразуя выражение и применяя формулу для интеграла степенной функции, получаем 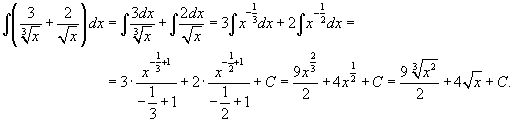 | ||||||||||||||||||||||||||||||||
| Пример 3 | ||||||||||||||||||||||||||||||||
Вычислить 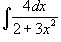 . Решение. Используем табличный интеграл . Решение. Используем табличный интеграл 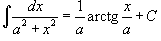 . Тогда . Тогда 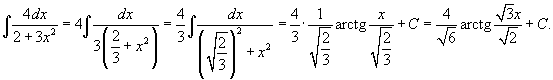 | ||||||||||||||||||||||||||||||||
| Пример 4 | ||||||||||||||||||||||||||||||||
Вычислить 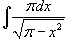 . Решение. Воспользовавшись табличным интегралом . Решение. Воспользовавшись табличным интегралом 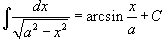 , находим , находим 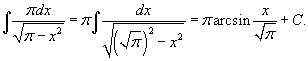 |
https://www.math24.ru/indefinite-integral.html
| Определенный интеграл. Формула Ньютона-Лейбница. | ||||||
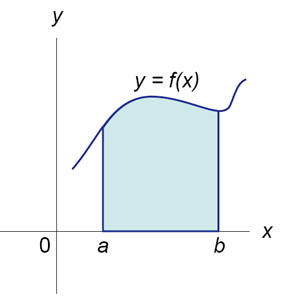
Пусть функция f (x) непрерывна на замкнутом интервале [ a, b ]. Определенный интеграл от функции f (x) в пределах от a до b вводится как предел суммы бесконечно большого числа слагаемых, каждое из которых стремится к нулю: 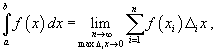 где где 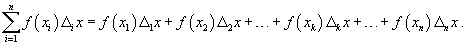 Свойства определенного интеграла Ниже предполагается, что f (x) и g (x) - непрерывные функции на замкнутом интервале [ a, b ]. 1. Свойства определенного интеграла Ниже предполагается, что f (x) и g (x) - непрерывные функции на замкнутом интервале [ a, b ]. 1. 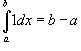 2. 2. 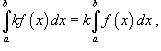 где k - константа; 3. где k - константа; 3. 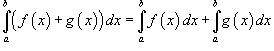 4. 4. 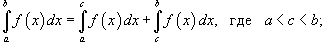 5. Если 5. Если 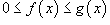 для всех для всех 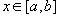 , то , то 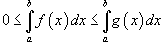 . 6. . 6. 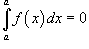 7. 7. 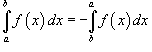 8. Если 8. Если 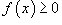 в интервале [ a, b ], то в интервале [ a, b ], то 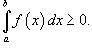 Формула Ньютона-Лейбница Пусть функция f (x) непрерывна на замкнутом интервале [ a, b ]. Если F (x) - первообразная функции f (x) на[ a, b ], то Формула Ньютона-Лейбница Пусть функция f (x) непрерывна на замкнутом интервале [ a, b ]. Если F (x) - первообразная функции f (x) на[ a, b ], то 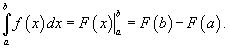 Площадь криволинейной трапеции Площадь фигуры, ограниченной осью 0 x, двумя вертикальными прямыми x = a, x = b и графиком функции f (x) (рисунок 1), определяется по формуле Площадь криволинейной трапеции Площадь фигуры, ограниченной осью 0 x, двумя вертикальными прямыми x = a, x = b и графиком функции f (x) (рисунок 1), определяется по формуле 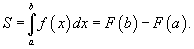
| ||||||
| Пример 1 | ||||||
Вычислить интеграл 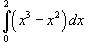 . Решение. Применяя формулу Ньютона-Лейбница, получаем . Решение. Применяя формулу Ньютона-Лейбница, получаем 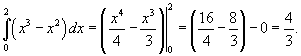 | ||||||
| Пример 2 | ||||||
Вычислить интеграл 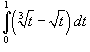 . Решение. . Решение. 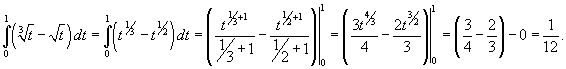 |
https://www.math24.ru/definite-integral.html
 2015-02-04
2015-02-04 1906
1906