Основные формулы дифференцирования

Пусть С – действительное число, U=U(x) и υ= υ(x) – дифференцируемые функции.
1. (С)' =0;
2. (С∙ υ) ' = С υ ';
3. (U± υ) ' = U'± υ '
4. (U ·υ) ' = U' υ +U υ ';
5. .
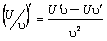Есл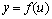и и 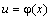, то у называется сложной функцией от х. Есл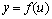и и 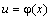дифференцируемы, то 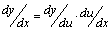или .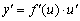

Таблица производных

1..(Uⁿ) '= n· U^n– ¹ · U'.
Следствие: (х) ' =1.

2. (a^u) '=a^u· ln a· U'.
Следствие: (е^u) ' = e^uu'.

3. .
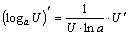Следствие: .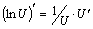

4. (sin U) '= cos U·U'.
5. (cos U) ' =–sin U·U'.
6. .
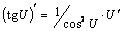7. .
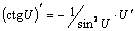8. .
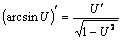9. .
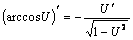10. .
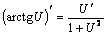11. .
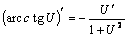Пример. Найти производные заданных функций:
1) .
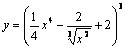Решение. Применим формулу 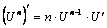, здесь n =3, 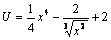. Тогда .
Найдем U'.

Следовательно, .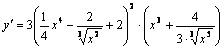
2) .
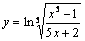Решение. Преобразуем сначала данную функцию, а затем найдем производную этой функции:
.
Тогда .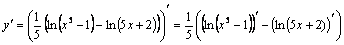
Для нахождения производных 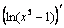и 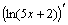применим формулу: .
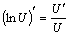Получим:

https://math.immf.ru/lections/006.html

6 7 8 9 10 11 12