¦(x) ® min, (7.17
gi (x) = 0, i = 1: l, (7.18)
gi (x) ≤ 0, i = (l +1): m, (7.19)
где все функции ¦, g 1, g 2,…, gm предполагаются определенными на Еn. Если точка минимума (локального или глобального) лежит на границе допустимого множества, определяемого записанной выше системой неравенств из (7.18), (7.19), то градиент целевой функции не обязательно равен нулевому вектору, т.е.
Ѧ(x) ¹ 0n.
Это означает, что для задач оптимизации с ограничениями условия оптимальности (теорема 4.1 и 4.2) непригодны.
При решении задач условной оптимизации ограничения учитывают, вводя обобщенную функцию Лагранжа переменных х и l.
L (x, λ, λ0) = l0 ¦(x) + 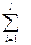 l i gi (x) +
l i gi (x) + 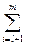 l i gi (x), (7.20)
l i gi (x), (7.20)
где l0, l1, l2,…, l m – множители Лагранжа, которые составляют вектор, обозначаемый l Î Еm.
Функция вида
L (x, λ) = ¦(x) + 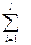 l i gi (x) +
l i gi (x) + 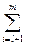 l i gi (x) (7.21)
l i gi (x) (7.21)
называется классической функцией Лагранжа.
Теорема 7.2. (необходимые условия минимума).
Если x * – точка локального минимума в задаче (7.17) … (7.19), то существуют множители Лагранжа l i не равные одновременно нулю, т.е. å l i 2 ¹ 0 и такие, что выполнены условия:
а) стационарности Ñ x L (x, l) = 0n или, что то же самое
Ñ x ¦(x *) + 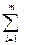 l i Ñ gi (x *) = 0n; (7.22)
l i Ñ gi (x *) = 0n; (7.22)
б) дополняющей нежесткости
l i gi (x *) = 0, i = 1: m; (7.23)
Из условия дополняющей нежесткости следует, что если ограничение неравенство в точке х * пассивное, т.е. gi (x *) < 0, то l i = 0, а если – активное, т.е. – gi (x *) = 0, то l i ≥ 0 (для минимума) и l i ≤ 0 (для максимума).
в) неотрицательности (согласования знаков)
l i ³ 0, i = 1: m; (7.24)
г) допустимости решения
gi (x *) = 0, i = 1: l; gi (x*) ≤ 0, i = (l +1): m. (7.25)
Теорема дополняющей нежесткости и неотрицательности записываются только для ограничений – неравенств. Условие допустимости решения включено для удобства формирования алгоритма решения.
Заметим, что множители Лагранжа, отвечающие ограничениям – равенствам, могут быть положительными, отрицательными или же равными нулю, тогда как множители, которые соответствуют ограничениям – неравенствам, отрицательными быть не должны.
При решении задачи в силу ее линейности по l отдельно рассматриваются случаи λ0 ¹ 0 (регулярный) и λ0 = 0 (нерегулярный). В первом случае можно положить λ0 = 1 или любой другой положительной константе. В задаче на минимум λ0 = -1 или любой другой отрицательной константе в задаче на максимум.
При решении задач проверка условия регулярности затруднена, так как точка х * заранее не известна. Поэтому, как правило, рассматриваются два случая: λ0 = 0 и λ0 ¹ 0. Если λ0 ¹ 0, то в системе (7.20) полагают λ0 = 1. Случай λ0 = 0 отражает вырожденность ограничений. При этом обобщенная функция Лагранжа становится классической (7.24).
Условие gi (x *) £ 0, i = (l +1): m очевидно: точка минимума x * должна удовлетворять исходным ограничениям, т.е. быть допустимой. Равенство (7.22) аналогично равенству (4.5) из теоремы (4.1), где вместо ¦ использована функция Лагранжа. Согласно равенствам (7.20) те множители Лагранжа, которые соответствуют неактивным в точке x* ограничениям, должны обращаться в нуль.
Среди перечисленных условий основным является равенство (7.19). Если все ограничения в точке x * неактивны, то из (7.23) следует, что l1 = l2 =…=l m = 0 и условие (7.22) превращается в условие (4.5). Это говорит о том, что в рассматриваемом случае l1 = l2 =…= l m = 0 ограничения фактически не учитываются и необходимым условием локального минимума в такой точке является равенство градиента целевой функции нулевому вектору.
Теорема 7.3. (достаточные условия минимума (максимума) первого порядка). Пусть имеется точка (х *, λ*), удовлетворяющая системе (7.22…7.25) при λ0* ≠ 0, суммарное число активных ограничений-неравенств в точке 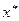 и ограничений-равенств совпадает с числом n переменных (при этом условие регулярности выполняется). Если λ i * > 0 для всех
и ограничений-равенств совпадает с числом n переменных (при этом условие регулярности выполняется). Если λ i * > 0 для всех 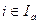 , то точка
, то точка 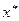 – точка условного локального минимума в задаче (7.1…7.3). Если λ i * < 0 для всех
– точка условного локального минимума в задаче (7.1…7.3). Если λ i * < 0 для всех 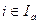 , то точка х * – точка условного локального максимума, где
, то точка х * – точка условного локального максимума, где 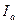 – множество индексов ограничений, активных в точке х *.
– множество индексов ограничений, активных в точке х *.
Теорема 7.4. (необходимые условия минимума (максимума) второго порядка). Пусть 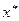 – регулярная точка минимума (максимума) в задаче (7.1 … 7.3) и имеется решение (х *, λ*) системы (7.22…7.25). Тогда второй дифференциал классической функции Лагранжа, вычисленной в точке (х *, λ*), неотрицателен (неположителен):
– регулярная точка минимума (максимума) в задаче (7.1 … 7.3) и имеется решение (х *, λ*) системы (7.22…7.25). Тогда второй дифференциал классической функции Лагранжа, вычисленной в точке (х *, λ*), неотрицателен (неположителен):
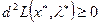 ,
, 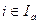
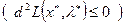
для всех ненулевых 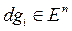 таких, что
таких, что
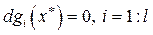 и λ i * > 0 (λ i * < 0);
и λ i * > 0 (λ i * < 0); 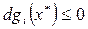 ,
, 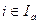 , λ i * = 0.
, λ i * = 0.
Теорема 7.5. (достаточные условия экстремума второго порядка). Пусть имеется точка (х *, λ*), удовлетворяющая системе (7.22…7.25) при λ0* ≠ 0. Если в этой точке
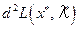 > 0 (
> 0 (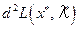 < 0)
< 0)
для всех ненулевых 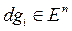 таких, что
таких, что
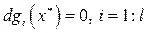 и
и 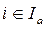 , λ i *> 0 (λ i *< 0);
, λ i *> 0 (λ i *< 0);
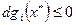 ,
, 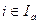 , λ i * = 0,
, λ i * = 0,
то точка 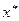 является точкой локального минимума (максимума) в задаче (7.17…7.19).
является точкой локального минимума (максимума) в задаче (7.17…7.19).
 2015-02-04
2015-02-04 953
953