Алгоритм решения задачи

Шаг 1. Составить обобщенную функцию Лагранжа:

L (x, λ, λ₀) = l₀ ¦(x) + 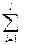l _i g _i (x) + 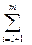l _i g _i (x)

Шаг 2. Записать необходимые условия минимума (максимума) первого порядка:

1) ;

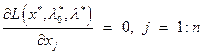2) ;

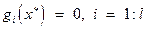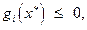
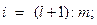
3) 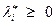, 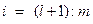(для минимума), 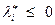, 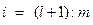(для максимума);

4) .

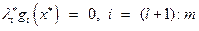Шаг 3. Решить систему для двух случаев:

1) ;

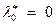2) 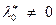(при этом поделить условия, стоящие выше, т.е.1), 3), 4), на 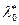и заменить 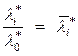). В результате найти условно-стационарные точки х *, выделив из них полученные при 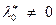(они могут быть регулярными точками экстремума). В каждом из двух случаев следует начинать с рассмотрения 2 ^{m -l} вариантов удовлетворения условия «г» дополняющей нежесткости.

Шаг 4. Для выделенных на шаге 3 точек проверить достаточные условия экстремума первого или второго порядка.

Для проверки достаточных условий первого порядка следует:

1) определить число k ограничений-равенств и активных ограничений неравенств;

2) если k = n и 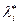> 0для всех 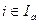, т.е. для всех активных ограничений-неравенств, то в точке 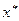– локальный минимум. Если k = n и 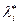< 0 для всех 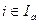, то в точке х *– локальный максимум. Если k < n или соответствующие множители Лагранжа не удовлетворяют достаточным условиям первого порядка, проверить достаточные условия второго порядка.

Для проверки достаточных условий второго порядка следует:

1) записать выражение для второго дифференциала классической функции Лагранжа в точке :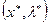

;

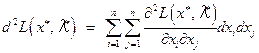2) записать условия, накладываемые на первые дифференциалы ограничений-равенств и активных в точке 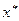ограничений -неравенств:

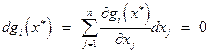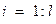, и 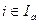, λ _i * > 0 (λ _i * < 0), (7.26)

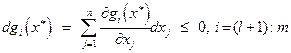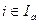, , λ _i * = 0;

3) исследовать знак второго дифференциала функции Лагранжа для ненулевых 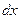, удовлетворяющих (7.26). Если 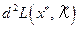> 0, то в точке х * – условный локальный минимум. Если 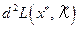< 0, то в точке х * – условный локальный максимум. Если достаточные условия экстремума не выполняются, следует проверить выполнение необходимых условий второго порядка, следуя аналогичной процедуре. Если они выполняются, то требуется дополнительное исследование, а если нет, то в точке 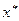нет условного экстремума.

Шаг 5. Вычислить значение функции в точках условного экстремума.

Условия экстремума в задаче (7.17)…(7.19) приведены в табл. 7.1, 7.2.

Таблица 7.1

Необходимые и достаточные условия первого порядка в задаче поиска условного

экстремума при смешанных ограничениях

Необходимые условия первого порядка	Достаточные условия первого порядка
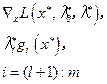
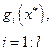
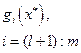
№ п/п				λ0*≥0, λ i *	Число l огра-ничений-равен-ств и активных ограничений-неравенств		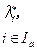Тип условно-стационарной точки
			≤0	≤0	N	>0	Условный локаль-ный минимум
			≤0	≤0	N	<0	Условный локаль ный максимум

Таблица 7.2

Необходимые и достаточные условия второго порядка в задаче поиска условного

экстремума при смешенных ограничениях.

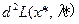
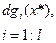
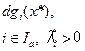
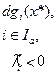
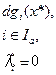
№ п/п						Тип условно-стационарной точки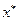
	>0	0,	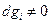0,	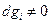	≤0	Условный локальный минимум
	<0	0,	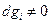	0,	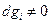≤0	Условный локальный максимум
	≥0				≤0	Может быть условный локаль-ный минимум, требуется дополнительное исследование
	≤0				≤0	Может быть условный локальный максимум, требуется дополнительное исследование
	=0				≤0	Требуется дополнительное исследование
	=0				≤0	Требуется дополнительное исследование
	≠0				≤0	Нет эктремума
	≠0				≤0	Нет экстремума

Пример 7.10. Износ периферийного оборудования ЭВМ зависит от количества выполненных вычислений, причем различные типы оборудования имеют разный износ.

Функция износа одного типа оборудования описывается полиномом

И₁(х ₁) = а ₁ х ₁ + а ₂ х ₁²,

где а ₁, а ₂ – известные коэффициенты; х ₁ – вычислительная продукция, полученная на первом оборудовании.

Функция износа второго оборудования имеет квадратичную зависимость от количества х ₂ выполненных вычислений:

И₂(х ₂) = а ₃ х ₂²,

где а ₃ – известный коэффициент.

Всего вычислительной продукции выдается n= х ₁ + х ₂. Требуется так распределить работу оборудования, чтобы вся вычислительная продукция была получена при минимальном общем износе оборудования.

Решение. Целевой функцией является

f (x) = а ₁ х ₁ + а ₂ х ₁² + а ₃ х ₂².

Эту функцию нужно минимизировать при ограничении - равенстве

П = х ₁ + х ₂,

где П – известная положительная величина.

Составим функцию Лагранжа

L (x, λ) = а ₁ х ₁ + а ₂ х ₁² + а ₃ х ₂² + λ(П - х ₁ - х ₂).

Для отыскания оптимального решения запишем частные производные от функции Лагранжа по всем переменным:

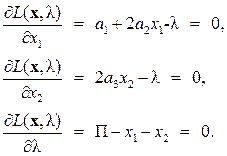
В итоге имеем систему трех уравнений с тремя неизвестными. Решая систему, получим:

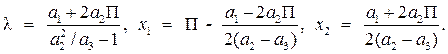
Пример. Предпочтения потребителя заданы в виде функции

,

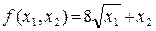где х ₁ и х ₂ – объемы потребления 1-го и 2-го товаров соответственно. Доход равен 70 отн. ед. Цены 1-го и 2-го товаров соответственно равны Ц₁ = 1, Ц₂ =2. Найти оптимальный набор потребительских товаров.

Решение. Используем метод штрафных функций и составим обобщенную функцию

f (x, k) = 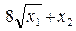+ k (Ц₁ х ₁ + Ц₂ х ₂ – 70)².

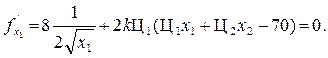
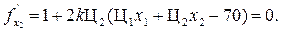
Решая, полученные уравнения, получим х ₁ = 64, х ₂ = 3.