Постановка задачи нелинейного программирования и ее геометрическая интерпретация

Задача нелинейного программирования формулируется следующим образом:

определить минимальное значение функции

f (x) → min (7.1)

при условии, что её переменные удовлетворяют соотношениям

g_i (x) = b_i, i = 1: l, (7.2)

g_i (x) £ b_i, i = (l +1): m, (7.3)

где f (x), g_i (x), i = 1: m − некоторые известные функции (необязательно линейные) n переменных, а b_i − заданные числа. Считаем, что все функции f_i (x), g_i (x), i = 1: m определены на некотором открытом множестве X 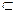Eⁿ. Для упрощения ограничимся случаем Х = Еⁿ.

Условие неотрицательности переменных x_j ³ 0, j = 1: n, входящее в постановки многих задач нелинейного программирования, можно записать в виде неравенств (7.3), положив g_j (x) = - x_j, b_j = 0.

В евклидовом пространстве Eⁿ система ограничений (7.2) … (7.3) определяет область допустимых решений задачи. В отличие от задачи линейного программирования она не всегда является выпуклой.

Cформулированная задача (7.1) … (7.3) представляет собой частный случай общей задачи математического программирования, заключающийся в определении наименьшего значения целевой функции f (x) на допустимом множестве

Х = { х 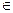Х | g_i (х) = b_i, i = 1: l, g_i (х) ≤ b_i, i = (l +1): m }.

Отметим, что если все функции g_i (х) непрерывны в Еⁿ, то множество Х замкнуто.

Большинство известных методов решения задачи нелинейного программирования позволяют найти лишь точки локального минимума целевой функции на заданном множестве. В этой связи важную роль играет априорная информация о существовании решения задачи, т.е. информация о том, достигает ли целевая функция наименьшего значения на допустимом множестве. В частности, если множество Х ограничено, а целевая функция непрерывна на Х, то задача нелинейного программирования имеет решение.

Однако проверить ограниченность множества Х не просто. Поэтому интересны другие условия, налагаемые на целевую функцию и ограничения и позволяющие делать заключение о существовании решения без использования ограниченности допустимого множества. В задаче выпуклого программирования, в которой целевая функция выпукла и допустимое множество Х выпукло, любая точка локального минимума целевой функции, согласно утверждения 3.1, является решением этой задачи.

Если определена область допустимых решений, то нахождение решения задачи (7.1) … (7.3) сводится к определению такой точки этой области, через которую проходит гиперплоскость наинизшего уровня: f (x) = α, где α − произвольное число.

Процесс нахождения решения задач нелинейного программирования (7.1)…(7.3) с использованием её геометрической интерпретации включает следующие этапы:

1. Находят область допустимых решений задачи, определяемую соотношениями (7.2) … (7.3).

2. Строят гиперплоскость f (x) = α.

3. Определяют гиперплоскость наинизшего уровня или устанавливают неразрешимость задачи из-за неограниченности функции (7.1) снизу на множестве допустимых решений.

4. Находят точку области допустимых решений, через которую проходит гиперплоскость наинизшего уровня, и определяют в ней значение функции (7.1).

Пример 7.1. Найти максимальное значение функции

f (х) = x ₂ − x ₁² + 6 x ₁ (7.4)

при условиях

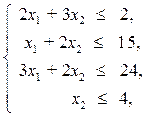(7.5)

x ₁, x ₂ ³ 0. (7.6)

Решение. Так как целевая функция (7.4) нелинейная, то задача (7.4) … (7.6) является задачей нелинейного программирования. Областью допустимых решений данной задачи является многоугольник 0 АВС (рис. 7.4). Следовательно, для нахождения её решения нужно определить такую точку многоугольника 0 АВС, в которой функция (7.4) принимает максимальное значение. Построим линию уровня f (х) = x ₂ − x ₁² + 6 x ₁ = α, где α – некоторая постоянная, и исследуем её поведение при различных значениях α.. При каждом значении α получаем параболу, которая чем дальше отдалена от оси 0 x ₁, тем больше значение α.. Значит, функция f принимает максимальное значение в точке касания одной из парабол с границей многоугольника 0 АВС. В данном случае это точка D (рис. 7.4), в которой линия уравнения f = x ₂ − x ₁² + 6 x ₁ = 13 касается стороны АВ многоугольника 0 АВС.

Координаты точки D можно найти из системы уравнений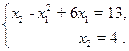

Решая эту систему, получим x ₁^* = 3; x ₂^* = 4. Итак, f _max = 13 при x ^* (3;4).

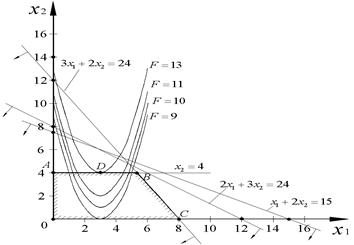
Рис. 7.4. Область допустимых решений

Для нахождения гиперплоскости наинизшего уровня можно руководствоваться следующими соотношениями: точка x ^* = (x _{1 min}, x _{2 min}) принадлежит прямой x ₂ = 0 и параболе f _min = x ₂ − x ₁² +6 x ₁ , а потому обоим этим уравнениям, т. е. может быть определена как решение системы

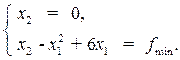(7.7)

Однако, так как нам не известно f * − оптимальное значение целевой функции f (x ₁, x ₂), то в этой системе оказывается три переменных и всего два уравнения, поэтому систему необходимо дополнить ещё одним уравнением, связывающим переменные x ₁, x ₂, f _min.

Нужное уравнение можно получить, если учесть, что угловой коэффициент касательной к параболе, по которой целевая функция достигает своего минимального значения, равен 1: касательной в этой точке является прямая x ₂ = 0. Как мы знаем, угловой коэффициент касательной к кривой x ₂ = f (x ₁) в точке x ₁ равен ∂ x ₂ / ∂ x ₁. Поэтому в нашем случае имеем

∂ x ₂ / ∂ x ₁ = 0. (7.8)

Вычислим теперь производную целевой функции f _min. Для этого продифференцируем левую и правую часть этого соотношения по x ₁. Получим:

0 = 0 − 2 x ₁ + 6. (7.9)

Первое слагаемое дифференцируем, как сложную функцию от x ₂:

∂[ x ₂]/∂ x ₁ = ∂[ x ₂]/∂ x ₂·∂ x ₂/∂ x ₁ = 0.

Откуда из (7.9) следует 0 = 2 x ₁ +6. Если учесть (7.8), то окончательно получим:

2 x ₁ − 6 = 0, x ₁ = 3.

Дополняя этим последним соотношением систему (7.7), окончательно получим:

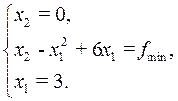
Откуда −9 + 18 = f *, f * = 9.

Для нахождения максимального значения функции поступаем аналогичным образом. Получаем систему:

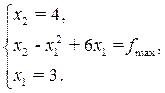
Решая её, получим f _max = 13.

Рассмотрим задачу нелинейного программирования, в которой все ограничения заданы линейными функциями, на переменные x ₁,…, x_n наложены условия неотрицательности, а целевая функция нелинейная.