2015-02-04
951
Таблица 2.4
Распределение рабочих завода по уровню месячной заработной платы
| Заработная плата, т. р. | Число рабочих, чел | Проценты к итогу |
| признак (х) | частота (f) | частость (f) |
| .................... | ...................... | ...................... |
 350 - 450
| 48,0 | |
| варианта | ||
| ...................... | ...................... | ...................... |
| В С Е Г О: | 180 (объем ряда распределения) | 100,0 |
В данной таблице уровень заработной платы является вариантой, а число рабочих - частотой, показывающей, сколько раз повторяется данная варианта (т.е. сколько рабочих получают заработную плату, лежащую в пределах от 350 до 450 тыс. руб.). Частота, выраженная в процентах (в данном примере - 48,0) - это частость. Сумма всех частот называется объемом ряда распределения или его численностью (в данном случае было обследовано 180 рабочих).
Вариация признака может быть дискретной (прерывной) или непрерывной. При дискретной вариации признака значение вариантов отличается друг от друга на вполне определенную величину, и варианты обычно выражаются целыми числами (например, число членов семьи - 1, 2, 3, 4 и т. д.). Такие ряды называются вариационными дискретными рядами.
При непрерывной вариации признака его величина может принимать любые значения в определенном интервале (интервальные ряды распределения), например, рост человека, урожайность, заработная плата и т.д. Построение интервального ряда основано на принципах статистической группировки.
Интервалы могут быть неравными, поэтому сравнивать частоты и судить о степени заполнения разных интервалов нельзя. В целях сравнения заполненности интервалов рассчитывается показатель, называемый плотностью распределения, - т.е. число единиц совокупности, приходящееся в среднем на одну единицу ширины интервала (ширина интервала - разность между его границами). Если плотность определяется с помощью частот, она называется абсолютной, если с помощью частостей - относительной.
Для облегчения анализа рядов распределения их изображают при помощи графиков.
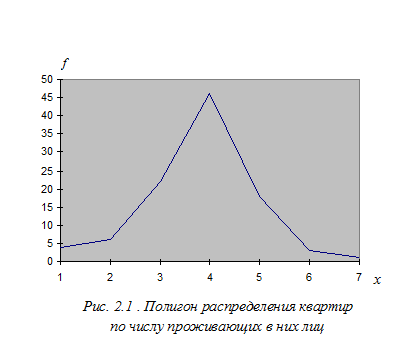
При дискретной вариации анализа признака графиком вариационного ряда служит полигон распределения. Он представляет собой замкнутый многоугольник, абсциссами вершин которого являются значения варьирующего признака, а ординатами - соответствующие им частоты или частости. Для примера рассмотрим построение полигона распределения по следующим данным (таблица 2.5). Полигон распределения приведен на рис.2.1.
Таблица 2.5
Распределение квартир жилого дома по числу проживающих в них лиц
| Число лиц, живущих в квартире, x | Всего | |||||||
| Число квартир, f | ||||||||
| Накопленные частоты |
Для иллюстрации рядов распределения часто используется кумулятивная кривая или кумулята, построенная по накопленным частотам. Накопленная частота показывает, какое число единиц имеет величину варианта не большую данной и находится путем последовательного суммирования частот (строка 3 в табл.2.5), например из табл.2.5 видно, что в 10 квартирах проживают семьи, состав которых не превышает 2 человек, в 78 квартирах проживают семьи, состав которых не превышает 4 человек и т. д. Кумулята приведена на рис.2.2.
Если при построении кумуляты поменять местами значения признака и частоты (т.е. на оси ординат отложить значения признака, а на оси абсцисс - частоты) то получим кривую, называемую огивой.
Для иллюстрации интервального ряда распределения применяют график, называемый гистограммой распределения. Гистограмма представляет собой ряд смежных столбиков, основание каждого равно величине соответствующего интервала, а высота - частоте (правильнее - пропорциональна частоте). Пример гистограммы приведен на рис.2.3.
 |
Разновидностью кумулятивной кривой является график Лоренца или кривая концентрации. Например, необходимо дать характеристику уровня концентрации производства в промышленности России по числу рабочих (см. табл. 2.6). График приведен на рис. 2.4. Если бы численность рабочих распределялась равномерно по числу предприятий, т.е. процесс концентрации отсутствовал полностью, график представлял бы собой прямую линию. При неравномерном распределении линия концентрации отходит от прямой, причем, чем выше уровень концентрации, тем больше ее кривизна.
 |
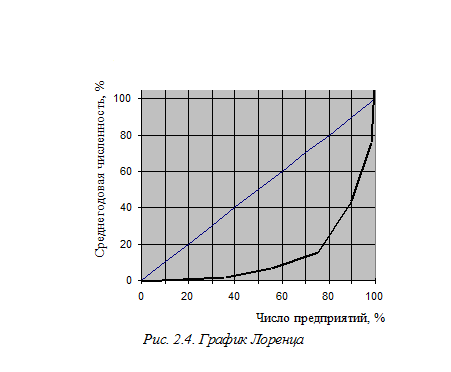Таблица 2.6
Группировка промышленных предприятий по численности
рабочих за 20__г.
| Группы предприятий по числу рабочих, чел | Число предприятий | Среднегодовая численность | ||
| % к итогу | кумулятивные итоги | % к итогу | кумулятивные итоги | |
| до 100 | 35,00 | 35,0 | 3,3 | 3,3 |
| 101-200 | 19,6 | 54,6 | 5,4 | 8,7 |
| 201-500 | 22,9 | 77,5 | 14,2 | 22,9 |
| 501-1000 | 11,3 | 88,8 | 15,3 | 38,2 |
| 1001-3000 | 8,4 | 97,2 | 26,8 | 65,0 |
| 3001-10000 | 2,5 | 99,7 | 23,6 | 88,6 |
| 10001 и более | 0,3 | 100,0 | 11,4 | 100,0 |
РАЗДЕЛ 3. АБСОЛЮТНЫЕ И ОТНОСИТЕЛЬНЫЕ ВЕЛИЧИНЫ
3.1. Абсолютные величины
Абсолютной величиной называется статистический показатель, выражающий абсолютные размеры изучаемого явления.
По способу выражения размеров изучаемых явлений абсолютные величины подразделяются на индивидуальные, которые отражают абсолютные размеры каждой отдельной единицы совокупности, и суммарные (групповые), которые получаются суммированием индивидуальных абсолютных величин.
Абсолютные величины - всегда числа именованные, имеющие определенную размерность, единицу измерения. В зависимости от различных причин и целей анализа применяют натуральные, условно-натуральные, трудовые и стоимостные единицы измерения.
Натуральные измерители в большинстве своем соответствуют природным или потребительским свойствам предмета изучения и выражаются в физических мерах веса, длины и т. д. Учет в натуральных единицах измерения называется натуральным учетом. Иногда применяется составная единица измерения (например, тоннокилометры - ткм и т. д.).
Однородная, но неодинаковая продукция измеряется в условно-натуральных единицах измерения. Такие единицы получают, приводя различные натуральные единицы к одной, принятой за базу, например, в консервной продукции емкость банки в 354,4 см3 принята за условную и вся продукция пересчитывается в этих условных банках. Аналогично производится пересчет в условно-натуральные измерители и в других отраслях (топливной, текстильной и пр.).
Показатели, отражающие результаты труда, измеряются в трудовых единицах измерения, а наиболее распространенные – в стоимостных (или денежных) единицах измерения.
3.2. Относительные величины:
сущность, виды, единицы измерения
Статистические показатели, выражающие относительные размеры изучаемого явления, называются относительными величинами.
Относительные величины получаются в результате деления одной величины на другую, принимаемую за базу сравнения (или основание относительной величины). Причем следует иметь в виду, что в числителе всегда находится показатель, отражающий то явление, которое изучает, т.е. сравнимый показатель, а в знаменателе - показатель, с которым производится сравнение.
База сравнения выступает в качестве своеобразного измерителя. Если значение базы принимается за единицу (производится простое деление двух величин), то относительная величина выражается в коэффициенте (например, темпы роста), если основание (база) - 100%, то относительная величина выражается в процентах.
Иногда за базу принимают 1000 (при расчете коэффициентов рождаемости или смертности, естественного или механического прироста показателя, в фармации и т. д.). Такие единицы измерения называются промилле и обозначаются %0.
Все относительные величины делятся на относительные величины выполнения плана и планового задания (в настоящее время лучше говорить о выполнении договорных обязательств), динамики, структуры, координации, интенсивности, сравнения, уровня экономического развития.
Относительная величина выполнения плана (ОВВП) - соотношение величины показателя, достигнутое за какое-то время или какому-либо моменту, и величины его, установленной по плану за это же время:
| Факт (2008) |
| План (2008) |
ОВВП =
- факт (2008) - фактическое выполнение за 2008 г.;
- план (2008) - плановое значение за 2008 г.
| План(2008) |
Относительная величина планового задания (ОВПЗ) - соотношение плановой величины показателя к его фактически достигнутому уровню в предыдущем периоде (или в периоде, принятом за базу):
 ОВПЗ=
|
| Факт (2007) |
- факт (2007) - фактическое выполнение за 2007 г.
Произведение этих двух величин дает относительную величину динамики (см. ниже): ОВД = ОВВП × ОВПЗ;
Относительная величина динамики (ОВД) - соотношение величины показателя за данное время и величины его за какое-либо аналогичное предшествующее время, принятое за базу сравнения. Относительная величина динамики характеризует степень, скорость изменения показателя во времени, в частности, темпы роста. Она выражается в виде краткого отношения (коэффициента) или в процентах. Если имеется ряд динамики (ряд во времени) абсолютных величин, то ОВД может исчисляться как отношение величины показателя за каждое последующее время к величине его за непосредственно предшествующее ему время или как отношение к величине его за одно и то же время, принятое за базу сравнения. В первом случае относительная величина динамики называется ОВД с переменной базой или цепная, во втором - с постоянной базой сравнения или базисная.
Если уровни ряда обозначить через Y i , то ОВД вида:
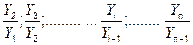называются цепными, а вида:
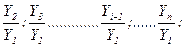базисными (более подробно эта тема раскрывается в разделе рядов динамики).
Относительная величина структуры характеризует состав изучаемой совокупности и показывает какой удельный вес (какую долю) в общем итоге составляет каждая ее часть. Она получается в результате деления значения каждой части совокупности на их общий итог, принятой за базу.
Относительная величина координации характеризует соотношение отдельных частей целого, одна из которых принимается за базу сравнения и является дополнением к относительной величине структуры. Например, число сельских жителей, приходящихся на 100 городских и т. д.
Относительная величина интенсивности (степени) показывает степень распространенности данного явления в определенной среде. Обычно это отношение двух разноименных абсолютных величин (плотность населения на квадратный километр; производство сельскохозяйственной продукции на 1 га сельхозугодий и пр.).
Относительная величина сравнения характеризуют соотношение одноименных показателей, относящихся к различным объектам или территориям, но за один и тот же период времени.
Относительная величина уровня экономического развития – обычно соотношение величины важнейших экономических показателей (страны, региона, отрасли) и численности населения (так называемые показатели на душу населения).
