2015-02-04
682
Получим наиболее общее уравнение, связывающее поверхностные и массовые силы так называемое уравнение движения в напряжениях. Для вывода уравнения проанализируем движение жидкой частицы, масса которой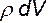 
и поверхность dS. Аналогично тому, как это было сделано для тетраэдра, можем записать уравнение движения в виде
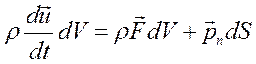(2.11)
Для всего движущегося объема (V), поверхность которого S, имеем
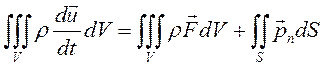(2.12)
Преобразуем поверхностный интеграл в правой части в объемный с учетом того, что, как было показано, тензор напряжений имеет вид
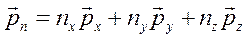
где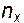 
, 
, 
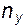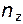- направляющие косинусы.
Воспользуемся известными из векторного анализа и справедливыми для любых векторов формулами:
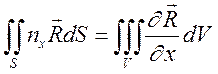
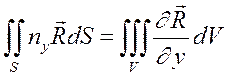; (2.13)
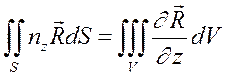
Применяя эти формулы к тензору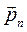 
, получаем:
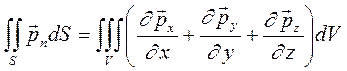(2.14)
Подставляя это выражение в исходное уравнение, получаем:
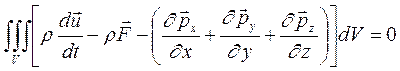
Но так как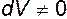 
, а объем V выбран произвольно, то
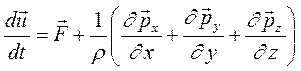(2.15)
Это и есть уравнение движения в напряжениях.
В проекциях на декартовы оси координат можем записать:
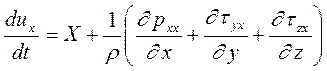
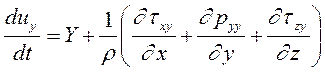(2.16)
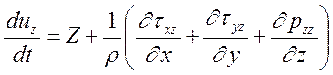
Эта система включает в качестве неизвестных девять величин: три проекции скорости и шесть проекций напряжений. Проекции единичных массовых сил, как правило, известны из постановки задачи.
Лекция №7
