Поток векторного поля

Пусть dS (рис. 1.1) - элемент поверхности, а 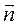- единичный вектор, направленный по внешней нормали. Потоком векторного поля (например, 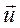) называют поверхностный интеграл вида

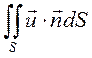(1.10)

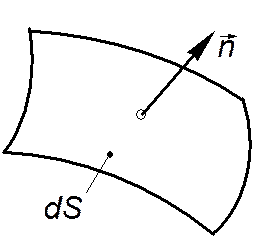
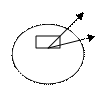
Рис. 1.1

Изменение массы объема происходит за счет вытекания(втекания)

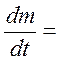jdS

Изменение массы можно выразить через изменение объема

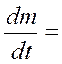r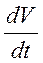

Изменение массы в объеме эквивалентно потоку жидкости, покидающему объем через поверхность, ограничивающую объем

Интегральный баланс имеет вид

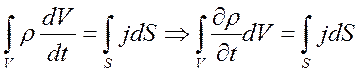(1)

рассмотрим баланс для элемента объема

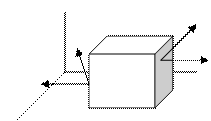
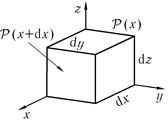
dv = dxdydz

–элементарный объем

Определим суммарный поток через поверхность как сумму элементарных потоков

Изменение потока вектора а в направлении оси абсцисс

dI = - a_xdydz + a_x+dxdydz

Используем разложение в ряд Тейлора для компоненты вектора а для правой плоскости

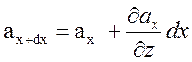
подставляя это разложение, получим для изменения потока

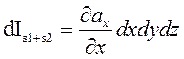
Аналогично для других плоскостей

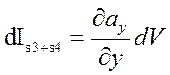
3)

=

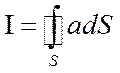
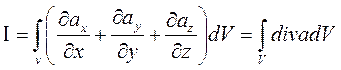
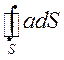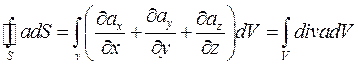
- Теорема Остроградского – Гаусса: