Система уравнений Максвелла в дифференциальной форме

Применяя теорему Стокса можно преобразовать интеграл по замкнутому контуру l в интеграл по поверхности S, натянутой на этот контур.

Теорема Остроградского-Гаусса позволяет преобразовать интеграл по замкнутой поверхности S в интеграл по объему, ограниченному этой поверхностью. Преобразовав левые части уравнений (13.3) можно получить систему Максвелла в дифференциальной форме:

Первая пара:

,

.

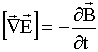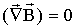Вторая пара:

,

.

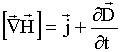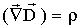Здесь

.

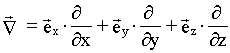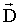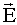К этим уравнениям необходимо добавить закон Ома в дифференциальной форме и связь с , с :

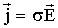
см. (10.5),

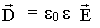
см. (9.13.4),

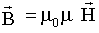
см. (12.5).

Эти три векторных уравнения характеризуют свойства среды. Семь записанных выше уравнений составляют основу электродинамики покоящихся сред.