Доказательство. Пусть q – наименьший отличный от единицы делитель целого a больше единицы

Пусть q – наименьший отличный от единицы делитель целого a больше единицы. Если бы q было бы составным, то оно имело бы некоторый делитель 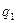с условием 1< 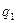< q. Причем число a, делясь на q должно делиться на 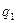. А это бы противоречило допущению относительно того, что q наименьший делитель.