Теорема о движении центра масс системы

Произведение массы системы на ускорение ее центра масс равно геометрической сумме всех действующих на систему внешних сил 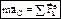– дифференциальное уравнение движения центра масс. В проекциях на оси координат: .

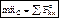Закон сохранения движения центра масс. Если главный вектор (векторная сумма) внешних сил остается все время равным нулю, то центр масс механической системы находится в покое или движется прямолинейно и равномерно. Аналогично в проекциях на оси, если 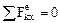Þ 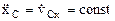, если при этом в начальный момент v_Cx0= 0, то Þ 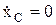Þ x_C= const.

Количество движения системы Q (иногда обозначают К) – вектор, равный геометрической сумме (главному вектору) количеств движения всех точек системы:

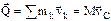, М – масса всей системы, v_C – скорость центра масс.