ГОСУДАРСТВЕННЫЙ МЕДИЦИНСКИЙ УНИВЕРСИТЕТ г. СЕМЕЙ
Методическое пособие по теме:
Исследование реологических свойств биологических жидкостей.
Методы исследования кровообращения.
Реография.
Составитель: Преподаватель
Ковалева Л.В.
Основные вопросы темы:
- Уравнение Бернулли. Статическое и динамическое давления.
- Реологические свойства крови. Вязкость.
- Формула Ньютона.
- Число Рейнольдса.
- Ньютоновская и Неньютоновская жидкость
- Ламинарное течение.
- Турбулентное течение.
- Определение вязкости крови с помощью медицинского вискозиметра.
- Закон Пуазейля.
- Определение скорости кровотока.
- Полное сопротивление тканей организма. Физические основы реографии. Реоэнцефалография
- Физические основы баллистокардиографии.
Уравнение Бернулли. Статическое и динамическое давления.
Идеальной называется несжимаемая и не имеющая внутреннего трения, или вязкости; стационарным или установившимся называется течение, при котором скорости частиц жидкости в каждой точке потока со временем не изменяются. Установившееся течение характеризуют линиями тока - воображаемыми линиями, совпадающими с траекториями частиц. Часть потока жидкости, ограниченная со всех сторон линиями тока, образует трубку тока или струю. Выделим трубку тока настолько узкую, что скорости частиц V в любом ее сечении S, перпендикулярном оси трубки, можно считать одинаковыми по всему сечению. Тогда объем 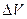 жидкости, протекающий через любое сечение трубки в единицу времени остается постоянным, так как движение частиц в жидкости происходит только вдоль оси трубки:
жидкости, протекающий через любое сечение трубки в единицу времени остается постоянным, так как движение частиц в жидкости происходит только вдоль оси трубки: 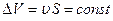 . Это соотношение называется условием неразрывности струи. Отсюда следует, что и для реальной жидкости при установившемся течении по трубе переменного сечения количество Qжидкости, протекающее в единицу времени через любое сечение трубы, остается постоянным (Q = const) и средние скорости течения в различных сечениях трубы обратно пропорциональны площадям этих сечений:
. Это соотношение называется условием неразрывности струи. Отсюда следует, что и для реальной жидкости при установившемся течении по трубе переменного сечения количество Qжидкости, протекающее в единицу времени через любое сечение трубы, остается постоянным (Q = const) и средние скорости течения в различных сечениях трубы обратно пропорциональны площадям этих сечений: 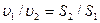 и т. д.
и т. д.
Выделим в потоке идеальной жидкости трубку тока, а в ней — достаточно малый объем жидкости 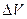 массой
массой 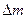 , который при течении жидкости перемещается из положения А в положение В.
, который при течении жидкости перемещается из положения А в положение В.
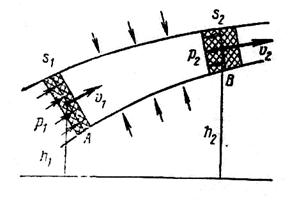 Из-за малости объема можно считать, что все частицы жидкости в нем находятся в равных условиях: в положении А имеют давление
Из-за малости объема можно считать, что все частицы жидкости в нем находятся в равных условиях: в положении А имеют давление 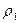 скорость
скорость 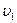 и находятся на высоте h1от нулевого уровня; в положении В — соответственно
и находятся на высоте h1от нулевого уровня; в положении В — соответственно 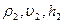 . Сечения трубки тока соответственно S1 и S2.
. Сечения трубки тока соответственно S1 и S2.
Жидкость, находящаяся под давлением, обладает внутренней потенциальной энергией (энергией давления), за счет которой она может совершать работу. Этаэнергия Wp измеряется произведением давления 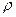 на объем V жидкости:
на объем V жидкости: 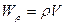 . В данном случае перемещение массы
. В данном случае перемещение массы 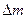 жидкости происходит под действием разности сил давления в сечениях Si и S2. Совершаемая при этом работа Ар равняется разности потенциальных энергий давления в точках
жидкости происходит под действием разности сил давления в сечениях Si и S2. Совершаемая при этом работа Ар равняется разности потенциальных энергий давления в точках 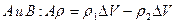 . Эта работа расходуется на работу по преодолению действия силы тяжести
. Эта работа расходуется на работу по преодолению действия силы тяжести 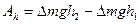 и на изменение кинетической энергии массы
и на изменение кинетической энергии массы
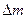 жидкости:
жидкости: 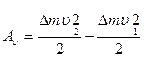
Следовательно, Ар = Ah + AD
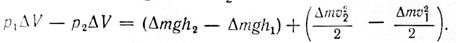
Перегруппировав члены уравнения, получим
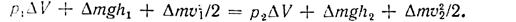
Положения А и В выбраны произвольно, поэтому можно утверждать, что в любом месте вдоль трубки тока сохраняется условие
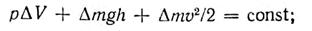
разделив это уравнение на 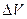 , получим
, получим
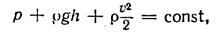
где 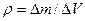 — плотность жидкости.
— плотность жидкости.
Это и есть уравнение Бернулли. Все члены уравнения, как легко убедиться, имеют размерность давления и называются: 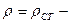 статистическим:
статистическим: 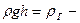 гидростатическим:
гидростатическим: 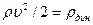 - динамическим. Тогда уравнение Бернулли можно сформулировать так:
- динамическим. Тогда уравнение Бернулли можно сформулировать так:
при стационарном течении идеальной жидкости полное давление равное сумме статического, гидростатического и динамического давлений, остается величиной постоянной в любом поперечном сечении потока.
Для горизонтальной трубки тока гидростатическое давление остается постоянным и может быть отнесено в правую часть уравнения, которое при этом принимает вид
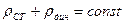
статистическое давление обусловливает потенциальную энергию жидкости (энергию давления), динамическое давление — кинетическую.
Из этого уравнения следует вывод, называемый правилом Бернулли:
статическое давление невязкой жидкости при течении по горизонтальной трубе возрастает там, где скорость ее уменьшается, и наоборот.
 2015-02-04
2015-02-04 15145
15145