Равновесие жидкости. Уравнение равновесия

Если сплошная среда неподвижна (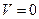) в некоторой инерциальной системе координат, то говорят, что она находится в равновесии. Рассмотрим уравнение движения (1.6.22) полагая, что среда несжимаемая (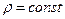) и находится в состоянии равновесия. Согласно закону Ньютона (1.3.6) касательные напряжения в этом случае равны нулю, а нормальные напряжения подчиняются зависимости (1.2.8), тогда:

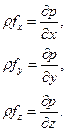(2.1.1)

Система (2.1.1) называется системой дифференциальных уравнений равновесия сплошной среды Эйлера. А 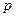- гидростатическим давлением.

Умножая уравнения на 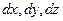соответственно, и складывая их, в соответствии с определением полного дифференциала получим зависимость:

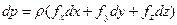. (2.1.2)

Которая называется основным дифференциальным уравнением равновесия жидкости.

Пусть на жидкость действует только сила тяжести, не нарушая общности, направим ее обратно оси , а начало системы координат поместим на дно водоема. Тогда:

.

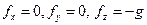А основное уравнение равновесия жидкости (2.1.2) принимает вид:

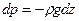. (2.1.3)

Будем понимать под поверхностью уровня – поверхность, на которой значение некой функции постоянно. Пусть в нашем случае это будет давление, тогда поверхность уровня – поверхность равного значения давления.

Проинтегрируем (2.1.3)

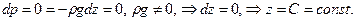(2.1.4)

Следовательно, поверхности уровня – есть семейство плоскостей нормальных направлению силы тяжести. Если поверхность соприкасается с атмосферой и давление на ней равно атмосферному (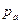), то условимся называть такую поверхность свободной. Плоскость нормальную оси z и проходящую через самую глубокую точку водоема называют плоскостью сравнения.

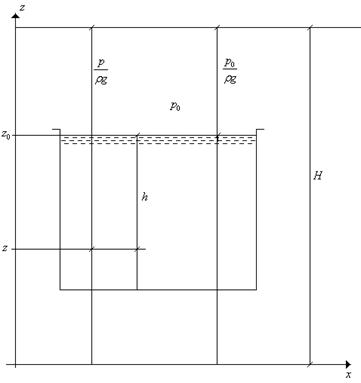
Рис.2.1. Геометрическая интерпретация основного уравнения гидростатики

Запишем (2.1.3) в виде:

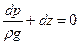. (2.1.5)

Пусть на некой поверхности:

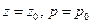. (2.1.6)

Часто за таковую выбирают свободную поверхность. Интегрирование (2.1.5) при граничных условиях (2.1.6) дает распределение гидростатического давления по глубине:

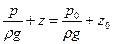. (2.1.7)

Данное уравнение называется основным уравнением гидростатики (первая форма записи). Заметим, что каждый член уравнения имеет размерность длины. Это позволяет ввести величину 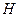называемую гидростатическим (потенциальным) напором, постоянную для каждого конкретного водоема:

.

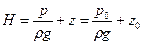Если данное уравнение умножить на 1 Н, то все его члены будут иметь размерность в единицах энергии Дж = Н∙м. А каждое слагаемое представляет собой вид потенциальной энергии, так как жидкость находится в покое: 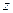- удельная потенциальная энергия положения, 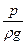- удельная потенциальная энергия давления, 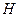- полная удельная потенциальная энергия. Удельная означает в данном случае приходящаяся на единицу веса жидкости 1 Н.

Определение величины гидростатического давления. Перепишем (2.1.7) в виде:

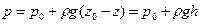. (2.1.8)

Здесь 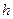- расстояние (по вертикали) от поверхности жидкости до любой произвольной точки внутри, а (2.1.8) также называется основным уравнением гидростатики (вторая форма записи) и позволяет определить величину гидростатического давления в любой точке жидкости. Здесь, 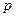- «абсолютное» (полное) давление (величина 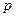всегда положительна 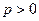); 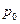- внешнее давление (на поверхности жидкости); - весовое давление. Тогда:

.

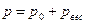Закон Паскаля. Внешнее давление на свободной поверхности жидкости, находящейся в равновесии, передается во все точки жидкости без изменения по всем направлениям.