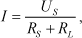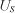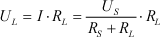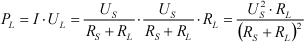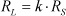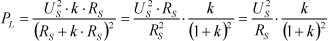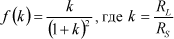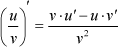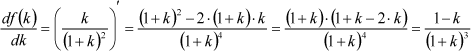| Что такое согласованная нагрузка | |
| В учебной литературе согласование с нагрузкой рассматривается чаще всего применительно к волновым свойствам длинной линии при передаче высокочастотного сигнала. Но в [1] всё же рассмотрены энергетические соотношения при передаче энергии от активного двухполюсника к пассивному. |
| Активный двухполюсник - это любой источник электрической энергии, а пассивный - её потребитель, который чаще всего именуют нагрузкой. Возьмём в качестве активного двухполюсника источник э.д.с. с известным выходным сопротивлением (см. схему на рис.1) и посчитаем, при каком же сопротивлении нагрузки мощность, передаваемая в нагрузку, будет максимальной. |
| |
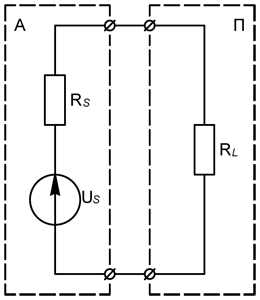 | | Рис.1. | Схема подключения нагрузки к источнику э.д.с. | |
| |
| Согласно закону Ома для полной электрической цепи ток в нагрузке равен: |
| | 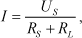 | (1) | | |
| где: |
| | 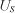 | - напряжение холостого хода активного двухполюсника; | | | 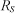 | - выходное сопротивление активного двухполюсника; | | | 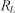 | - сопротивление нагрузки. | |
| |
| Напряжение холостого хода активного двухполюсника измеряется высокоомным вольтметром на зажимах активного двухполюсника при отключенной нагрузке. |
| Напряжение на нагрузке: |
| | 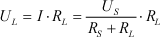 | (2) | | |
| Мощность в нагрузке: |
| | 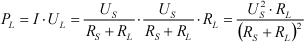 | (3) | | |
Поскольку обе величины 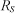 и и 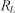 измеряются в омах, выразим для упрощения дальнейших математических выкладок величину измеряются в омах, выразим для упрощения дальнейших математических выкладок величину 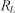 через коэффициент пропорциональности k, показывающий, во сколько раз сопротивление нагрузки через коэффициент пропорциональности k, показывающий, во сколько раз сопротивление нагрузки 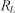 отличается от выходного сопротивления активного двухполюсника отличается от выходного сопротивления активного двухполюсника 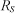 : : |
| | 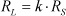 | (4) | | |
| Тогда после подстановки выражение для мощности в нагрузке (3) примет вид: |
| | 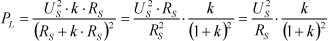 | (5) | | |
| Поскольку левый множитель в последнем выражении - величина постоянная, то максимум мощности в нагрузке совпадёт с максимумом правого множителя, то есть функции: |
| | 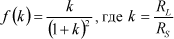 | (6) | | |
| Максимальное значение функция f(k) примет при таком k, при котором будет равна нулю её производная по k. Производная частного двух функций определена как: |
|
| Следовательно: |
| | 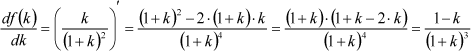 | (7) | | |
Очевидно, что производная принимает нулевое значение лишь при k=1, то есть при выполнении равенства 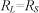 . Максимум мощности в нагрузке при k=1 хорошо виден на графике, приведенном на рис.2: . Максимум мощности в нагрузке при k=1 хорошо виден на графике, приведенном на рис.2: |
| |
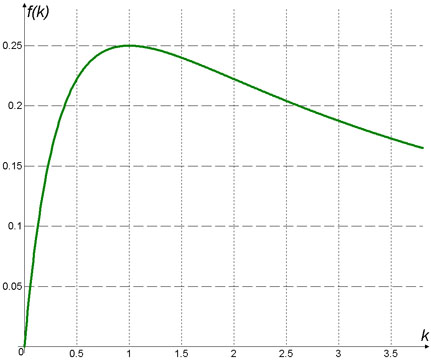 | | Рис.2. | Зависимость мощности в нагрузке от отношения сопротивления нагрузки к выходному сопротивлению активного двухполюсника | |
| |
| Таким образом максимальная мощность в нагрузку передаётся при равенстве выходного сопротивления активного двухполюсника и сопротивления нагрузки. В этом случае говорят, что сопротивление нагрузки согласовано с выходным сопротивлением источника электрической энергии или с выходным сопротивлением источника сигнала. |
| |
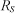 и
и 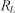 измеряются в омах, выразим для упрощения дальнейших математических выкладок величину
измеряются в омах, выразим для упрощения дальнейших математических выкладок величину 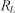 через коэффициент пропорциональности k, показывающий, во сколько раз сопротивление нагрузки
через коэффициент пропорциональности k, показывающий, во сколько раз сопротивление нагрузки 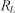 отличается от выходного сопротивления активного двухполюсника
отличается от выходного сопротивления активного двухполюсника 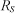 :
: 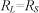 . Максимум мощности в нагрузке при k=1 хорошо виден на графике, приведенном на рис.2:
. Максимум мощности в нагрузке при k=1 хорошо виден на графике, приведенном на рис.2:  2015-02-04
2015-02-04 1329
1329