Вырожденное базисное допустимое решение и вырожденная задача ЛП

Если на каком-либо шаге наибольшее возможное значение переменной (оценочное отношение) достигается в нескольких уравнениях одновременно, то разрешающим можно выбрать любое из этих уравнений. На следующем шаге получится вырожденное базисное решение (одна из базисных переменных равна нулю), а переход к очередному базисному решению может не изменить значения целевой функции.

Пусть в примере 1 запас ресурса R₃ равен 4 единицам. Тогда на первом шаге получим одинаковые оценочные отношения в третьем и четвертом уравнениях.

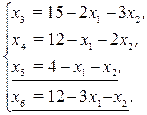
Выражая переменную х₁ из четвертого уравнения и подставляя в остальные уравнения, получим:

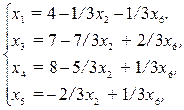
Целевая функция примет вид: 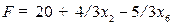. Новое базисное решение (4, 0, 7, 8, 0, 0). Значение целевой функции 20 >0. Произошло увеличение значения целевой функции, но в выражении для F есть переменная х₂ с положительным коэффициентом. Т.е. ее увеличение могло бы привести к росту значения целевой функции. Однако любое её увеличение, отличное от нулевого, приведет к недопустимому значению переменной х₅. Формально переведем переменную х₂ в базисные переменные (вместо х₅). Выразим её из последнего уравнения и подставим в остальные:

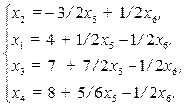
Целевая функция примет вид: 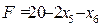. Новое базисное решение (4, 0, 7, 8, 0, 0). При этом значение целевой функции не изменилось и не может быть увеличено, т.к. в выражении целевой функции нет положительных коэффициентов при неосновных переменных.