2015-02-04
1173
Рассмотренный простейший симплекс-метод склонен к зацикливанию и медленно сходится, если длина ребра симплекса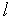 
выбрана малой (выбор же большой длины ребра симплекса обеспечивает высокую скорость сходимости, но дает малую точность решения). Поэтому в вычислительной практике используются различные модификации простейшего метода, направленные на преодоление его указанных недостатков.
Основной идей модифицированного симплекс-метода является изменение по некоторому правилу размера симплекса в процессе поиска. При этом наряду с условием (8) в качестве условия окончания итераций можно использовать условие
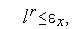| (9) |
где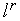 
- текущая длина ребра симплекса, 
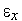- требуемая точность решения по 
.
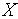Обычно размер симплекса изменяется при выполнении следующих условий:
· при «накрытии» симплексом дна оврага или точки минимума;
· при циклическом движении.
«Накрытие» симплексом дна оврага или точки минимума. Пусть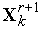 
- вершина, которая получилась на 
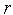-ой итерации в результате отражения вершины 
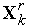. Так что координаты вершин нового симплекса равны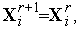 
.
|
|
|
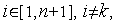
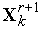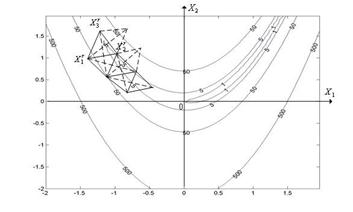
Ситуация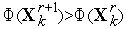 
интерпретируется как «накрытие» этим симплексом дна оврага или точки минимума и простейший симплекс-метод модифицируется следующим образом (см. рис. 5):
1. Полагаем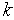 
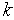= +1 (если = 
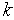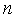+2, то полагаем 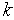=1);
2. Выполняем отражение 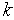-ой вершины симплекса 
;
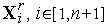3. Если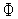 
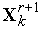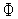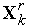()> () и не все вершины перебраны, то переходим к п.1.
4. Иначе - продолжаем итерации по схеме простейшего симплекс-метода 
|
