(1) Если 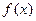 непрерывна при
непрерывна при 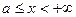 , то несобственным интегралом по бесконечному промежутку называют
, то несобственным интегралом по бесконечному промежутку называют
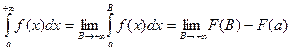
(2) Если 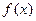 непрерывна при
непрерывна при 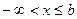 , то
, то
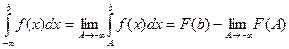
(3) 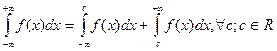
(4) 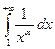 . При
. При 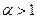 интеграл существует (сходится), при
интеграл существует (сходится), при 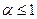 интеграл расходится
интеграл расходится
(5) признак сходимости и расходимости несобственных интегралов 1-го рода (признак сравнения): если 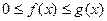 при
при 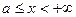 , то из сходимости
, то из сходимости 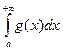 следует сходимость
следует сходимость 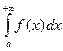 , из расходимости
, из расходимости 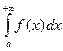 следует расходимость
следует расходимость 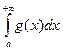
 2015-02-04
2015-02-04 575
575








