Фазовая траектория

В предыдущих подразделах различные колебательные процессы описывались соответствующими дифференциальными уравнениями, решения которых были представлены в виде зависимости смещения x от времени t: x=x(t). Такое описание колебательных систем можно назвать координатным, поскольку, зная явный вид зависимости координаты x от времени t, можно однозначно определить состояние системы в любой момент времени.

Однако состояние любой механической системы, состоящей из n материальных точек можно однозначно описать, задав координаты и импульсы всех материальных точек: x₁, y₁, z₁; x₂, y₂, z₂;...; xn, yn, zn; m₁v₁_x; m₁v₁_y, m₁v₁_z;...; mnvnx; mnvny; mnvnz. Введем в рассмотрение воображаемое 6n-мерное пространство (3 n — пространственных координат и 3 n — импульсных). Такое пространство называют фазовым. Состоянию системы с определенными значениями координат и импульсов всех материальных точек будет соответствовать в этом пространстве фазовая точка с координатами (x₁, y₁, z₁; x₂, y₂, z₂;...; xn, yn, zn; m₁v₁_x; m₁v₁_y, m₁v₁_z;...; mnvnx; mnvny; mnvnz). Эта точка при изменении состояния системы будет перемещаться в фазовом пространстве, описывая некоторую линию, которая называется фазовой траекторией. Для колебательной системы, имеющей одну степень свободы, фазовое пространство вырождается в фазовую плоскость с координатными осями x и .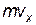

Найдем вид фазовой траектории для затухающих колебаний. В этом случае зависимость смещения x от времени t имеет вид

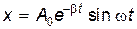где b — коэффициент затухания.

Отсюда

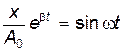(21.75)

Продифференцируем последнее выражение по времени. После деления на w получим

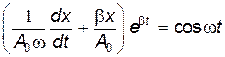(21.76)

Возведем в квадрат обе части уравнений (21.75) и (21.76), сложим полученные выражения и затем умножим на 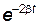. В результате получим уравнение фазовой траектории для затухающих колебаний:

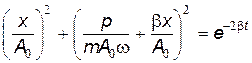(21.77)

где 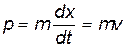— значение импульса.

Вид фазовой траектории показан на рис. 21.30. В процессе затухающих колебаний точка в фазовой плоскости движется по спирали, приближаясь к началу координат.

Фазовую траекторию для гармонического осциллятора можно найти из (21.77), положив b=0. Имеем

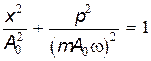(21.78)

т.е. в этом случае фазовая траектория представляет собой эллипс, обегаемый фазовой точкой за время, равное периоду колебаний (рис. 21.31).


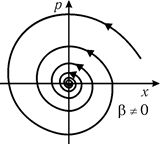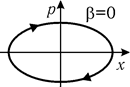Рис. 21.31	Рис. 21.30

Можно показать, что такой вид фазовой траектории для незатухающих колебаний является следствием закона сохранения энергии для гармонического осциллятора. В самом деле, для гармонических колебаний

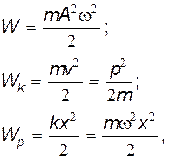
где W, Wk, Wp — соответственно полная, кинетическая и потенциальная энергия. Так как W=Wk+Wp, то 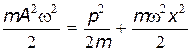, откуда следует уравнение для фазовой траектории (21.78).