Любое сложное колебательное движение может быть представлено как совокупность гармонических колебаний с различными частотами и амплитудами. Совокупность таких колебаний называется спектром. Для того, чтобы найти спектр колебаний, т.е. разложить сложное колебательное движение на отдельные гармонические составляющие, поступают следующим образом.
Пусть сложное колебание описывается периодической (с периодом T), но не гармонической функцией f(t)=f(t+T). По теореме Фурье эту функцию можно представит в виде суммы гармонических составляющих:
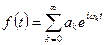 , , | (21.71) |
где 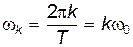 ; гармоническое колебание с амплитудой ak и частотой k называют часто гармоникой. Основная гармоника (k=1) с частотой w1 =w 0 называется тоном, гармоника с частотой Δk = 2w Δ0,... — обертоном.
; гармоническое колебание с амплитудой ak и частотой k называют часто гармоникой. Основная гармоника (k=1) с частотой w1 =w 0 называется тоном, гармоника с частотой Δk = 2w Δ0,... — обертоном.
Для нахождения амплитуд гармоник умножим (21.71) на 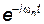 и проинтегрируем в пределах от 0 до T:
и проинтегрируем в пределах от 0 до T:
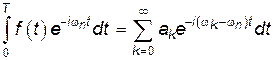 , , | (21.72) |
Интеграл в правой части (21.72) легко вычисляется:
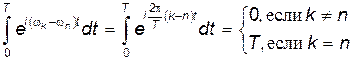 .
.
Таким образом, в сумме, которая фигурирует в правой части (21.72), остается только одно слагаемое с k=n. Поэтому
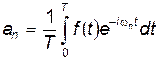 .
.
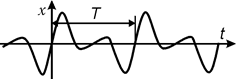 Рис. 21.27 Рис. 21.27 |
На рис. 21.27 как пример показан график сложного колебания, являющегося суммой трех гармоник:
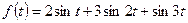 .
.
Из этого графика практически невозможно определить число гармоник, их амплитуды и частоты. Если же построить спектр этого колебания, т.е. зависимость амплитуды от частоты (рис. 21.28), то непосредственно видно, что рассматриваемое колебание состоит их трех гармоник с амплитудами A1=2, A2=3, A3=1 и частотами w1=1, w2=2, w3=3 c-1.
Чем сильнее исходное колебание отличается от гармонического, тем богаче его спектр, т.е. тем больше гармоник содержится в разложении (21.71). В общем случае спектр сложного колебания содержит бесконечный ряд гармоник, амплитуды которых быстро убывают с увеличением их номера, так что практически в разложении (21.71) приходится принимать во внимание только некоторое конечное число обертонов. Экспериментально гармоники могут быть найдены с помощью набора осцилляторов, собственные частоты которых выбраны с определенным шагом (частотомер). Тогда при воздействии сложного импульса на этот набор будут резонировать те из осцилляторов, собственные частоты которых близки к частотам гармоник в разложении (21.71).
 2015-02-04
2015-02-04 3629
3629
