Определение. Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности.
Пусть дискретная случайная величина 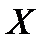 задана рядом распределения
задана рядом распределения
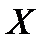
| 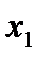
| 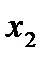
| … | 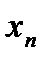
|
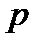
| 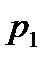
| 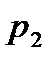
| … | 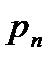
|
тогда математическое ожидание 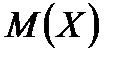 случайной величины
случайной величины 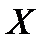 определяется равенством
определяется равенством
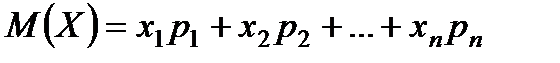 .
.
Если дискретная случайная величина 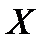 принимает счетное множество возможных значений, то
принимает счетное множество возможных значений, то
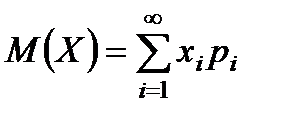 .
.
Пример 2. Найдем математическое ожидание дискретной случайной величины, зная закон ее распределения:
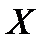
| |||
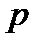
| 0,2 | 0,3 | 0,5 |
Решение. 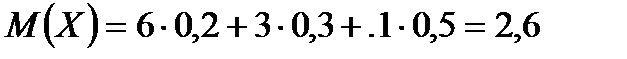 .●
.●
Математическое ожидание приближенно равно среднему арифметическому наблюдаемых значений случайной величины.
Свойства математического ожидания
1.о Математическое ожидание постоянной величины равно самой постоянной:
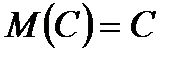 .
.
2.о Постоянный множитель можно выносить за знак математического ожидания:
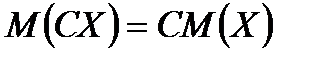 .
.
3.о Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий:
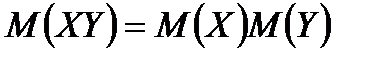 .
.
4.о Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых:
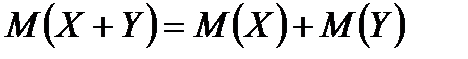 .
.
Пусть производится 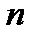 независимых испытаний, в каждом из которых вероятность появления события
независимых испытаний, в каждом из которых вероятность появления события 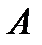 постоянна иравна
постоянна иравна 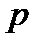 .
.
Теорема. Математическое ожидание числа появлений события 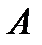 в
в 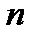 независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании:
независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании: 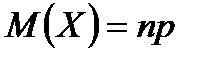 .
.
 2015-02-14
2015-02-14 579
579








