Пусть производится 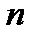 независимых испытаний, в каждом из которых вероятность появления события
независимых испытаний, в каждом из которых вероятность появления события 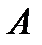 равна
равна 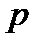 – испытания в схеме Бернулли. Обозначим вероятность ненаступления события
– испытания в схеме Бернулли. Обозначим вероятность ненаступления события 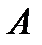 через
через 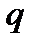 . Очевидно, что
. Очевидно, что 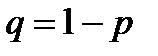 .
.
Найдем вероятность того, что при 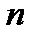 испытаниях событие
испытаниях событие 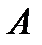 появится
появится 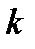 раз. Обозначим эту вероятность
раз. Обозначим эту вероятность 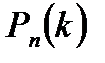 .
.
Вероятность одного события: 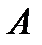 появилось
появилось 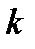 раз и не появилось
раз и не появилось 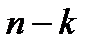 раз равна
раз равна
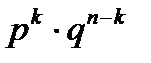 .
.
Число таких событий равно 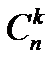 . Так как эти события несовместны, то по теореме сложения вероятностей несовместных событий искомая вероятность равна сумме всех возможных сложных событий. Поскольку вероятности этих событий равны между собой, то их сумма равна вероятности одного события, умноженной на их число.
. Так как эти события несовместны, то по теореме сложения вероятностей несовместных событий искомая вероятность равна сумме всех возможных сложных событий. Поскольку вероятности этих событий равны между собой, то их сумма равна вероятности одного события, умноженной на их число.
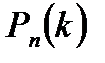
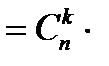
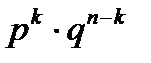 .
.
Полученная формула носит название формулы Бернулли.
Пример 5. В цехе 6 моторов. Для каждого мотора вероятность того, что он включен, равна 0,8. Найти вероятность того, что в данный момент: а) включено 4 мотора, б) включены все моторы, в) выключены все моторы
Решение. Имеем 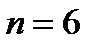 ,
, 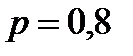 ,
, 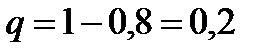 .
.
а) по формуле Бернулли при 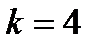 получим
получим
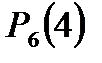
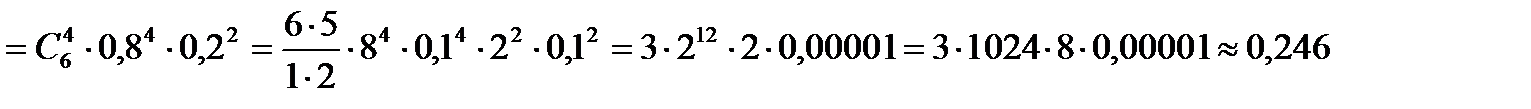 .
.
б) по формуле Бернулли при 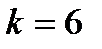 получим
получим
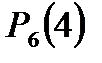
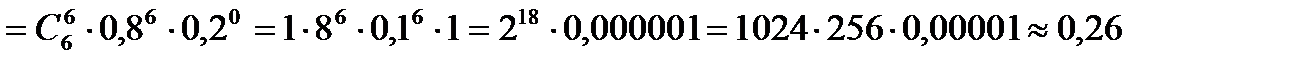 .
.
в) по формуле Бернулли при 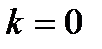 получим
получим
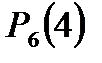
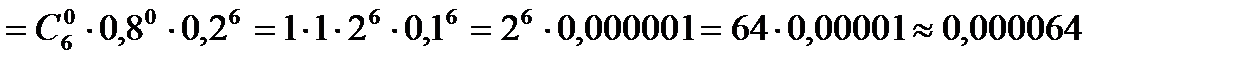 .?
.?
Если число испытаний 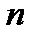 велико, то применяется локальная теорема Лапласа (1783 г.):
велико, то применяется локальная теорема Лапласа (1783 г.):
Если вероятность появления события 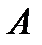 в каждом испытании постоянна и отлична от 0 и 1, то вероятность того, что событие
в каждом испытании постоянна и отлична от 0 и 1, то вероятность того, что событие 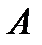 в
в 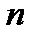 испытаниях появится
испытаниях появится 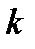 раз, приближенно равна значению функции
раз, приближенно равна значению функции
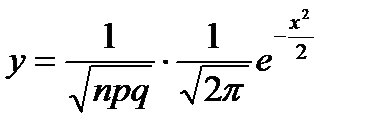 , где
, где 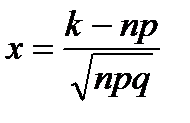 .
.
Функция 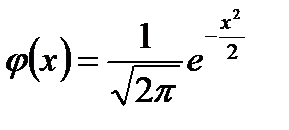 задается таблицами для
задается таблицами для 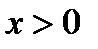 ,
, 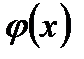 – четная функция, т.е.
– четная функция, т.е. 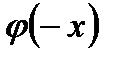
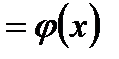 .
.
Таким образом, получаем
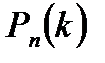
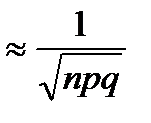
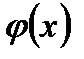 при
при 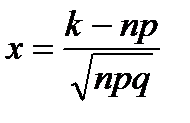 .
.
Пример 5. Найти приближенно вероятность того, что при 400 испытаниях событие наступит ровно 104 раза, если вероятность его появления в каждом испытании равна 0,2.
Решение. По условию, 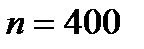 ,
, 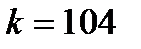 ,
, 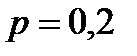 ,
, 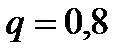 .
.
Воспользуемся формулой Лапласа
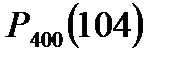
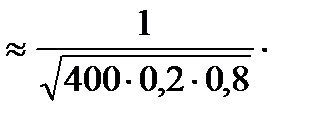
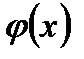
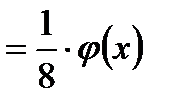 .
.
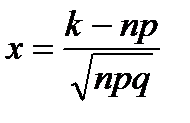
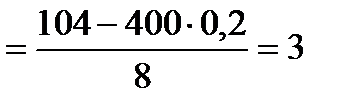 .
.
По таблице находим 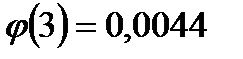 .
.
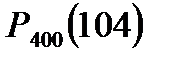
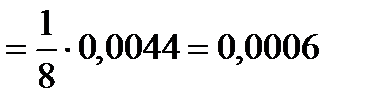 .?
.?
Интегральная теорема Лапласа:
Если вероятность наступления события 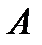 в каждом испытании постоянна и отлична от 0 и 1, то вероятность того, что событие
в каждом испытании постоянна и отлична от 0 и 1, то вероятность того, что событие 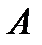 в
в 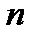 испытаниях появится от
испытаниях появится от 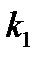 до
до 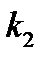 раз приближенно равна
раз приближенно равна
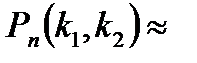
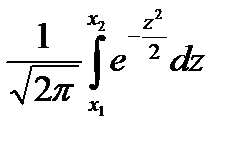 ,
,
где 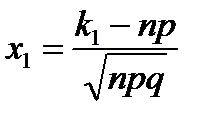 ,
, 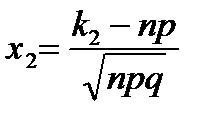
Функция Лапласа 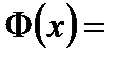
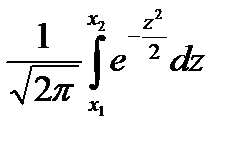 задается таблицами.
задается таблицами.
Свойства функции Лапласа.
1о. 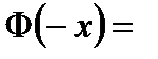
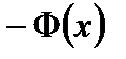 .
.
2о. При 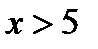
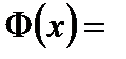 0,5.
0,5.
Таким образом, получаем
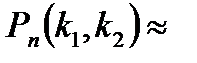
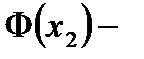
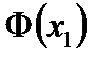 ,
,
где 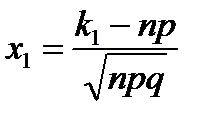 ,
, 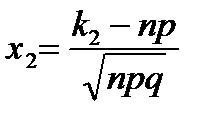
Пример 6. Вероятность поражения мишени стрелком при одном выстреле равна 0,75. Найти вероятность того, что при 100 выстрелах мишень будет поражена а) не менее 70 и не более 80 раз; б) не более 70 раз.
Решение. а) По условию, 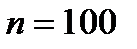 ,
, 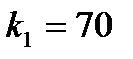 ,
, 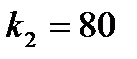
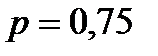 ,
, 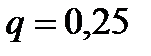 .
.
Воспользуемся интегральной теоремой Лапласа:
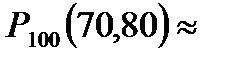
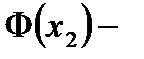
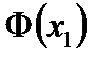 ,
,
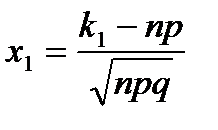
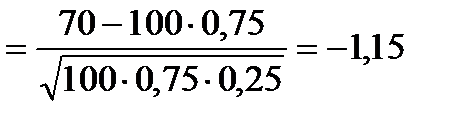 ;
;
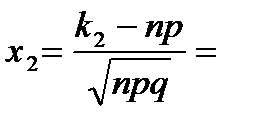
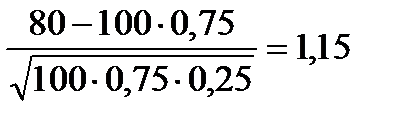 .
.
Таким образом, имеем:
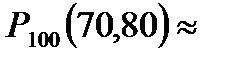
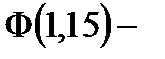
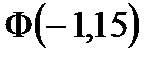
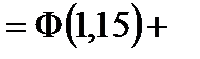
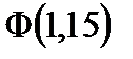
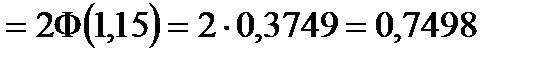 .
.
б) По условию, 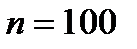 ,
, 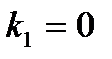 ,
, 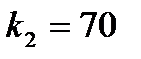
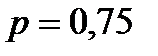 ,
, 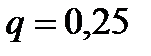 .
.
Воспользуемся интегральной теоремой Лапласа:
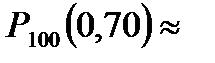
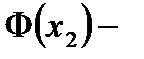
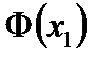 ,
,
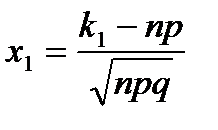
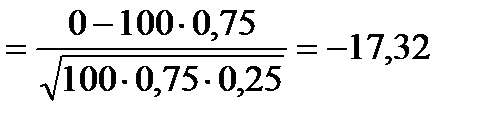 ;
;
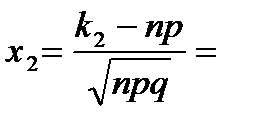
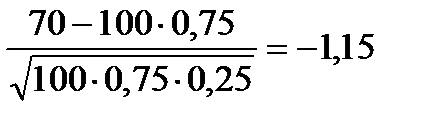 .
.
Таким образом, имеем:
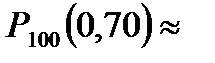
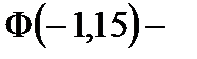
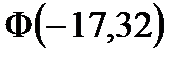
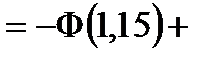
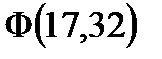
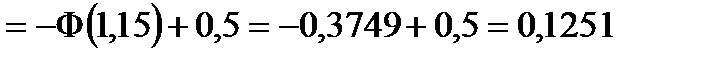
С помощью функции Лапласа можно вычислить вероятность отклонения относительной частоты от постоянной вероятности:
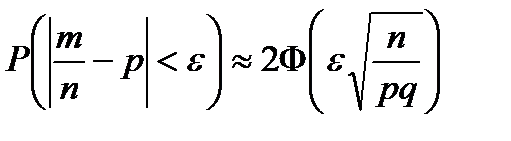 .
.
Пример 7. Вероятность появления события в каждом из 10 000 независимых испытаний равна 0,75. Найти вероятность того, что относительная частота появления события отклонится от его вероятности по абсолютной величине не более чем на 0,001.
Решение. По условию, 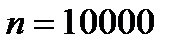 ,
, 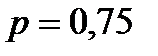 ,
, 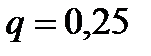 ,
, 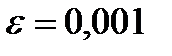 .
.
Требуется найти вероятность 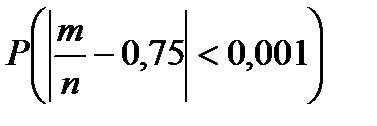 .
.
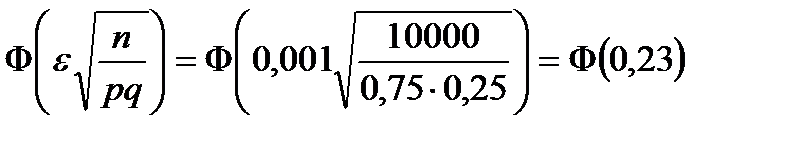
Получим: 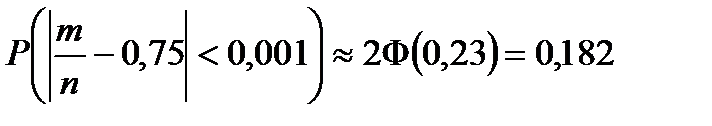
Пример 8. Вероятность появления события в каждом из независимых испытаний равна 0,2. Найти, какое отклонение относительной частоты появления события от его вероятности можно ожидать с вероятностью 0,9128 при 5000 испытаниях.
Решение. По условию, 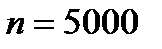 ,
, 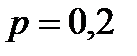 ,
, 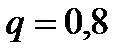 ,
, 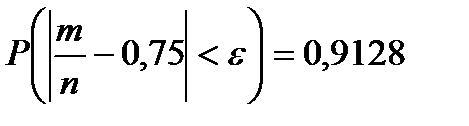 .
.
Так как 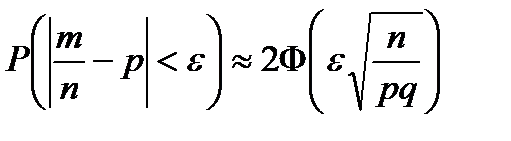 , то имеем
, то имеем 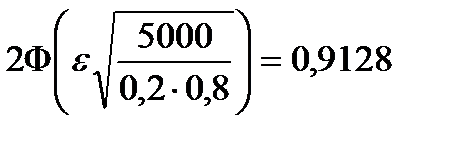 или
или
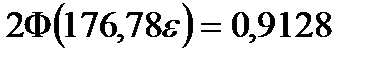 ,
, 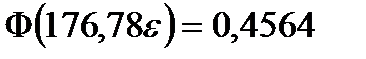 .
.
По таблице находим, что 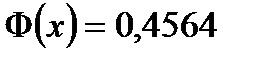 при
при 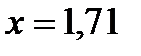 . Значит,
. Значит, 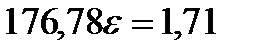 и
и 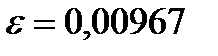 .
.
 2015-02-14
2015-02-14 21091
21091
