Гладкие валки листовых станов

При прокатке листового или полосового материала (фиг. 206, а) шириной В давление металла на валок распределяется по этой ширине равномерно и максимальный изгибающий момент может быть опреде­лен по формуле:

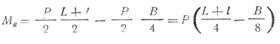(272)

Крутящий момент бочки валка определяется аналогично предыду­щему. Шейка валка рассчитывается на изгиб по формуле:

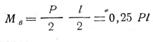(273)

По найденному результирующему моменту и моменту сопротивле­ния определяется действительное напряжение в шейке валка.

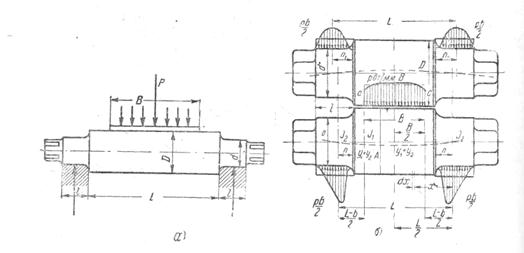
Фиг. 206. Валки листовых станов: а — схема действия сил на гладкий валок листового стана;

б — распределение давлений на валки по Касуэлу

Удельное давление шейки валка на подшипник определяется из ус­ловия, что общее давление на валок распределяется между двумя шей­ками, причем на каждую из них равномерно:

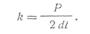(274)

Помимо расчета на прочность, валки тонколистовых станов и ста­нов холодной прокатки проверяются на упругую деформацию, что вы­зывается необходимостью иметь точную прокатку по всей ширине ли­ста при весьма жестких допусках на толщину.

Неравномерность толщины полосы объясняется упругой деформа­цией валков, получающих прогиб при прокатке. Для устранения этой неравномерности валки изготовляют с незначительной выпуклостью посредине бочки. Во время работы валки, прогнувшись на величину выпуклости, выравниваются, и толщина полосы получается одинаковой по всей ее ширине.

То обстоятельство, что полоса получается неравномерной толщи­ны по ее ширине было отмечено целым рядом авторов (Мелоне, Тринкс, Соболевский и др.), но их объяснения этого явления не были исчерпывающими (см. И. М. Павлов и Галлай [121]).

По Гертцу радиальное сжатие абсолютно упругих цилиндров при всех прочих равных условиях возрастает по мере увеличения удель­ного давления. Поэтому в центре валка, где удельное давление боль­ше, чем по краям, радиальное сжатие тоже сильнее. Кроме того, воз­растает сдерживающее влияние частей валка, находящихся вне обжа­тия при деформации.

С увеличением диаметра валков возрастает их радиальное сжа­тие, и, следовательно, неравномерность полосы по толщине увеличи­вается.

Итак, на неравномерность полосы влияют прогиб и радиальное сжатие валков, поэтому при калибровке валков для станов холодной прокатки им придают незначительную выпуклость, могущую компен­сировать прогиб валка во время прокатки металла:

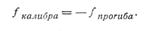
Считая обычную теорию изгиба балок неприменимой для валков, вследствие малого отношения диаметра валка к его длине, Сельвин Касуэлл [122] принимает прогиб валка равным:

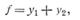(275)

где 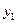— стрела прогиба под действием изгибающих усилий;

— стрела прогиба под действием перерезывающих сил.

Распределение напряжений при обычном изгибе изображается по способу Сельвин Касуэлла [122] параболической кривой (фиг. 206, б).

Обозначим через:

М — изгибающий момент в любом сечении на расстоянии х от точ­ки приложения результирующего давления на шейку валка;

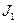и 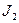— моменты инерции сечений бочки и шейки валка;

р — давление прокатки в тоннах на 1 мм длины бочки валка;

Е — модуль упругости материала валков, т/мм ,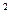

В — ширина прокатываемой полосы, мм;

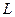— расстояние между точками приложения результирующей давления в шейке валка, мм;

п — расстояние между краем бочки валка и точкой приложения результирующей давления в шейке валка.

Стрела прогиба 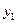под действием изгибающих усилий опреде­ляется интегрированием:

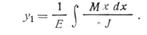
Изгибающий момент реакции опоры:

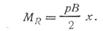
Изгибающий момент от равномерно распределенной нагрузки на элементарной площадке :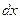

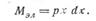
Суммарный момент определяется интегрированием:

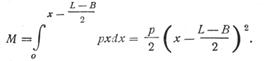(276)

Следовательно:

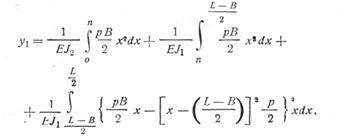
После интегрирования получаем:

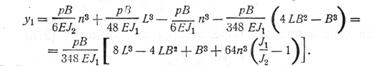(277)

Подставляя вместо отношения моментов инерции бочки и шейки 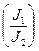отношение их диаметров 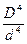,получаем выражение для стрелы прогиба в таком виде:

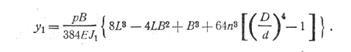(278)

Для верхнего валка Касуэлл принимает 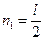для нижнего 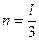, где 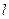— длина шейки валка.

Обозначим:

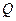— полное перерезывающее усилие в любом сечении, т;

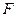—поперечное сечение в любом месте валка, мм ;

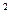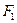и 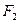— соответственные поперечные сечения бочки и шейки валка, мм ,

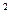С — модуль жесткости материала валков, т/мм 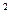. Стрела прогиба под действием перерезывающих усилий, одинако­вая в любом сечении валка,

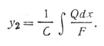
По теореме Шведлера:

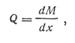(279)

тогда

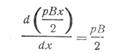
и

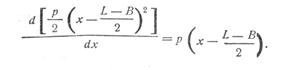
Следовательно:

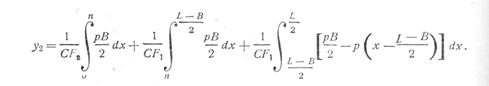
После интегрирования и преобразований получаем в окончатель­ном виде выражение для стрелы прогиба от действия перерезыва­ющих сил:

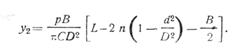(280)

Полная стрела прогиба определяется из равенства (275)

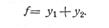
По Иванову максимальная стрела прогиба определяется из урав­нения:

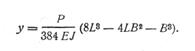(281)

Сравнивая уравнение (281) с уравнением (278), мы убеждаемся, что оно является частью формулы Касуэлла, причем совершенно не учитывает, что диаметр шейки меньше диаметра бочки.

Для упрощения формулы подсчета максимального прогиба валок рассматривают как балку, свободно лежащую на двух опорах.

Если прокатывается полоса, ширина которой значительно меньше длины бочки, максимальный прогиб в центре валка определяется из выражения:

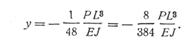(282)

При прокатке полосы, ширина которой близка к длине бочки, мак­симальный прогиб в центре валка:

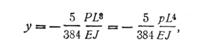(283)

где Р — давление прокатки, кг;

р — удельное давление, кг/мм .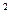

Если полоса занимает определенную часть длины бочки валка, не такую, как в рассмотренных случаях, то в формулы для определения прогиба [282] и [283] необходимо ввести поправочный коэффициент.

Подставляя значения момента инерции валка 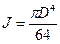в уравнение (281), получаем прогиб:

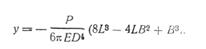
Обозначая 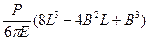через С, получаем:

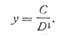
При Р=рВ зависимость прогиба валка от ширины полосы В представляется в таком виде:

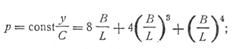
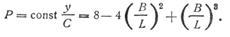
Зависимость прогиба валка от его длины 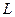при В = 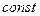(принимая ):

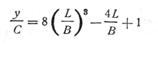
Для практических подсчетов максимального прогиба валка можно пользоваться упрощенной формулой Иванова.

Обозначая 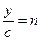, где С = 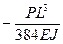получаем для прогиба выражение:

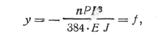(284)

где 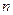— определяется по таблице для данного соотношения 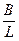(см. ниже).

При В = 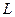, т. е. 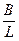=1 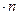= 5, выражение приводится к формуле для случая равномерно распределенной нагрузки.

При В 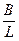= 0; =0; 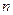= 8, выражение приводится к формуле для случая прогиба балки при сосредоточенной нагрузке.

При практических подсчетах прогиба валка по упрощенным фор­мулам ошибка достигает 5—10%.