Примеры. перед ними отдельные фигуры или пары А- и B-фигур

А -фигур В -фигур

Рис. 9

перед ними отдельные фигуры или пары А- и B -фигур. В этих парах фигур один из членов пары, B -фигура, не имеет осмысленного A -решения, тогда как для A -фигуры возможно A -решение. Некоторым детям кажется, что А- и B -фигуры не отличаются друг от друга. Все они являются новыми. «Откуда нам знать!» — вот их позиция. Они либо никак не реагируют, либо если и реагируют, то не дифференцируют А- и B -фигуры, проводят вспомо­гательные линии и отвечают наугад.

Другие же последовательно решают A -задачи и иногда через короткое время отвергают B -задачи со словами: «Этого я не могу сделать, я не знаю, чему равна пло­щадь», или даже: «Я не знаю, какова площадь этих не­больших остаточных элементов». В отличие от этих слу­чаев в A -случаях площадь остатков, как правило, не упо­минается; или же ребенок говорит: «Я, конечно, не знаю

площади этих маленьких фигур, но, поскольку они рав­ны, это не имеет значения».

Рис. 10

7. В приводимых здесь фигурах A -фигуры, если рассматривать их по частям, сильнее отличаются от перво­начальной фигуры, чем B -фигуры. Поэтому простая ссыл­ка на «знакомость», очевидно, не может служить объясне­нием позитивных реакций — решения в A -случаях и отка­за от решения в B -случаях.

Наши наблюдения в опытах с А — B -парами уже со­держали примеры экспериментального анализа. Хотя за­дача кажется достаточно простой, на классных занятиях иногда встречаешься с глупыми ответами.

8. На следующем этапе экспериментального анализа вместо одной фигуры давались два подвижных твердых тела. Они могли быть отделены или примыкать друг к другу в различных положениях:

А

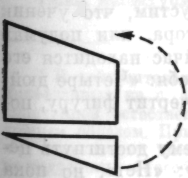
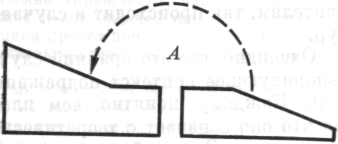
Рис. 11

И в этом случае возможны — и иногда встречаются глупые ответы.

9. Для того чтобы уяснить возникающие здесь теоре­тические вопросы, полезно рассмотреть крайние случаи. Рассмотрим следующую глупую реакцию.

Рис. 12 Рис. 13

Ученика учат доказательству теоремы о площади па­раллелограмма с помощью фигуры, начерченной на мил­лиметровой бумаге. Проводятся дополнительные линии. Сторона а оказывается равной 5 дюймам, длина отрезка с равна 3 дюймам.

Учитель говорит: «Посмотри! Из каждого верхнего уг­ла я опускаю перпендикуляр длиной в 4 дюйма; я про­должаю линию основания вправо на 3 дюйма, ты можешь ее измерить».

Через некоторое время дается другой пример — парал­лелограмм с другими размерами. Допустим, что ученик отвлекся, возможно, на экспериментатора, или подумал о предстоящей игре или о том, где сейчас находится его мама; допустим, что он повторяет про себя: «Четыре дюй­ма вниз, три дюйма вправо» — и робко чертит фигуру, по­казанную на рис. 13.

Когда его спрашивают, удалось ли ему достигнуть це­ли— определить площадь, он отвечает: «Нет», но пока что не может продвинуться дальше. Сам я не сталкивал­ся с таким ответом, но он вполне возможен. Как известно учителям, так происходит в случаях более сложных струк­тур.

Очевидно, что это крайний случай B -реакцпи — слепое, игнорирующее контекст подражание тому, что делал учи­тель. Каждому понятно, чем плохо такое подражание. Но что оно означает с теоретической точки зрения? Мож­но сказать: «Этот ребенок не смог должным образом при-

менить выученный материал к новой ситуации». Но что значит применить «должным образом»?

Или можно сказать: «Ясно, что в этом случае отсут­ствует обобщение» — и покончить с проблемой как с ре­шенной. Но решена ли она действительно? А как быть с глупыми обобщениями, которые остаются тем не менее обобщениями? А что если ребенок обобщит описанный выше пример так (правда, я не встречал таких случаев): «Перпендикуляры должны быть на один дюйм длиннее продолжения основания», или: «Длина перпендикуляра должна выражаться четным числом» и т. д. — и что если он будет соответствующим образом действовать?

Признание того, что здесь имеет место обобщение, не означает решения проблемы. Конечно, здесь имеет мес­то обобщение, но оно происходит в обоих случаях. Часто указание на обобщение не является ответом на вопрос, ско­рее оно скрывает проблему.

10. Что же действительно происходит в А — В- реакци­ях, в А — B -случаях? Я получил характерные данные: встречаются разумные реакции, когда испытуемый отка­зывается слепо применять заученный материал к B -проблемам и находит разумные, правильные решения в A -случаях, меняя обычную процедуру, как того требует здра­вый смысл. И встречаются слепые реакции, когда испытуемые не могут решить А- или B -задачу или тупо применяют заученные приемы ¹.

Если испытуемый применяет заученный прием к ва-

¹ В действительности бессмысленные построения в примерах, приведенных на с. 47, встречаются сравнительно редко. Дети со спонтанной естественной установкой не склонны вести себя по­добным образом. Привычка к бездумному подражанию, развивае­мая в некоторых школах благодаря упору на слепое натаскивание, по-видимому, способствует таким реакциям; то же можно ска­зать о ситуациях, когда такую установку создают рассеянность, отвлекаемость или другие индивидуальные особенности. В школах, ориентируемых на механические упражнения, часто формируется установка при столкновении с новой задачей ждать, что покажут готовое решение; когда ученика просят попробовать решить задачу самостоятельно, часто сталкиваются лишь с пассивным отказом: «Мы этого не проходили».

То, что психолог испытывал какое-то беспокойство на уроке (см. с. 42), означает, что он почувствовал эту атмосферу натаски­вания, царящую в классе. Описанное нами поведение, по-видимому, тесно связано с установкой на повторение, на слепое подражание учителю: обычно маленьких детей не слишком смущает простран-

риации первоначальной задачи, не сознавая, что в данном случае он неуместен, то это свидетельствует о непонима­нии самого приема или о неспособности понять, что яв­ляется существенным в измененной задаче. Но если он адекватно и последовательно ведет себя в A -случаях, даже когда отдельные части измененной задачи сильно отли­чаются от первоначальной, и если он в то же время отка­зывается применять заученный прием к более близким B -вариациям, то это значит, что он действительно понял задачу. Таким образом, А — B -вариации при системати­ческом исследовании могут служить основой «операцио­нального определения» понимания. И с помощью А — В- метода в ходе экспериментального анализа могут быть ис­следованы различные структурные факторы.

В чем состоит основное различие между этими двумя типами реакций на вариации? В чем с психологической точки зрения заключается проблема? Как испытуемый ищет A -решения? Каким образом он различает А- и B -процедуры?

Во-первых, можно сказать: «Различие очевидно. B -реакции в отличие от А -реакций не ведут к правильному решению». Но это утверждение лишь ставит проблему, а не решает ее.

Во-вторых: «Решающее значение имеет степень сход­ства с первоначальной задачей». Нет. Сходство действи­тельно играет роль. Но какое сходство? Если рассматри­вать отдельные части, то окажется, что B -случаи часто ближе к первоначальной задаче, чем A -случаи.

В-третьих: объясняется ли суть дела «обобщением»? Нет. Конечно, во всех этих случаях имеет место обобще­ние, но, как было уже сказано, с глупой B -реакцией мо­жет быть связана такая же степень обобщения, как и с A -реакцией. Таким образом, обобщение само по себе ни­чего не объясняет. Ссылка на обобщение может, конечно, оказаться полезной, если мы будем говорить о «правиль-

ственное расположение фигур (см.: Stern W. Über verlagerte Ra­umformen. — "Zeitschrift für Angewandte Psychologie", 1909, Vol. 2, S. 498-526).

Встречаются и взрослые, которые в дальнейшей жизни сохра­няют приобретенную привычку к слепым, механическим действи­ям. Удивительно, как образованные и в других отношениях вполне разумные люди иногда ведут себя в сходных ситуациях, особенно в случае «Einstellung» (установка), (см. главу 4, раздел 3, а также главу 6 и приложения 2, 3 и 4).

но выбранном обобщении». Но что мы должны понимать под этим уточнением? То, что оно ведет к решению? Это опять напоминает первое утверждение.

В-четвертых, положение дел не изменится, если ска­зать (правильно), что различные A -случаи характеризу­ются тем, что «схватываются» существенные отношения, схватывается то, что действительно релевантно. Но что означает такое «схватывание»? Что такое «существенные элементы»? Как определить, что существенно, а что нет? Только по результату?

Теоретические предположения 2, 3 и 4 не позволяют удовлетворительным образом дифференцировать А- и B -реакции. Только первое предположение дифференцирует случаи, но лишь по результату. Ни одно из этих предпо­ложений само по себе не ведет к психологическому пони­манию.

Я предлагаю читателю подумать над этим. Не удов­летворяйтесь поверхностными решениями. Я думаю, что если вы непредубежденно рассмотрите эти примеры, то найдете ответ. Возможно, он будет вертеться у вас на кончике языка, а вы не сможете выразить его никакими словами. Здесь я прерву свой анализ и вернусь к нему несколько позднее.

II

11. Под влиянием сильного впечатления от странного поведения некоторых школьников психолог снова присту­пает к более тщательному рассмотрению проблемы.

Как и в описанном случае, я часто удивлялся поведе­нию некоторых классов во время урока. Обычно ученики покорно следят за этапами доказательства, которое демон­стрирует им учитель. Они повторяют, заучивают их. Со­здается впечатление, что идет «обучение». Ученики обуча­ются? Да. Мыслят? Возможно. И в самом деле понимают? Нет.

Для прояснения дела была попробована следующая экспериментальная процедура.

Сейчас я скажу нечто странное, даже дикое. Видите ли, по теоретическим основаниям психолог вынужден иногда применять методы, которые для него самого не яв­ляются приятными.

Вместо того чтобы воспользоваться обычным разумным методом определения площади параллелограмма, учени-

кам говорят: «Для определения площади параллелограм­ма следует измерить стороны — назовем их а и £ тить на основании точку, расположенную прямо под верх­ним левым углом; затем измерить расстояние между левой

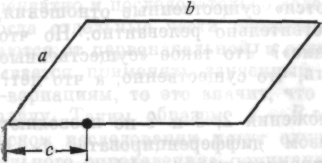Рис. 14

вершиной и этой точ­кой — назовем его с. На нашем чертеже а = 5 дюймов, b = 9 дюймов, с = 3 дюйма. Теперь сложите а и с! (а+с... 5+3 = 8)

Вычтите с из а! (а — с...5-3=2). Перемножьте ре­зультаты! (...8X2=16)

Из произведения извлеките квадратный корень! Вы учили, как это делать (... √ 16=4)

Умножьте результат на b, и вы получите площадь... (... 4X9=36)

___________

Формула площади параллелограмма b√(a+c) (а — с)».

Процедура уродлива и никогда не придет в голову разумному учителю или математику. Это психологу по­требовалось ввести такой громоздкий, некрасивый и бес­смысленный метод. Но он ведет к правильному результату.

Обычно такая процедура кажется детям странной неестественной, — нельзя не заметить, что они время от времени выключаются из работы. По окончании доказа­тельства одни смотрят на учителя с плохо скрываемым презрением. Другие сбиты с толку или смеются.

Важно то, что в некоторых школах нельзя обнаружить существенной разницы между реакцией учеников на та­кое доказательство и реакцией на разумный метод. Если вы обнаружите, что ученики покорно проглатывают такую процедуру и никак не реагируют на нее, обратите внима­ние на характер их обучения! Думаю, что в нем есть что-то порочное. И я надеюсь, что если вы проделаете такого рода опыты, ваши ученики громко рассмеются или по крайней мере будут весьма смущены. В таких случая) особенно трогательно видеть, с каким упорством, с какой готовностью ученики иногда стремятся повторять слова учителя, как гордятся, если им удается точно воспроиз­вести заученное, решить задачу именно тем способом, ко­торому их учили. Для многих в этом и состоит преподава-

ние и обучение. Преподаватель учит «правильной» про­цедуре. Ученики заучивают ее и могут применить ее в рутинных случаях. Вот и все.

Пусть читатель задумается, не учили ли и его самого в школе таким же образом. Разве не таким способом вас обучали дифференциальному и интегральному исчисле­нию? Или даже теоремам планиметрии и стереометрии? Конечно, у вас были веские основания считать, что учи­тель обучает вас разумным, серьезным вещам, которые необходимо знать. Да и что бы вы могли сделать, как не подчиниться и покорно следить за шагами доказательства учителя, если не понимали, почему он предпринимает именно этот, а не иной шаг? Помогало ли вам покорное следование за учителем, когда вы сбивались с пути?

Полагаю, вы согласитесь, что не помогало. Я не удив­люсь, если вы добавите, что, раз учитель действовал таким образом, значит, он, очевидно, действовал правильно, что, вероятно, не было другого пути. Или вы можете возра­зить: «Нельзя сравнивать этот дикий пример с обычным обучением, в ходе которого учитель излагает разумные вещи и их доказательства».

Ваше последнее замечание совершенно справедливо. В нашем примере не хватает доказательства — этого упу­щения, между прочим, некоторые ученики не замечают. Для того чтобы прийти к правильному решению, нам ну­жен пример, включающий доказательство. Мы рассмотрим этот вопрос в пункте 17.

12. Но давайте сначала закончим наш рассказ. Я спро­сил у класса: «Уверены ли вы в том, что этот результат действительно правилен?» Большинство учеников были просто ошеломлены этим вопросом, удивлены, что он мо­жет быть задан. Их позиция была ясна: «Как вы можете подозревать, что мы сомневаемся в ответе, который вы нам дали?» Вопрос показался им странным, он затрагивал самую суть того, что значили для них школа, преподава­ние и обучение. Ответа не было. Класс молчал.

Я изменил свой вопрос и дружески спросил: «Может ли кто-нибудь из вас показать, что полученный таким образом ответ действительно верен?»

Маленький М. поднял руку. Он казался весьма сообра­зительным и ответил: «Я знаю, как это доказать. Это очень просто. Мы установили, что площадь этого парал­лелограмма равна 36 квадратным дюймам. Я могу выре­зать параллелограмм из жести, положить его на одну ча-

шу точных весов, а на другую положить прямоугольник, площадь которого известна и равна 36 квадратным дюй­мам, — держу пари, они уравновесят друг друга».

«Да, они могут уравновесить друг друга, но можете ли вы показать, что так будет всегда?»

«Отчего же, могу, — ответил он. — Я могу повторить эту процедуру с различными параллелограммами».

То, что сказал этот мальчик, характерно для многих случаев мышления. Теперь у него есть слепая процедура плюс способ проверки с помощью взвешивания. И это все; и он вполне удовлетворен. Эта познавательная операция, так называемая индукция, сама по себе превосходная вещь, она часто необходима и в некоторых отношениях играет важную роль в современных эмпирических науках. Вместе с тем в соединении со слепой и, следовательно, дикой процедурой она не является для настоящего мыс­лителя ни действительным решением, ни конечным ре­зультатом. Хотя современная наука часто и основывается на индукции, она не останавливается на ней. Она продол­жает поиски лучшего понимания. (Приведем в качестве примера открытие Менделеева ¹.)

¹ В начале XIX в. английский химик Уильям Праут заметил, что атомные веса химических элементов приблизительно кратны весу атома водорода, и высказал предположение, что водород явля­ется materia prima. На основании этой гипотезы де Шанкуртуа заявил в 1862 г., что свойства химических элементов определя­ются числами. В 1871 г. Менделеев опубликовал свою знаменитую периодическую таблицу классификации химических элементов, в которой все элементы были расположены в восьми вертикальных и семи горизонтальных рядах. Это позволило ему показать, что свойства химических элементов, в частности их валентность, из­меняются в соответствии с изменением их атомного веса. Таким образом, атомный вес Менделеев рассматривал как фундаменталь­ную, важнейшую характеристику элементов. Это подтверждалось тем, что он мог предсказывать открытие неизвестных элементов, которые были необходимы для заполнения пустых мест в его таб­лице, исходя из соображений, основанных на периодичности и на регулярном возрастании атомного веса химических элементов.

Хотя классификация Менделеева была представлена им как чисто эмпирическое обобщение, она ясно указывала на фундамен­тальное единство материи.

В 1913 г., основываясь на атомных теориях Резерфорда и Бора, молодой английский ученый Мозли доказал, что именно числом атомов водорода, образующих атом данного элемента, или, точнее, числом протонов и, следовательно, электронов — атомным номером, а не атомным весом объясняются химические свойства элементов.

Так эмпирическое обобщение превратилось в конечном счете в дедуктивную теорию. — Прим. редактора амер. издания.

Будучи важным инструментом на своем месте, индук­ция сама по себе является скорее началом, а не концом. Но в данном случае она незаконна даже как начало, по­скольку не является необходимой и не связана с сущест­вом дела.

13. Рассмотрим для пояснения другой пример. Учитель демонстрирует классу, как определять площадь паралле­лограмма, проводя дополнительные линии, перенося тре­угольники слева направо и показывая в итоге, что пло­щадь равна произведению основания на высоту. В этом примере я предложил учителю использовать параллело­грамм, одна сторона которого, а, равнялась 2,5 дюйма, а другая, b — 5 дюймам. Была измерена высота h, кото­рая оказалась равной 1,5.

Затем я предложил другие задачи, указывая в каждом случае величину сторон а и b; высота измерялась, и сле­довало определить площадь параллелограмма:

	а	b	Высота (измеренная)	Площадь не­обходимо вычислить
	2,5		1,5	7,5
	2,0		1,2	12,0
	20,0	1⅓	16,0	21⅓
	15,0	1⅞	9,0	16⅞

Ученики решали эти задачи, испытывая некоторые труд­ности с умножением.

Вдруг один мальчик поднял руку. Глядя на тех, кто еще не кончил вычисления, с некоторым превосходством, он выпалил: «Глупо заниматься умножением и измере­нием высоты. Я нашел лучший метод определения пло­щади— он очень прост. Площадь равна а + b».

«Можешь ли ты как-нибудь объяснить, почему пло­щадь равна а + b?» — спросил я.

«Я могу доказать это, — ответил он. — Я вычислил пло­щадь во всех случаях. Зачем ломать голову, умножая b на h? Площадь равна а + b».

Тогда я дал ему пятую задачу: а =2,5; b =5; высо­та = 2. Мальчик начал считать, пришел в смятение, а за­тем, довольный, сказал: «В этой задаче сложение не дает

площади. Прошу прощения; а было бы здорово!»

«В самом деле?» — спросил я.

Это может служить примером слепого открытия, сле­пой индукции. Осмелюсь утверждать, что ни один разум­ный математик не одобрит столь очевидно бессмысленную индукцию. Он прибегнет к ней только в том случае, если исследуемый вопрос настолько темен, что не приходит в голову никакая идея о возможной разумной внутренней связи.

Могу добавить, что настоящая цель этого «нечестного» эксперимента, который, как вы видели, вполне удался, за­ключалась не просто в том, чтобы навести на ложный путь. Посетив этот класс раньше, я заметил, что в поверх­ностном обращении учеников с методом индукции кроется реальная опасность. Я хотел, чтобы эти ученики — и их учитель — ясно почувствовали рискованность такого отно­шения.

Можно, конечно, сказать, что мальчик ошибся в своей гипотезе просто потому, что она не была универсальной, потому, что она была обобщением, основанным лишь на небольшом числе случаев. Но это значит не понять сути дела. Предложенное равенство — площадь = а + b — бес­смысленно, потому что ничего не говорит о внутренней связи между площадью и а+b, о том, почему оно может оказаться разумным хотя бы в одном — единственном случае, поскольку не существует внутренней связи между ними.

14. Приведу еще более простой пример. Вы спрашивае­те ученика:

1) 12=3 умноженное на сколько? Ответ: 4.

2) 56 = 7 умноженное на сколько? Ответ: 8.

3) 45 = 6 умноженное на сколько?

Предположим, что ученик ответил на третий вопрос: «Семь». И когда вы спросили его, почему он так думает, он сказал: «Разве это не очевидно? Четвертая цифра на единицу больше третьей:

1) 12 3 4

2) 56 7 8

3) 45 6 7».

Разве здесь существенно, что ученик основывал свою «гипотезу» на очень малом числе случаев? Нет. Сама ги­потеза нелепа: увеличение чисел в этом случае не имеет никакого отношения к структуре ситуации, к требовани­ям ситуации, к соединению знаком равенства, к смыслу чисел, расположенных слева, к смыслу знака умножения

в правой части. Оно не связано с теми структурными свойствами, которые обусловливают требования к разумно­му решению или осмысленной гипотезе.

15. Теперь мы приведем дополнительные примеры ди­ких процедур, ведущих к правильному ответу. Ошибоч­ным здесь является не отсутствие доказательства, а то, что ни один из шагов этой процедуры не имеет разумной связи с заданием.

Как определить площадь прямоугольника:

I II

1) а – b 2) 1/ a 3) 1/ b 4) вычтите 2) из 3) 5) разделите 1) на результат, полученный в 4)

1) замените a + b на с 2) а 2 3) разделите 2) на 1) 4) вычтите 3) из a 5) умножьте результат на 1)

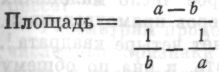
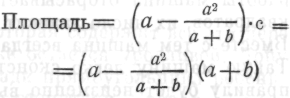
16. Я выбрал искусственные примеры для того, чтобы объяснить суть дела, но подобные вещи случаются и без вмешательства психолога.

Ребенок в школе заучивает вместе с сопутствующими упражнениями формулы для периметра, 2(а + b), и для площади, а ּ b, прямоугольника.

Спустя некоторое время ему предлагаются задачи, тре­бующие вычисления площади прямоугольников в контек­сте решения более широких задач. Ему приходит на ум формула 2 (а+b), и он ошибочно использует ее, даже не подозревая об этом.

Либо он старается вспомнить формулу площади. Он может даже пытаться вспомнить страницу учебника, на которой встречается эта формула, и действительно вспо­минает эту страницу, но формула все же не приходит в голову. Он теряется, смотрит на результат соседа, заме­чает, что найденная площадь равна 25 при сторонах а и b, равных соответственно 10 и 2,5. «Понятно! — говорит он себе. — Теперь я вспомнил, как это делается: 10+2,5= 12,5, умножить это на 2, получается 25; 2(а + b)» — успо­каивается и энергично решает таким способом следующие задачи, получая неверные результаты, но даже не зная об

этом. (Может случиться, что в следующей задаче а =12, b =2,4; так что, взглянув для проверки на результат сосе­да, он убедится в своей правоте.) Ему даже не придет в голову проверить, годится ли вообще в данном случае эта формула. Однако, если бы ученик смело приступил к ре­шению задачи, он, может быть, и сумел бы восстановить самостоятельно даже забытую формулу.

Итак, является ли решающим только то обстоятельст­во, что ученик получил неправильный результат, что его формула не имела общего значения? Для того чтобы за­острить вопрос, представим себе следующую фантастиче­скую ситуацию. Задача вполне может быть решена ма­шиной, которая разрезает прямоугольник на мелкие квад­раты. Вы опускаете прямоугольник в щель, машина начинает работать, маленькие квадраты выпадают из ма­шины и могут быть сосчитаны либо вами, либо суммирую­щим механизмом аппарата. Допустим далее, что в ходе работы машина отбрасывает некоторое число маленьких квадратов, их число зависит от размеров прямоугольника. Вместе с тем машина всегда добавляет четыре квадрата ¹. Такую машину легко сконструировать, и она по общему правилу будет неизменно выдавать результат 2 (а+b).

Исследователь чувствует большое желание заглянуть в машину и выяснить, каким образом почти закономерно получается такой странный результат. Если бы можно было открыть машину и заглянуть внутрь! Но допустим, что это запрещено или даже что такой машины вообще не существует, что все происходит без машины — чудес­ным образом — просто в результате разрезаний и вычис­лений...

Рис. 15

¹ Применение формулы 2 (a + b) для вычисления площади означает, что исчезает площадь т и дважды появляются четыре за­штрихованных квадрата (см. рис 15).

У вас будет универсальный закон, подтверждающаяся неизменно формула, и тем не менее выраженный в этой формуле закон будет диким, слепым, совершенно непости­жимым.

17. Вернемся к нашему вопросу. В наших диких при­мерах отсутствовало доказательство, и могло возникнуть впечатление, что в этом-то и было все дело. В связи с этим рассмотрим, что является условием разумного, осмыслен­ного процесса мышления. Обычно называют следующие условия:

должно быть получено правильное решение,

такое решение достигается благодаря применению ло­гически правильных операций,

правильность результата должна быть доказана, он должен быть правилен во всех случаях.

И это все? Является ли это адекватным отражением того, с чем мы сталкиваемся в реальном, разумном про­цессе?

Рассмотрим процедуру, которая содержит все эти пере­численные признаки и все же остается уродливой. Допу­стим, я рассказываю о площади прямоугольника ребенку, который ничего не слышал о геометрии. Сначала я пока­зываю ему, что площадь квадрата есть а ²: а, умноженное на а. Он усваивает это и вычисляет площади нескольких квадратов различных размеров. Затем я показываю ему прямоугольник и учу находить площадь прямоугольника следующим образом:

Рис. 16

1. Сначала вычти b из а а — b 7—2=5

2. Возведи остаток в квад- (а — b)² 5²=25
рат

3. Возведи b в квадрат и (а—b)²—b² 25—4=21
вычти его из ранее по­-
лученного результата

4. Возведи я в квадрат и (а—b) ² —b ² —а ²21—49=—28
вычти его из результата 3

5. Умножь результат на a ²+ b ²—(а — b)² +28
—1 (сделай его положи­-
тельным)

6. Раздели результат на 2 аb 14

Это — площадь прямоугольника. Это может быть до­казано геометрически, как показано на рисунке:

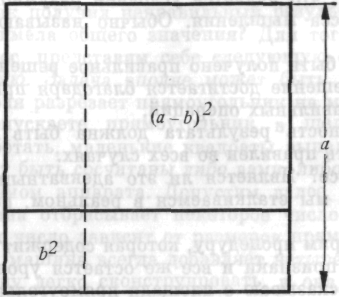
Рис. 17

Доказательство сводится к демонстрации равенства двух прямоугольников и вычитанию общей площади b ². Хотя такое доказательство и является несколько замыс­ловатым, оно с логической необходимостью приводит к решению. Эта процедура не столь уродлива, как преды­дущая, но все же и она уродлива.

Вот некоторые реакции детей: «Что делают взрослые! Почему бы сразу не вычислить площадь? Это похоже на случай с квадратом — число маленьких квадратов в ниж­нем ряду нужно умножить на число рядов».

18. Теперь вернемся назад. Почему описанные про­цедуры «уродливы»? В чем здесь дело?

1) Разве операции выполнены неправильно? Нет, в некоторых примерах операции выполнены совершенно правильно.

2) Разве недостает универсальности? Нет, примеры носили самый общий характер и тем не менее оказались уродливыми (см. пункты 11, 15).

3) Разве недостает наглядности в доказательстве? Нет, некоторые примеры содержат доказательство.

Если мы рассмотрим конкретные действия в этих ди­ких примерах, посмотрим, как ученики подходят к задаче, каким образом отдельные этапы мышления связаны с его» общим направлением, то ответ покажется очевидным: я хочу решить задачу, я столкнулся с проблемной ситуаци­ей; я хочу понять, как можно прояснить задачу, чтобы до­стичь ее решения. Я стараюсь понять, как определяется площадь, как она «встроена» в эту фигуру; я хочу по­нять это. Вместо этого приходит некто и говорит, что я должен делать то-то и то-то, например вычислить 1/ а, или 1/ b, или (а— b), или (а — b)², то есть делать вещи, внут­ренне совершенно не связанные с задачей, ведущие меня в другом направлении, — в направлении, чуждом задаче. Почему я должен делать именно это? Мне говорят: «И все-таки делай», а затем добавляется новый шаг, опять веду­щий в непонятном направлении. Эти шаги совершенно непонятны, их содержание, направление, весь процесс не обусловлены внутренними требованиями ситуации, кажут­ся произвольными, не связанными с вопросом, каким об­разом площадь структурно строится из меньших единиц именно в такой форме. В конце концов эти шаги приводят к правильному или даже доказанному результату. Но сам этот результат воспринимается так, что он не приводит к пониманию и ничего не проясняет. И это относится ко всем примерам и с доказательствами, и без доказательств.

«Послушайте, — скажет возмущенный читатель, — а не требуете ли вы от человеческого мышления слишком мно­гого?» Нет, не требую; к счастью, встречаются не столь слепые процессы.

19. Как показывают реакции детей, позитивный, про­дуктивный ход мышления имеет совершенно иной харак­тер. Вопрос о площади в смысле суммы маленьких еди­ничных квадратов рассматривается в связи с фигурой, в связи с ее характерной формой; ребенок обнаруживает, что существуют параллельные ряды, которые прилегают друг к другу, равны друг другу, содержат одинаковое чис­ло маленьких квадратов. Затем число квадратов в одном таком ряду, определяемое длиной одной из сторон, умно­жается на число рядов, определяемое длиной другой сто­роны. Здесь важно понять, что площадь структурирована в соответствии с характерной формой фигуры. Ни один из предполагаемых шагов не является произвольным, не связанным с внутренней природой проблемной ситуа­ция.

Один и тот же результат (площадь= а - b) психологи­чески имеет различный смысл в разумной и дикой про­цедурах: а-b в осмысленной процедуре рассматривается не просто как «произведение двух членов», поскольку один из них означает число квадратов в одном ряду, а вто­рой — число рядов. Множители имеют различное струк­турное и функциональное значение, и, пока это не будет осознано, формула и даже смысл самого умножения не будут поняты.

Рис. 18

20. Я приведу иллюстрацию последнего утверждения. Мальчику показывают прямоугольник, разделенный на маленькие квадратные части. Ему говорят, что общее чис­ло квадратов — площадь — равно а-b. Теперь, перемножая стороны, он может правильно вычислить площадь несколь­ких предложенных ему прямоугольников. Я спрашиваю его: «Ты уверен, что это правильно?» «Конечно, ведь вы меня научили формуле, но, если хотите, я могу пересчи­тать», — отвечает он. И начинает пересчитывать наборы из пяти квадратов следующим образом:

3	4	5	1	2	3	4	5
5	1	2	3	4	5	1	2
2	3	4	5	1	2	3	4
4	5	1	2	3	4	5	1
1	2	3	4	5	1	2	3

Рис. 19

Закончив подсчет, он поворачивается ко мне: «Вот ви­дите, все верно».

Ясно, что что-то существенное здесь упущено. Мальчик не понял, каким образом из повторения параллельных ря­дов строится площадь. Он не использовал основной струк­турный признак, заключающийся в том, что ряды состоят из одинакового числа квадратов. И таким образом, ему не удалось найти основу осмысленного структурного по­нимания площади.

Другими словами, если бы площадь определялась по­средством вычислений, которые произвел мальчик, то фи­гура совсем не обязательно должна была бы быть прямо­угольником. Подошла бы любая другая фигура, состав­ленная из прилегающих малых квадратов. Действия уче­ника не учитывают внутреннюю связь фигуры с опера­цией умножения.

Подобное структурное понимание (или отсутствие та­кового) играет решающую роль и в переносе. Вот корот­кий пример: в экспериментальных целях ребенку показы­вают, как определяется площадь квадрата. Он овладевает приемом и применяет его в различных случаях, а затем его просят определить площадь прямоугольника. Он не мо­жет ее найти. Я спрашиваю: «Почему бы тебе не посту­пить таким же образом, как ты это делал в случае с квадратом?» Он колеблется, а затем говорит: «Не могу... здесь стороны не равны».

Но если бы на примере квадрата он действительно ра­зобрался в сути дела, понял бы, что площадь следует рас­сматривать как произведение числа квадратов, лежащих в основании, на число рядов, то перенос не вызвал бы ни­каких затруднений. В этом случае равенство сторон квад­рата не было бы помехой, оно структурно было бы пери­ферическим явлением, не имеющим существенной связи с решением.

Перенос может быть и слепым. Без такого понимания можно просто слепо считать, что и площадь прямоуголь­ника определяется произведением двух его сторон. Если называть и этот случай обобщением, то следует ясно по­нимать, что существует важное различие между струк­турно слепыми, или бессмысленными, обобщениями и об­общениями осмысленными.

21. Мне могут возразить: «Почему вы говорите о по­нимании внутренней структуры, внутренних требований, подразумевая при этом, что схватывание структурных при-

знаков в ваших примерах делает действия осмысленными? А что вы скажете о неевклидовых ситуациях? Что если мы выберем для нашей геометрии другие аксиомы? То, что разумно в одной системе, может быть бессмысленным в другой. То, что вы говорите, может показаться разум­ным только тем, кто разделяет наивную старомодную веру в важность только евклидовых аксиом».

Это возражение несостоятельно: оно не затрагивает существа вопроса. Неевклидова геометрия обладает свои­ми собственными структурными признаками, но и в но­вом, более широком контексте сохраняют силу требования осмысленности. После введения признака пространствен­ной кривизны некоторые утверждения евклидовой гео­метрии оказываются непригодными, так как они не учи­тывают условий, появляющихся с введением кривизны, и соответствуют только частному случаю, при котором кривизна равна нулю.

Коротко проиллюстрируем сказанное: фигура, состоя­щая из четырех «прямых» линий и четырех прямых углов на поверхности сферы, отличается от плоского прямоуголь­ника также и площадью, но и в этом случае вы можете либо осмысленно определить эту площадь, поняв ее внут­реннюю структуру, либо получать результаты диким ме­тодом, аналогичным уже рассмотренным нами случаям.

«Почему вы в этом контексте говорите о разумности?— спросит логик. — Разумность — это не что иное, как тре­бование непротиворечивости в смысле старой формальной логики. Любая теорема, любой закон — даже ваш пример площади прямоугольника, равной в описанном вами ис­кусственном мире 2 (а + b),— являются нелепыми или неразумными только потому, что они противоречат другим законам и не согласуются с аксиомами собственной систе­мы. Вот и все».

Но этот аргумент просто переносит вопрос с теорем на аксиомы. Если рассмотреть другие аксиомы, соответствую­щие именно таким структурно слепым связям и обеспе­чивающие формальную непротиворечивость, то в резуль­тате окажутся дикими не только отдельные теоремы, но и вся аксиоматическая система.

Конечно, в современной математике наблюдается тен­денция к построению систем, из которых устраняется структурная осмысленность. Некоторые считают, что сле­дует игнорировать такую осмысленность. Сходная тенден­ция наблюдается и в развитии логики — логика сводится

к игре, управляемой суммой произвольно комбинируемых отдельных правил. Как разделение труда такая специали­зация заслуживает одобрения, особенно когда дело каса­ется критериев строгой логической валидности. Но если к этому сводится все назначение логики, то тем самым мышление лишается тех признаков, которые играют важ­ную роль в действительно продуктивных процессах. Одна­ко, каково бы ни было отношение структурных проблем к формальной логике и теории познания (независимо от ре­шения вопроса о том, следует или не следует логике за­ниматься структурными проблемами), они являются ре­шающим моментом подлинно разумных, продуктивных процессов.

Развитие современной математики происходило в на­правлении полного освобождения от всяких следов гео­метрической интуиции. Это имело свои основания, по­скольку анализировались вопросы валидности идеальных, аксиоматических систем, в которых конкретные теоремы выводятся только путем применения к аксиомам силлоги­стических и сходных формальных операций. Но это впол­не обоснованное стремление не следует смешивать с проб­лемами понимания и подлинно продуктивных процессов. Я не встречал ни одного действительно продуктивного ма­тематика, который не чувствовал бы этого различия. Неко­торые говорили: «Это не логический и не математический вопрос. Это психологический вопрос, или, если угодно, во­прос эстетической стороны дела». Мне кажется, что такие утверждения связаны со слишком узким пониманием ло­гики. К тем шагам и операциям, которые образуют дикие процедуры, приходят не логическим путем. Прямая про­цедура кажется также и более логичной. Различие между произвольными, слепыми и осмысленными действиями со­ставляет самую суть логики.

22. Приведенные примеры и в самом деле были дики­ми и бессмысленными, и читатель вправе спросить, зачем их нужно было приводить. Их искусственность и бессмыс­ленность вполне очевидны; достаточно здравого смысла, чтобы понять их отличие от действительно осмысленных действий. Но в целях научной ясности необходимо сосре­доточить внимание на очевидных вещах. Некоторые тео­ретические построения в логике, теории познания, психо­логин игнорируют эту фундаментальную проблематику или даже пытаются оправдать слепоту к ней.

Более того, то, что мы склонны считать само собой

разумеющимся и «очевидным», нуждается в научном осве­щении и разработке. Здесь я использовал термины, кото­рые кажутся непривычными и недостаточно простыми. Следует, однако, понять, что сама ситуация таит в себе множество проблем. И в этом нет ничего странного. В то время как в традиционной логике существует множество хорошо разработанных операций, операции, с которыми имеем дело мы, все еще плохо изучены. Гештальттеория только пытается их разработать.

23. «Вы не упомянули, — вмешивается логик, — еще одно обстоятельство, достаточное для различения дейст­вий, которые вы называете дикими, и действий разумных. Эти примеры кажутся бессмысленными просто потому, что состоят из большего числа шагов, являются более длин­ными. Вы забыли о „lex parsimoniae"».

Все предыдущие решения действительно содержали большее число шагов, чем соответствующие разумные ре­шения. Но этот внешний признак не должен вводить вас в заблуждение. Он не имеет существенного значения.

Всегда ли такие «мудреные» действия необходимо со­держат большее число шагов? Всегда ли они «сложнее» соответствующих осмысленных действий? Нет. В задачах на определение площади прямоугольника и параллело­грамма осмысленные действия структурно слишком прос­ты, чтобы допустить применение более короткого метода, но в учебниках по математике можно обнаружить такие случаи. Рассмотрим, например, следующую задачу.

Какова сумма ряда:

S=l+ a + a ²+ a ³+ a ⁴...? (a <1)

Вот обычное решение:

1) Напишите равенство 1. S = 1+ а + a ²+ а ³+ а ⁴+...

2) Умножьте обе части 2. aS=a+a ² + a ³ + a ⁴ + a ⁵...
равенства на а

3) Вычтите из первого ра- 3. S — aS= 1

венства второе

4) Найдите S

Вот правильный результат: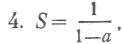

он корректно получен, дока­зан и весьма элегантен из-за своей краткости. Действи­тельное понимание, разумный вывод формулы отнюдь не просты; для этого требуется гораздо большее число нелег­ких шагов. Хотя многие и вынуждены признать коррект-

ность описанных выше действий, они не испытывают чув­ства удовлетворения и чувствуют себя обманутыми. Умно­жение на а, а затем вычитание одного ряда из другого дает решение, но не приводит к пониманию того, как бес­конечный ряд (точнее, последовательность его частичных сумм) приближается в процессе роста к своему предель­ному значению¹. Подлинное понимание исходит из рас­смотрения роста ряда и приводит к закону роста, что по­зволяет найти предел. Многие в действительности не до­стигают понимания. Они удовлетворяются получением правильного ответа².

Существуют математические теоремы, которые в на­стоящее время имеют только «внешние» решения, потому что они остаются все еще слишком сложными для кон­структивного понимания. Крайними примерами их явля­ются некоторые случаи так называемого доказательства от противного, непрямого доказательства, в котором ис­пользуется принцип исключенного третьего, показываю­щий, что принятие противоположной посылки невозмож­но, поскольку оно ведет к противоречию. Но такое до­казательство не позволяет понять, как конструктивно до­стигается позитивное решение. Знаменитый математик Брауэр презрительно называл такие непрямые доказатель­ства «позвоночным мышлением». Я не стану здесь вы­яснять, насколько обоснованно его требование не призна­вать результаты, которые могут быть получены только таким способом. Я лишь хочу подчеркнуть, что сущест­вует огромное различие между осмысленным решением, основанным на понимании сущности задачи, и решением, совершаемым посредством внешних действий.

¹ Вот пример ответа испытуемого в одном из моих экспери­ментов: «Странно... умножение на а... зачем? Разве это приближает меня к цели?.. Вычитание — зачем? А теперь в 3) все, что я знаю о структуре 5, исчезло! Разве я ищу сумму этого возрастающего ряда? Я знаю о ней не больше, чем раньше, — только то, что она равна 1/1- a. Но почему? Как?»

² Конечно, для профессионала и эта обычная процедура явля­ется осмысленной. Она основана на понимании того, что при «сдви­ге», то есть при умножении на а, ряд, за исключением первого чле­на, не изменяется. И все же эта процедура остается внешней и не предполагает действительного понимания того, как возникает сум­ма.

III

24. Прежде чем перейти к рассмотрению подлинных процессов мышления детей в связи с определением пло­щади параллелограмма, мы зададим следующий вопрос: «Каковы этапы действительно разумного процесса опре­деления площади прямоугольника?» Мы коротко перечис­лим этапы, которые считаем существенными, основываясь на экспериментах с детьми и взрослыми.

1) Предлагается задача: чему равна площадь прямо­угольника? Еще не знаю. Как я могу это узнать?

2) Я чувствую, что должна существовать какая-то внутренняя связь между величиной площади и формой пря­моугольника. Какова эта связь? Как я могу ее обнару­жить?

3) Площадь можно рассматривать как сумму малень­ких квадратиков, помещающихся в фигуре¹.

Рис. 20

А форма? Это не любая фигура, не простое нагромож­дение маленьких квадратов; я должен понять, как пло­щадь «строится» в этой фигуре! (Рис. 20.)

4) Разве способ организации, (или возможность орга­низации) малых квадратов в этой фигуре не ведет к яс­ному структурному восприятию целого? Да, конечно. Длина фигуры повсюду одна и та же, и это должно быть связано с постепенным увеличением площади! Параллель­ные ряды малых квадратов прилегают друг к другу и взаимно равны; таким образом они заполняют всю фигу­ру. У меня есть совершенно одинаковые по длине ряды, которые вместе образуют целую фигуру.

¹ Я опускаю здесь процессы, которые начинаются с варьиро­вания размера прямоугольника; введение маленьких квадратов уп­рощает картину. Иногда дети сами находят этот прием; иногда экспериментатор предъявляет прямоугольник, состоящий из куби­ков, или с самого начала проводит линии; в этих случаях детям все еще предстоит самим сделать существенные шаги.

5) Я хочу найти общую сумму; сколько всего в фигуре рядов! Я осознаю, что на это указывает высота — сто­рона а. Чему равна длина одного ряда? Очевидно, она задается длиной основания b.

6) Значит, я должен умножить а на b. (Это не просто умножение двух величин одного и того же рода: на этом этапе существенное значение имеет их характерное функ­циональное различие.)

При таком структурировании прямоугольника ясным становится вопрос о величине площади. Полученная структура прозрачна и легко схватывается. Решение до­стигается ¹ благодаря пониманию внутренней структурной связи между площадью и формой.

25. Я не утверждаю, что именно такие фазы могут быть вычленены в актуальном процессе мышления ². Обычно они тесно взаимосвязаны внутри целостного про­цесса; и все же, по-моему, их выделение необходимо для действительного понимания существа дела.

Эти фазы включают ряд операций и признаков, кото­рые не были по-настоящему оценены или изучены тради­ционной логикой и ассоциативной теорией.

1) Здесь имеет место группировка, реорганизация, структурирование, операции деления целого на части, ко­торые все-таки продолжают рассматривать вместе, в пря­мой связи с целой фигурой и под углом зрения постав­ленной специфической задачи.

Эти операции осуществляются не любым способом, мы имеем дело не с любой группировкой или организаци­ей, хотя фактически существует много различных спосо-

¹ На четвертом этапе вместо горизонтальных рядов можно вы­брать вертикальные. Но в ходе решения не следует смешивать эти два способа. Когда ребенок их путает, легко стирается различие между «числом рядов» и «длиной ряда»; поэтому рекомендуется начинать с прямоугольника, у которого стороны явно различаются. Пятый этап особенно очевиден в случае, когда стороны прямоуголь­ника кратны стороне мерного квадрата; в противном случае про­цедура включает еще один шаг, а именно уменьшение площади мерного квадрата. В 5) и 6) появляется умножение. Но это отнюдь простое или необходимое воспроизведение операции, усвоенной уроках арифметики. Возможно даже, что это нечто совершенно противоположное: сама идея умножения, или смысл умножения, может стать понятной именно в таком контексте.

² Я бы не советовал адаптировать каждый из этих шагов для школьного обучения. Но иногда полезно задать вопрос в одном из указанных направлений.

бов группировки; фазы планируются и осуществляются в соответствии с целостными свойствами фигуры, с целью определить четкую структуру площади.

Решение предполагает понимание того, каким образом части целого складываются друг с другом и заполняют всю площадь, осознание внутренней связи между тем, как они согласуются друг с другом и целостными свой­ствами фигуры, например прямолинейностью ее сторон и т. д.

2) Процесс начинается с желания установить внут­реннюю связь между формой и размером. Это не поиски любого отношения, которое может их связывать, а поиски природы их внутренней взаимозависимости.

Некоторые люди начинают вводить изменения, наблю­дая и изучая, как изменение (например, ширины фигу­ры) влияет на ее форму и площадь, и таким образом улавливают какие-то внутренние отношения.

3) Выделенные отношения этого типа — имеющие смысл с точки зрения внутренней структуры данной си­туации, — которые мы будем называть ρ-отношениями, играют здесь важную роль:

Прилегающие друг к дру­гу равные, прямолиней­ные, параллельные ряды:	образуют прямоугольник, содержащий прямые линии, а не та­кую, например, структу­ру, как ­
Число рядов: Число квадратов в ряду: Умножение:	длина одной стороны длина другой стороны заполнение структуры

4) Здесь наблюдается понимание различного функцио­нального значения частей, то есть двух сомножителей,— важнейший признак продуктивного решения и всякого действительного понимания формулы.

5) Весь процесс является единым последовательным процессом мышления. Это не объединение отдельных опе­раций. Ни один шаг не оказывается произвольным, непо­нятным по своему назначению. Напротив, каждый шаг связан с целостной ситуацией. Ни один из шагов не по­хож на а—b, 1/ а или (а—b) ²из наших бессмысленных примеров.

Основные признаки упомянутых операций коренным образом отличаются от операций традиционной логики и ассоциативной теории, которые слепы к целостности и к структурным требованиям ситуации, порождающим тако­го рода операции.

Надеюсь, что читатель почувствовал удивительную по­следовательность и замечательную ясность такого процес­са, а также его разительное отличие от процессов, состоя­щих из изолированных бессмысленных операций.

26. В отличие от этого описание процесса в терминах одной только традиционной логики или ассоциативной теории выглядит поистине жалким.

Здесь я хочу сделать одно замечание в отношении этих подходов. В традиционной логике важнейшее значение придается универсальности: в понятиях, в суждениях мы хотим обнаружить свойства, общие для многих объектов (в данном случае — общие свойства многих прямоуголь­ников). Аналогично в ассоциативной теории основным яв­ляется вопрос о том, во многих ли случаях, при многих ли повторениях обнаруживается та или иная устойчивая связь. В соответствии с этим бессмысленность наших при­меров индукции объясняется тем, что они не обладают общей валидностыо. Однако вопросы осмысленного струк­турирования, организации, согласования частей друг с другом, соединения их в целое и т. д. не обязательно свя­заны с мыслью о других случаях; они могут осуществ­ляться в отдельном конкретном случае, если рассматривать его структурно, осмысленно. Это, конечно, не обеспечивает фактическую универсальность, но часто приво­дит к осмысленному пониманию и подлинному открытию существенных признаков, в отличие от действий, осно­ванных на слепом обобщении общих признаков, присущих большинству или всем случаям. И это также предполага­ет возможность структурно осмысленного переноса (см. пункт 4), ведущего к пониманию общности и универсаль­ности. Но те или иные фазы решения не обязательны при рассмотрении многих случаев и констатации их общих черт.

27. Обнаружив, что обычных понятий недостаточно, некоторые теоретики пришли к заключению, что мышле­ние становится продуктивным в результате использова­ния принципа отношений. Конечно, понимание отноше­ний играет важную роль в мышлении, но это утверждение само по себе не служит объяснением главного вопроса,

не является его решением. Ибо трудности, с которыми мы столкнулись при анализе элементов, снова возникают и в связи с отношениями. Понимание любых отношений, даже если они установлены правильно, не является ре­шающим; важно, чтобы эти отношения были структурно необходимы, чтобы они возникали, рассматривались и ис­пользовались как части с точки зрения их функции в структуре целого. И это в равной степени относится ко всем операциям традиционной логики и ассоциативной теории, таким, как обобщение, абстрагирование и т. д., ес­ли они применяются в реальных процессах мышления.

Между прочим, бессмысленные и безуспешные про­цедуры предполагают не меньше отношений, чем продук­тивные.

28. Согласно другому современному подходу, можно рассуждать так: «Подчеркиваемое вами различие между бессмысленными и хорошими примерами является в дей­ствительности элементарным и означает только то, что в случаях, которые вы называете бессмысленными, мы ис­пользуем такие средства, шаги и операции, о которых за­ранее неизвестно, что они увенчаются успехом. Тогда как в случае действий, которые вы называете разумными, мне это известно по прошлому опыту. Я, например, заранее знаю, что если некоторое количество разделено на одина­ковые части, то я могу воспользоваться известным мне приемом умножения. Здесь я использую средства, кото­рые связаны с результатами предшествующих упражне­ний. Ассоциация вызывает воспоминание».

Против первой части этой формулировки нечего воз­разить: действительно, в бессмысленных примерах ис­пользуются средства, относительно которых заранее неиз­вестно, помогут ли они. Но вторая часть формулировки является несостоятельной: во-первых, она игнорирует опе­рации согласования, группировки и т. д. и их характер­ные особенности; во-вторых, знание, что между целью и средством существует какая-то постоянная связь, и ис­пользование его еще не решают дела. «Знание» — дву­смысленное понятие. Знание слепой связи, например свя­зи между выключателем и светом, сильно отличается от понимания или открытия внутренней связи между сред­ством и целью, от понимания их структурного соответст­вия в данном случае (см. пункт 38). Это различие играет важную роль особенно в отношении возникновения осмыс­ленного, продуктивного процесса.

Иутверждение, что мы вспоминаем об умножении, ко­торое было усвоено в результате упражнений, не подхо­дит к нашим разумным случаям. Ибо операция умноже­ния и его смысл нередко постигаются благодаря осозна­нию структурных требований именно в таких заданиях. И даже если техника умножения была усвоена раньше н теперь осуществляется по памяти, важно, что именно бы­ло известно и что вспоминается: какие-то слепо приме­няемые заученные операции или же те операции, которые структурно необходимы и вспоминаются и применяются именно по этой причине, а не в результате какой-нибудь случайной ассоциации (например, накануне вы выполни­ли много упражнений на умножение или слышали слово «площадь» в связи со словом «умножение»).

29. Умножение — это не просто операция, которая дол­жна быть заучена и которая характеризуется в терминах ассоциаций, связей между числами. Если оно является осмысленным, то основывается на структурном открытии или понимании, которые необходимы даже при его при­менении. Правда, к сожалению, многих детей обучают умножению с помощью упражнений, и они мгновенно вы­полняют умножение, но не имеют ни малейшего пред­ставления о том, где его следует применять ¹.

¹ Я обыкновенно спрашивал девочку (в доме часто бывали го­сти): «Сколько мужчин и сколько женщин сидит за столом?» «Сколько всего гостей за столом?» Я часто задавал этот вопрос; сначала когда девочке было шесть, затем — семь, потом — восемь лет. В школе она хорошо успевала по арифметике. Когда вы про­сили ее перемножить, скажем, 6 и 2, она мгновенно правильно от­вечала. Но в данном случае, даже если четверо мужчин сидели по одну сторону стола, а четыре женщины — по другую или если мужчины и женщины сидели парами, она начинала нудно пересчи­тывать гостей: «Один, два, три, четверо мужчин; одна, две, три, четыре женщины». И только в возрасте восьми с половиной лет ей пришло в голову, пересчитав мужчин, сказать: «А женщин столько же», или: «Одна, две, три, четыре пары». А она была умным ре­бенком. Она только не понимала связи группировки с количест­вом, так как привыкла считать предметы по одному.

Однако в возрасте шести лет, в более сложной, но структурно более прозрачной ситуации, она поразила меня своими действия-пи. Как и многих других детей, я попросил ее мысленно сосчитать сторон и углов у кубика сахара, а затем — у пирамиды и двойной пирамиды. Она смогла найти ответ структурным методом и применить его к пирамиде и двойной пирамиде, даже к пирамиде с 3х7сторонами, хотя не умела считать до 21 и даже не могла произнести это число.

30. Теперь я расскажу, что происходило, когда я да­вал задачу на определение площади параллелограмма ис­пытуемым — главным образом детям, — после того как вкратце объяснял им, как определяется площадь прямо­угольника, не говоря ничего больше, ни в чем не помо­гая, просто ожидая, что они скажут или сделают. Среди испытуемых были взрослые люди различных профессий, студенты, по реакции которых можно было судить о том, что они совершенно забыли эту теорему, и дети, которые вообще никогда не слышали о геометрии, даже пятилет­ние дети.

Наблюдались реакции различных типов.

Первый тип. Вообще никакой реакции.

Или кто-нибудь говорил: «Фу! Математика!» — и от­казывался решать задачу со словами: «Не люблю матема­тику».

Некоторые испытуемые просто вежливо ждали или спрашивали: «Что же дальше?»

Другие говорили: «Не знаю; этому меня не учили». Или: «Я проходил это в школе, но совершенно забыл», и все. Некоторые выражали недовольство: «Почему вы считаете, что я смогу это сделать?» И я отвечал им: «А почему бы не попробовать?»

Второй тип. Другие энергично рылись в памяти, пы­таясь вспомнить что-нибудь такое, что могло бы им по­мочь. Они слепо искали какие-нибудь обрывки знаний, ко­торые могли бы применить.

Некоторые спрашивали: «Можно спросить у моего старшего брата? Он наверняка знает». Или: «Можно по­смотреть ответ в учебнике геометрии?» Очевидно, это то­же является одним из способов решения задач.

Третий тип. Некоторые начинали пространно рассуж­дать. Они вели разговор вокруг задачи, рассказывая об аналогичных ситуациях. Или же классифицировали ее ка­ким-то образом, применяли общие понятия, относили за­дачу к какой-то категории или осуществляли бесцельные пробы.

Четвертый тип. Однако в ряде случаев можно было наблюдать реальный процесс мышления — судя по черте­жам, замечаниям, мыслям вслух.

1) «Вот эта фигура; как я могу определить величину площади? Площадь фигуры именно этой формы?»

2) «Что-то нужно сделать. Я должен что-то изменить, изменить таким образом, чтобы это помогло мне ясно уви-

деть площадь. Что-то здесь не так». На этом этапе неко­торые из детей чертили фигуру, показанную на рис. 21.

Рис. 21

В таких случаях я говорил: «Хорошо было бы сравнить величину площади параллелограмма с площадью прямо­угольника». Ребенок беспомощно прекращал, а затем во­зобновлял попытки.

В других случаях ребенок говорил: «Я должен изба­виться от затруднения. Эту фигуру нельзя разделить на маленькие квадраты».

Рис. 22

3) Здесь один ребенок неожиданно сказал: «Можете дать мне складной метр?» Я принес ему такой метр. Ре­бенок сделал из него параллелограмм, а затем превратил его в прямоугольник.

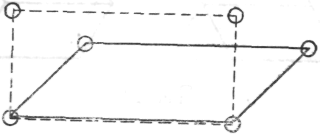
Рис. 23

Мне это понравилось. «Ты уверен, что это правиль­но?» — спросил я. «Уверен», — ответил он. Только с боль­шим трудом с помощью соответствующего чертежа

(рис.24) мне удалось заставить его усомниться в пра­вильности его метода.

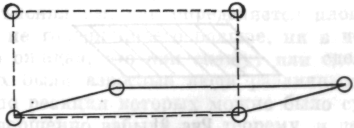
Рис. 24

Тут он сразу сказал: «Площадь прямоугольника го­раздо больше — этот метод не годится...»

4) Ребенок взял лист бумаги и вырезал из него два равных параллелограмма. Затем со счастливым видом со­единил их следующим образом.

Рис. 25

Но он не знал, что предпринять дальше.

Сам по себе этот шаг был прекрасной находкой (ср. решение с кольцом, с. 78). Замечу, что в ряде случаев я сам давал детям два образца фигуры. Иногда я сталкивался с такими реакциями:

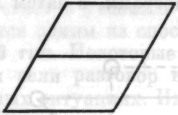
Рис. 26

Некоторые дети даже пытались наложить одну фигу­ру на другую. Такая помощь могла быть эффективной только при некоторых условиях. При каких же именно?

31. Но были случаи, когда мышление вело прямо к цели. Некоторые дети с незначительной помощью или во­обще без всякой помощи находили правильное, разумное, прямое решение задачи. Иногда после периода крайней

сосредоточенности в критический момент их лица свет­лели. Какое чудо — этот переход от слепоты к прозрению, к пониманию сути дела!

Сначала я расскажу о том, что произошло с девочкой пяти с половиной лет, которой я в