Теория Грасгофа и Кодрона

По теории Грасгофа и Кодрона, дополнительно развитой Верещагиным, эле­ментарные давления по дуге захвата не являются постоянными, а изменяются от максимума (при входе металла в валки) до нуля (при выходе из валков) в зависи­мости от произвольного угла :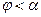

,

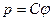где С – коэффициент, показывающий функциональную зависимость удельного давления от величины

угла .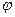

По Грасгофу [62] уменьшение вертикального давления (одним из слагающих которого является радиальное) пропорционально уменьшению толщины полосы или, что то же, величины угла .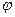

По Кодрону [50] величины элементарных давлений в различных точках проекции дуги АВ на поверхность валка (фиг. 62, а) пропорциональны расстояниям от точки В.

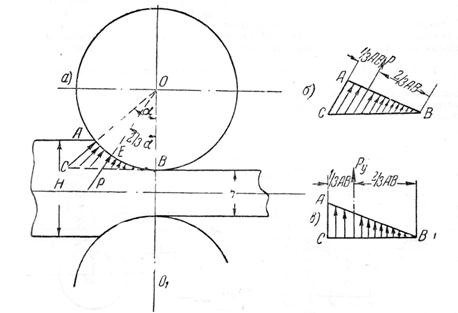
Фиг. 62. Распределение удельных давлений и направление равнодействующей по Кодрону (а и б) и Грасгофу (в).

По Верещагину [63] элементарные (радиальные) давления металла на валок при пластическом состоянии металла пропорциональны первой степени скорости.

Несмотря на некоторые кажущиеся различия в доказательствах, все три автора в разное время пришли к одинаковому выводу, что точка приложения равнодействующей удельного давления лежит по дуге захвата на расстоянии, соответствующем 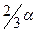от линии центров валков .

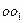Из упомянутых выше все же наибольшей популярностью пользуется вывод Кодрона (фиг. 62, а), по которому, кроме пропорциональности удельных давлений р удалению точек их приложения по дуге захвата от линии центров валков 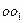(большие катеты), имеет также место пропорциональный рост гипотенузы и малых катетов треугольников АВС, выражающих по Кодрону рост элементарных давлений [61].

Общность всех выводов, предусматривающих изменение удельных давлений, как функции величины угла 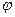, дает основания Кодрону, исходя из пропорциональности общего давления Р большим катетам треугольника АВС, установить зависимость элементарных давлений также от скоростной функции 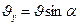, или приближенно 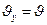, характерной для выводов Грасгофа и Верещагина ( 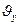- скорость деформации, 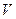- окружная скорость валков).

В заключении следует отметить, что в выводе Грасгофа идет речь не о радиальных элементарных давлениях и их равнодействующей (фиг. 62, б), а о вертикальных силах, слагающими которых является радиальные давления (фиг. 62, в).