Задание на лабораторную работу. Решить уравнения математической модели тепловых процессов ЭМ в среде matlab

Решить уравнения математической модели тепловых процессов ЭМ в среде MATLAB.

Построить графики тепловых нагрузок активных частей якоря с различным типом хладагента и изменениями условий окружающей среды с помощью среды MATLAB.

Выполнить анализ построенных графиков.

Оформить отчет.

Вид хладагента и условие эксплуатации для каждого варианта представлены в Приложении К (таблица К.1).

При работе СГ выделяется теплота, представляющая собой потери энергии, которые возникают при взаимном превращении механической и электрической энергии.

Тепловые потоки, образуясь внутри частей конструкции электрической машины, частично увеличивают их температуру (в неустановившихся режимах), частично путем теплопроводности в телах и теплообмена на их границах поступают в охлаждающие среды (хладагенты) и выносятся из машины.

Основные источники потерь в СГ (обмотки), оказываются отдаленными от хладагента слоями изоляционных материалов, материалами других элементов и т.п. Все эти промежуточные элементы создают тепловые сопротивления тепловому потоку от мест тепловыделения к поверхностям теплообмена с охлаждающей средой (хладагентом). Кроме того, и в самих тепловыделяющих элементах, тепло выделяется почти во всем объеме, поэтому активные элементы также создают тепловые сопротивления от внутренних частей к поверхностям.

При составлении тепловой схемы замещения, которая строится исходя из конструкции генератора типа ГТ, предполагается следующая картина течения теплоты (рисунок 9.1). На рисунке приняты следующие обозначения: 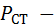потери в стали зубцов и цилиндрической части пакета; 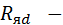ТС по стали ярма в направлении шихтовки; 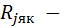ТС стыка ярма с корпусом генератора; 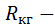ТС корпуса генератора (КГ); 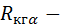ТС перехода от КГ к окружающей среде; 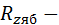ТС по зубцам ярма, от зубцов ярма к хладагенту; 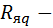от середины пакета (в противоположные стороны); 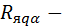перехода от боков сторон ярма к хладагенту (ХА); 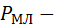потери в лобовых частях обмотки якоря; 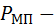потери в меди пазовых частей обмотки якоря; 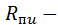ТС пазовой изоляции; 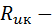ТС клина; 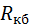– ТС переход клин – хладагент к охлаждающей среде и теплота "течет" в противоположные стороны; 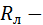ТС меди в аксиальном направлении; 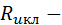ТС изоляции лобовой части меди якоря; 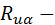ТС перехода от изоляции к хладагенту; 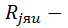ТС изоляции провода в ярме; 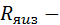ТС стыка ярмо - изоляция паза.

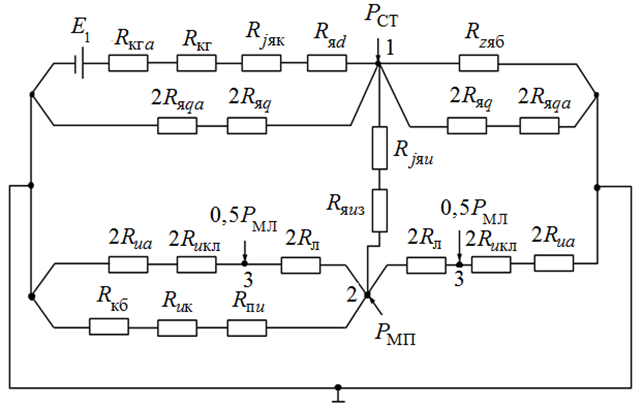
Рисунок 9.1 – Схема распределения тепловых потоков в якоре генератора

Для упрощения схемы якоря, обозначим соединения тепловых сопротивлений следующим образом:

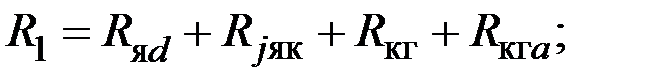
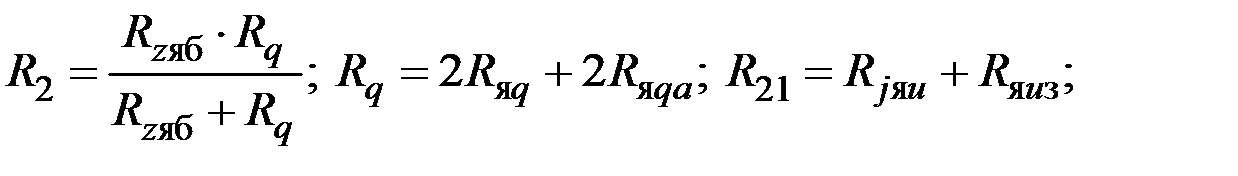
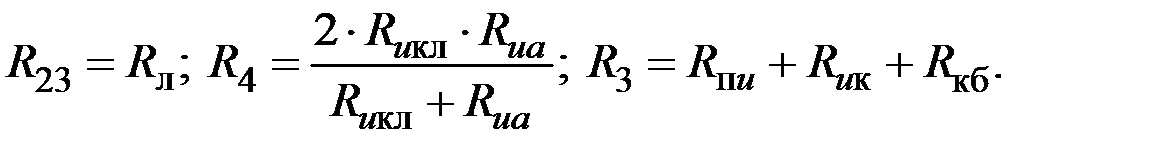
Тогда исходную схему (см. рисунок 9.1) можно представить в упрощенном виде (рисунок 9.2).

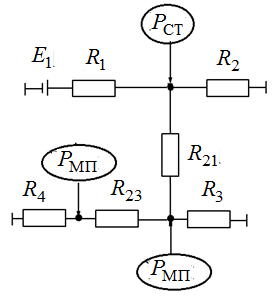
Рисунок 9.2 – Упрощения схема распределения тепловых потоков в статоре генератора типа ГТ

Исходные данные для расчетов (таблица 9.1) и анализа теплового режима приведены применительно к генератору типа ГТ30НЖЧ12 мощностью 30 кВ∙А с жидкостной струйной системой охлаждения.

Таблица 9.1 – Исходные геометрические размеры, коэффициенты, значения тепловых сопротивлений и проводимостей генератора

Формулы вычисления тепловых сопротивлений (ТС)	R, °C/Вт	G, Вт/°C	Исходные данные и размерность: h, l, d- м; S – м2; l - Вт/°С×м; a - Вт/°С×м2.
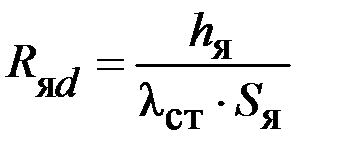
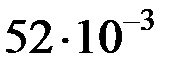
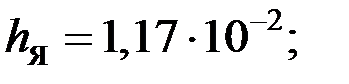
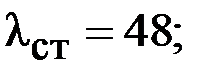
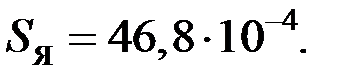
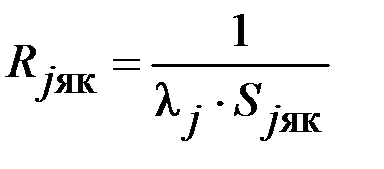
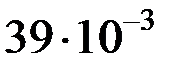
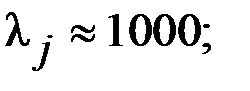
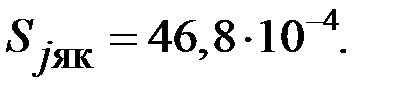
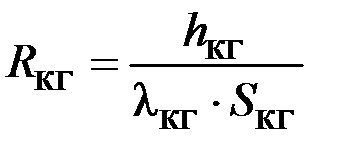
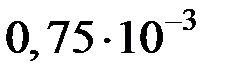
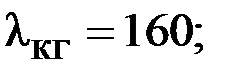
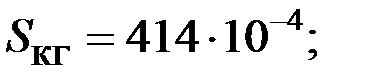
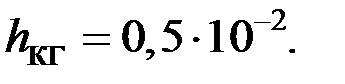
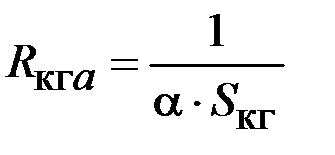
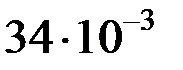
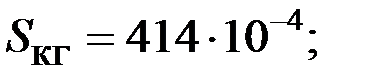
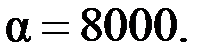
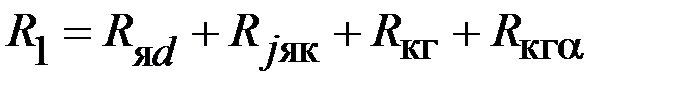
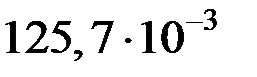
		8,0
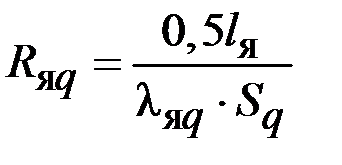
	0,44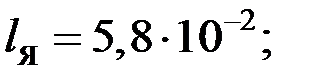
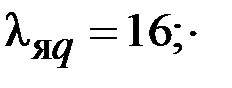
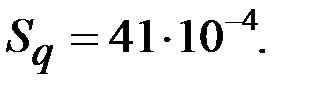
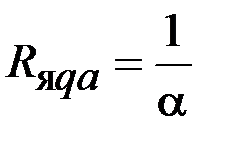
	0,03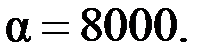
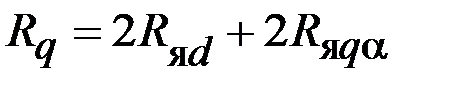
	0,94
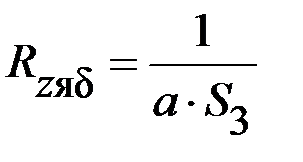
	0,01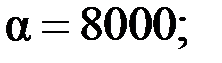
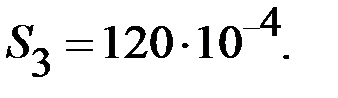
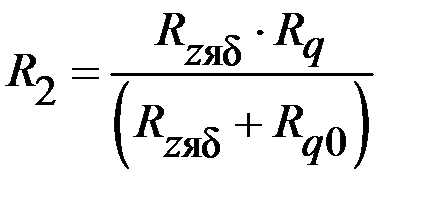
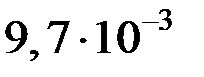
		100,0

Окончание таблицы 9.1

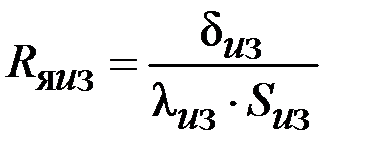
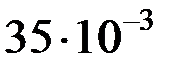
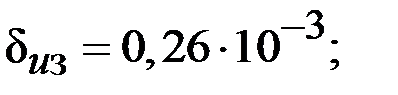
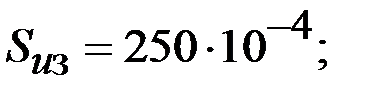
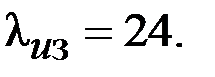
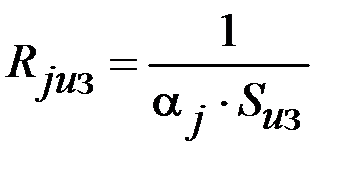
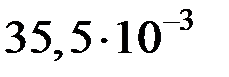
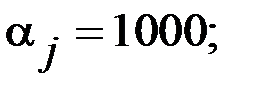
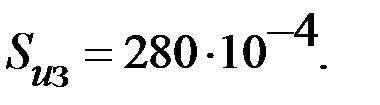
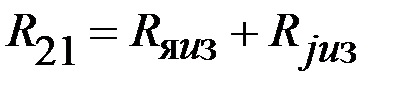
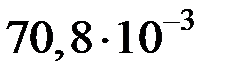
		14,2
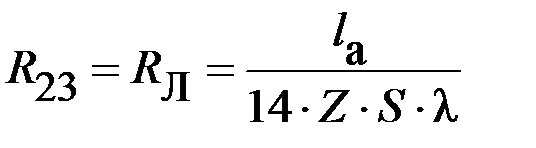
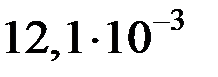
		82,0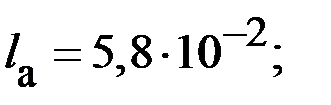
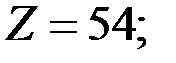
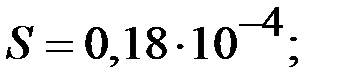
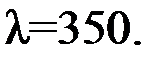
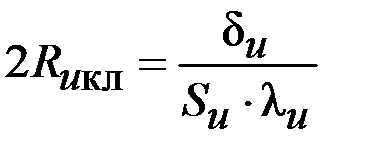
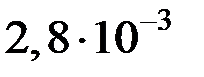
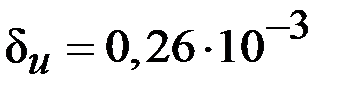
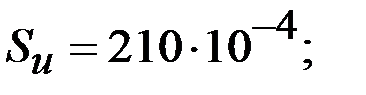
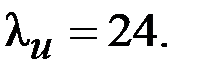
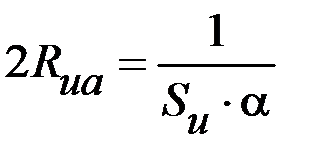
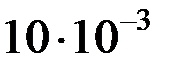
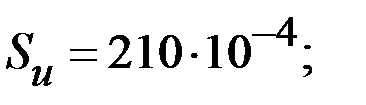
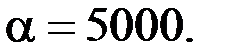
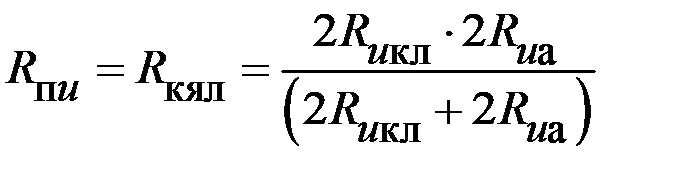
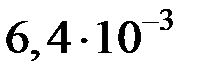
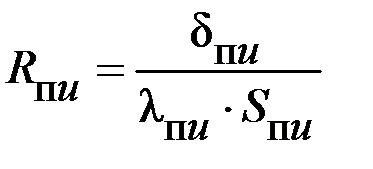
	0,27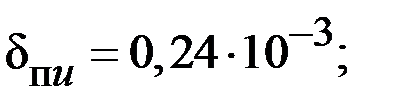
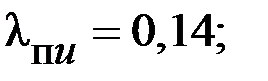
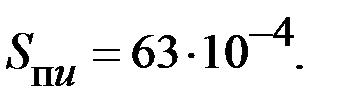
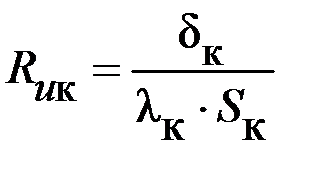
	0,43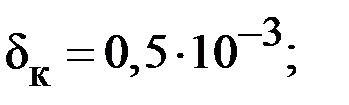
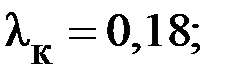
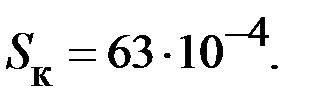
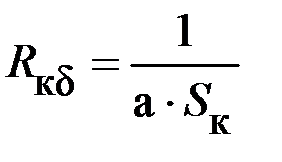
	0,015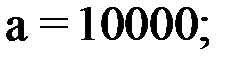
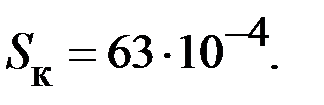
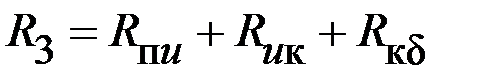
	0,72	1,4

При разработке математической модели тепловых процессов с помощью тепловых схем замещения применяется электротепловая аналогия сопоставляемых электрических и тепловых величин (таблица 9.2).

Таблица 9.2 – Электротепловая аналогия сопоставляемых величин тепловых схем замещения

Электрическая схема	Тепловая схема
Наименование эл. величины	Условное обозначение	Размер-ность	Наименование эл. величины	Наимено-вание эл. величины	Размер-ность
Ток	I	A	Тепловой поток	P	Вт
Падение напряжения	U	B	Превышение температуры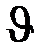
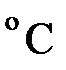
ЭДС источник	E	B	Температура хладагента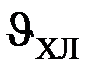
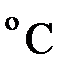
Электрическое сопротивление	R	Oм	Тепловое сопротивление	R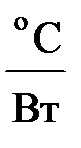
Электрическая проводимость	G	См	Тепловая проводимость	G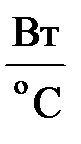
Электрическая емкость	C	Ф	Теплоемкость	cm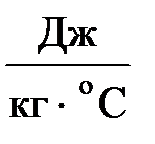

Теперь необходимо тепловую схему замещения представить в виде замкнутой электрической цепи с источниками токов, которые эквивалентны источникам тепла. После составляется эквивалентная тепловая схема замещения статора ГТ (рисунок 9.3), причем тепловые проводимости соответствующих ветвей обозначены через 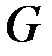, источники потерь представлены в виде идеальных источников тока а температуры хладагента у теплостоков − в виде идеальных источников ЭДС 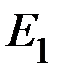, , 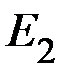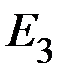и .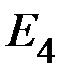

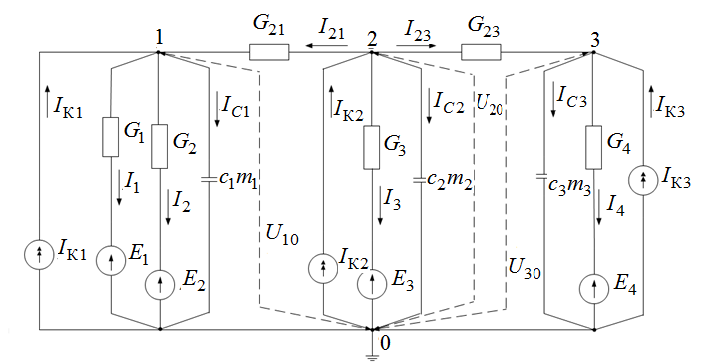
Рисунок 9.3 – Эквивалентная тепловая схема замещения якоря

В соответствии с разработанными выше эквивалентными тепло­выми схемами замещения генератора, используя электротепловую аналогию и метод узловых напряжений, получим уравнения тепловых процессов.

Для якоря (рисунок 9.3) на основании первого закона Кирхгофа запишем:

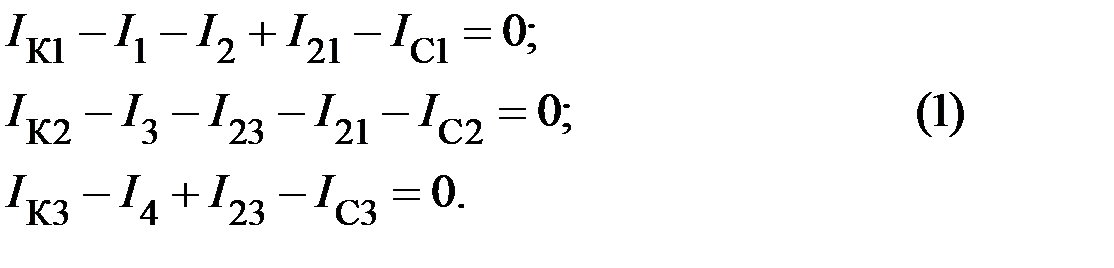
Введем величины узловых напряжений 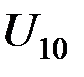, , 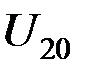, 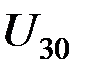соответствующие абсолютным температурам , , 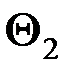, 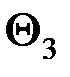активных частей статора (стали, меди в пазу и лобовых частей соответственно):

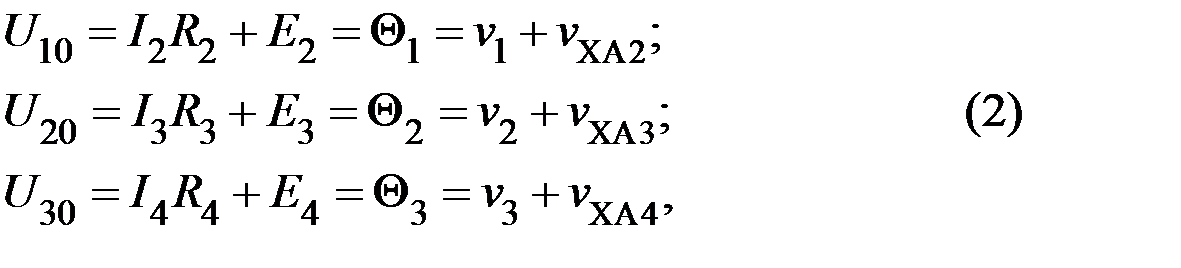
где 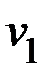, , 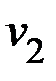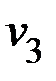– соответственно превышения температуры стали, меди в пазу и лобовой над температурами хладагента 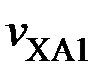, , 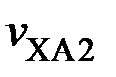и .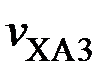

Выразим токи 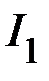, , 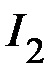, , 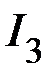, 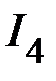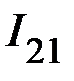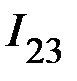через соответствующие узловые напряжения с учетом (2):

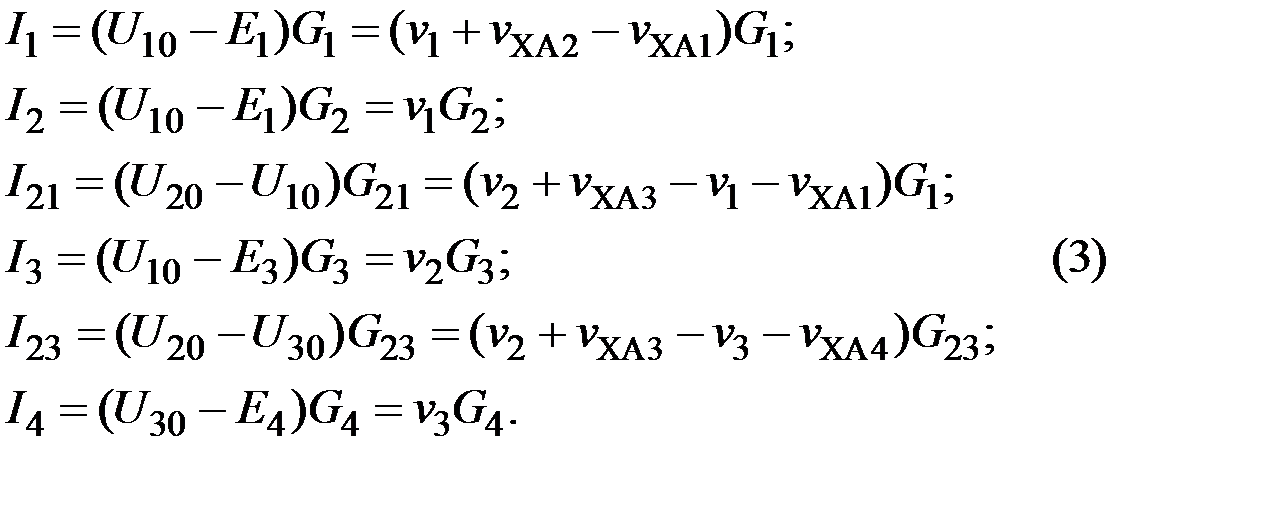
Подставив выражения токов в (1), с учетом 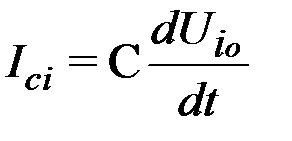и электротепловой аналогии, получим следующие соотношения:

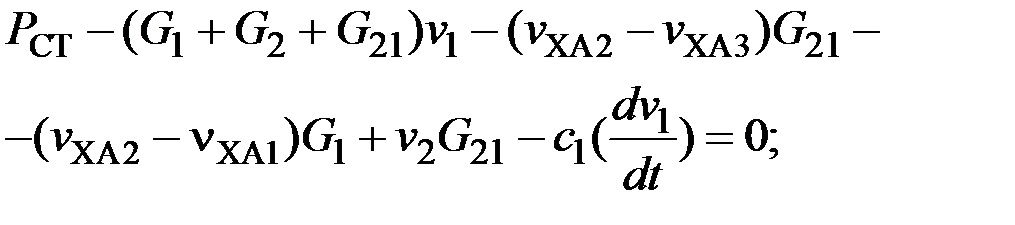
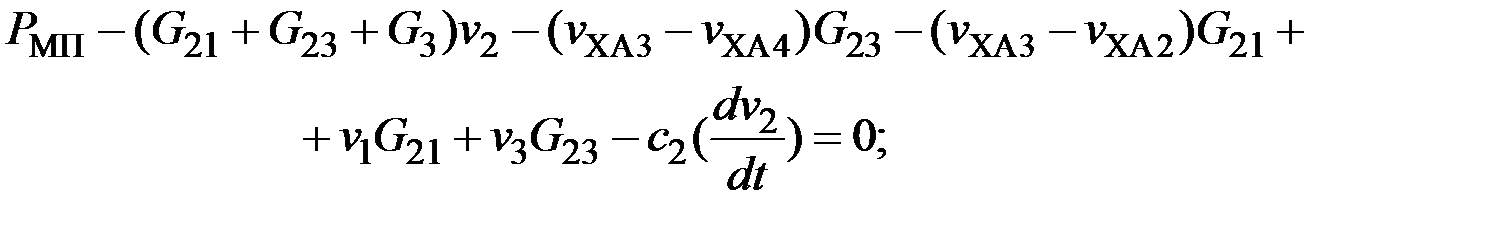(4)

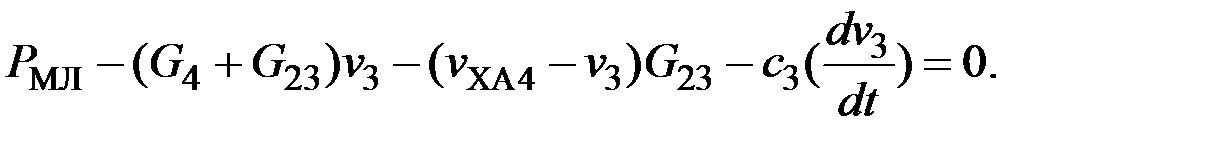
Так как потери в меди в значительной мере зависят от температуры, то:

где 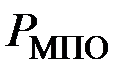, 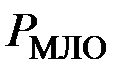– потери в меди паза и лобовых частях при 20°С; 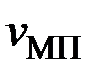, 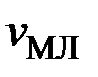– превышение температур пазовой и лобовой меди над температурой 20°С; 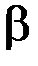– температурный коэффициент меди;

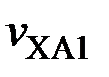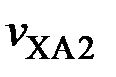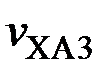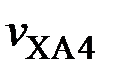, , , – температуры хладагента у соответствующих теплостоков , , , .

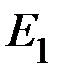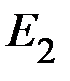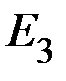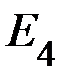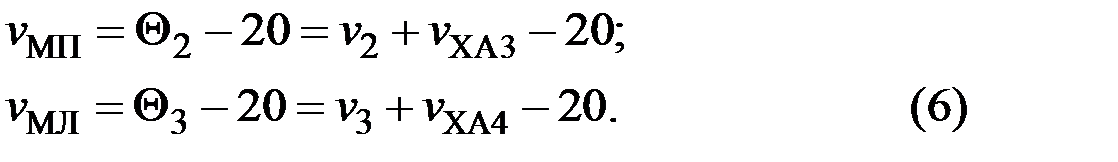
Тогда получим выражения 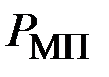и 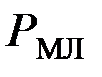в окончательном виде:

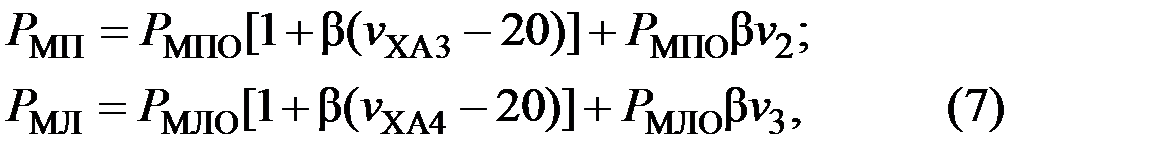
С учетом (7) систему (4) уравнений тепловых процессов статора нужно представить в нормальной форме Коши, которая удобна и необходима для решения этой системы с помощью ЭВМ.

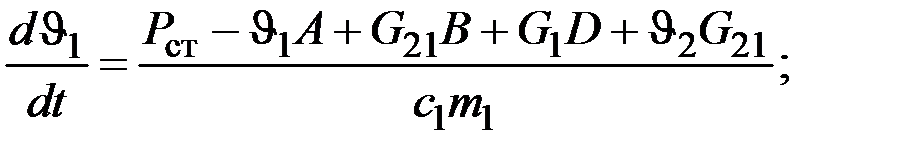
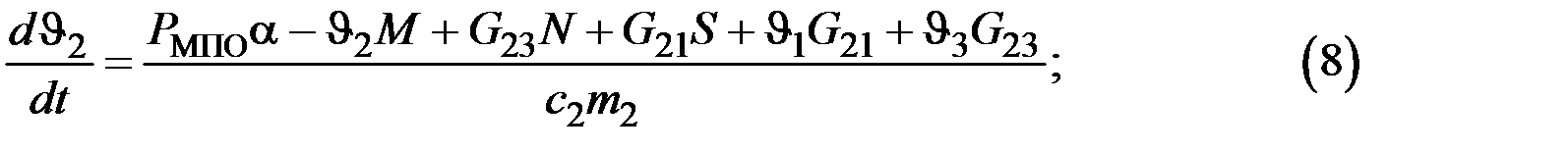
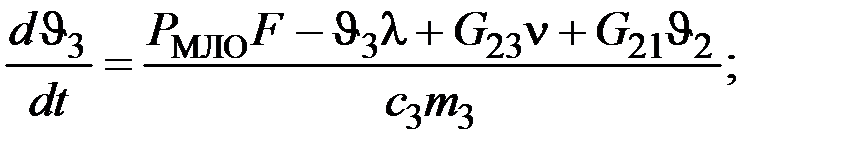
где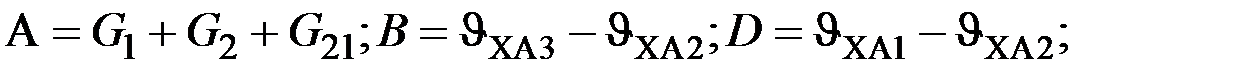

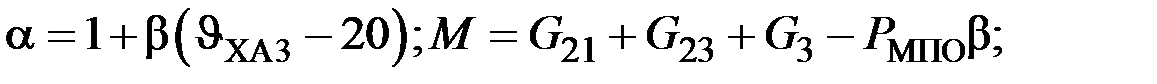
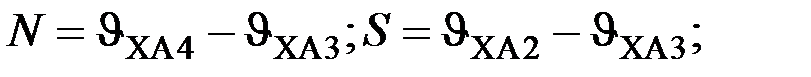
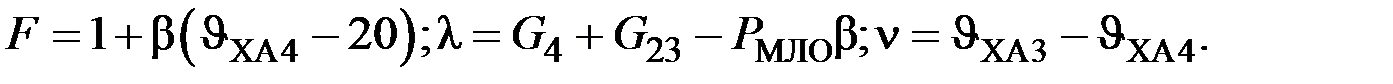
Выведенные формулы далее будут использованы для разработки программы исследования тепловых процессов в среде MATLAB и математического моделирования тепловых процессов в генераторе.