Информатика
Часть 3
Основы вычислительной математики
Методические указания и контрольные работы
для студентов заочного обучения
Составители: С.П. Бобков,
В.А. Бобкова
Иваново 2003
Составители: С.П. Бобков, В.А. Бобкова
УДК 613.19
Информатика. Часть 3. Основы вычислительной математики: Методические указания и контрольные работы для студентов заочного обучения / Сост.: С. П. Бобков, В. А. Бобкова; Иван. гос. хим.-технол. ун-т. – Иваново, 2003. 32 с.
Методические указания являются третьей частью серии методических указаний по курсу «Информатика» для студентов заочного обучения. Рассмотрены следующие темы: приближенное решение нелинейных уравнений; решение систем линейных алгебраических уравнений; решение обыкновенных дифференциальных уравнений; аппроксимация функций с помощью метода наименьших квадратов; линейное программирование. Приведены примеры и задания для выполнения лабораторных работ.
Предназначены для самостоятельной работы студентов заочной формы обучения всех специальностей.
Табл. 9. Ил. 17. Библиогр.: 7 назв.
Рецензент доктор технических наук, профессор А. Н. Лабутин (Ивановский государственный химико-технологический университет)
Введение
Основными целями лабораторного практикума по курсу "Информатика. Основы вычислительной математики" являются:
- закрепление знаний по теоретическим основам использования методов вычислительной математики для анализа математических моделей технических и экономических объектов;
- получение практических навыков работы на компьютерах, отладки и тестирования программ.
Методические указания являются третьей частью серии методических указаний по курсу «Информатика» для студентов заочного обучения. Они содержат описание ряда численных методов, примеры решения конкретных задач и индивидуальные задания для самостоятельных лабораторных работ. В указаниях рассмотрены следующие темы: приближенное решение нелинейных уравнений; решение систем линейных алгебраических уравнений; решение обыкновенных дифференциальных уравнений; аппроксимация функций с помощью метода наименьших квадратов; линейное программирование.
Для реализации численных методов в процессе решения поставленных задач предполагается использование среды программирования Turbo Pascal или процессора электронных таблиц MS Excel.
Требования к оформлению лабораторных работ
Лабораторные работы оформляются в тетради в виде отчета, который должен содержать:
1. Номер варианта
2. Название лабораторной работы.
3. Задание.
4. Расчетная часть:
a. Краткое теоретическое описание метода.
b. Ручной расчет для двух-трёх шагов.
c. Текст программы или описание хода решения задачи с использованием MS Excel.
d. Введенные исходные данные и результаты расчетов.
5. Вывод.
1. Приближенное решение нелинейных уравнений
Пусть дано уравнение с одним неизвестным
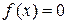 , (1.1)
, (1.1)
где 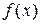 - заданная алгебраическая или трансцендентная
- заданная алгебраическая или трансцендентная 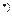 функция.
функция.
Решить уравнение - значит найти все его корни, то есть те значения 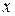 , которые обращают уравнение в тождество, или доказать, что корней нет.
, которые обращают уравнение в тождество, или доказать, что корней нет.
В общем случае не существует формул, по которым определяются точные значения корней уравнения (1.1). Для отыскания корней используют приближенные методы, при этом корни находятся с некоторой заданной точностью 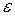 . Это означает, что если
. Это означает, что если 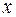 - точное значение корня уравнения, а
- точное значение корня уравнения, а 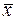 - его приближенное значение с точностью
- его приближенное значение с точностью 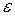 , то
, то 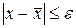 . Если корень найден с точностью
. Если корень найден с точностью 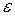 , то принято писать
, то принято писать 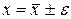 .
.
Будем предполагать, что уравнение (1.1) имеет лишь изолированные корни, то есть для каждого корня существует окрестность, не содержащая других корней этого уравнения.
Приближенное решение уравнения состоит из двух этапов:
1. Отделение корней, то есть нахождение интервалов из области определения функции 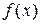 , в каждом из которых содержится только один корень уравнения (1).
, в каждом из которых содержится только один корень уравнения (1).
2. Уточнение корней до заданной точности.
Отделение корней можно проводить графически и аналитически.
Для того, чтобы графически отделить корни уравнения (1.1), строят график функции 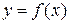 . Абсциссы точек его пересечения с осью Ox есть действительные корни уравнения (рис. 1). Практически бывает удобнее заменить уравнение (1.1) равносильным ему уравнением
. Абсциссы точек его пересечения с осью Ox есть действительные корни уравнения (рис. 1). Практически бывает удобнее заменить уравнение (1.1) равносильным ему уравнением
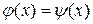 , (1.2)
, (1.2)
где 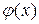 и
и 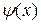 - более простые функции, чем
- более простые функции, чем 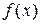 . Абсциссы точек пересечения графиков функций
. Абсциссы точек пересечения графиков функций 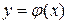 и
и 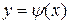 дают корни уравнения (1.2), а значит и исходного уравнения (1.1) (рис.2).
дают корни уравнения (1.2), а значит и исходного уравнения (1.1) (рис.2).
Аналитическое отделение корней основано на следующей теореме: если непрерывная на отрезке 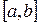 функция
функция 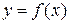 принимает на концах отрезка значения разных знаков, т.е.
принимает на концах отрезка значения разных знаков, т.е. 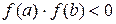 , то внутри этого отрезка находится хотя бы один корень уравнения
, то внутри этого отрезка находится хотя бы один корень уравнения 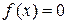 ; если при этом производная
; если при этом производная 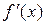 со-
со-

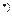 Функция называется алгебраической, если для получения её значения нужно выполнить арифметические операции и возведение в степень с рациональным показателем. Примеры трансцендентных функций - показательная, логарифмическая, тригонометрические, обратные тригонометрические.
Функция называется алгебраической, если для получения её значения нужно выполнить арифметические операции и возведение в степень с рациональным показателем. Примеры трансцендентных функций - показательная, логарифмическая, тригонометрические, обратные тригонометрические.
храняет знак внутри отрезка 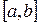 , то корень является единственным.
, то корень является единственным.
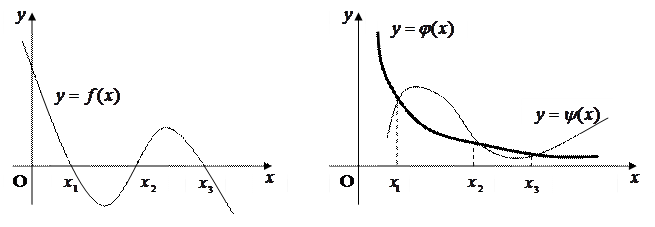
Рис. 1. Рис. 2.
Уточнение корней заключается в сужении интервала изоляции корня и выполняется одним из специальных методов. Рассмотрим самый простой из них - метод половинного деления.
|
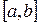 . Находим середину отрезка
. Находим середину отрезка 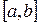 по формуле
по формуле 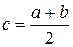 (рис.3). Если
(рис.3). Если 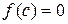 , то с - искомый ко-
, то с - искомый ко-
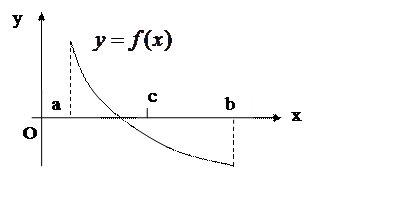
Рис. 3.
вычисляем 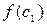 , выбираем отрезок
, выбираем отрезок 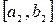 и т.д. Длина каждого нового отрезка вдвое меньше длины предыдущего, то есть за
и т.д. Длина каждого нового отрезка вдвое меньше длины предыдущего, то есть за 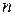 шагов отрезок сократится в
шагов отрезок сократится в 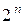 раз. Как только будет выполнено
раз. Как только будет выполнено 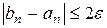 , то в качестве приближенного значения корня, вычисленного с точностью
, то в качестве приближенного значения корня, вычисленного с точностью 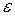 , можно взять
, можно взять 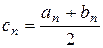 .
.
Пример. Пусть требуется решить уравнение 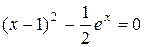 с точностью
с точностью 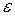 =0,0001. Отделим корень графически. Для этого преобразуем урав-
=0,0001. Отделим корень графически. Для этого преобразуем урав-
|
|
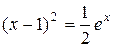 и построим графики функций
и построим графики функций 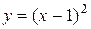 и
и
|
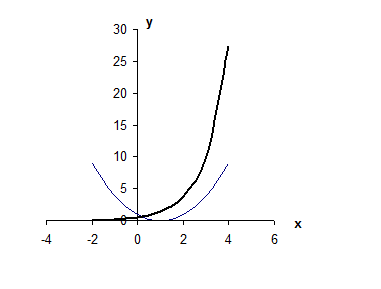
Рис. 4.
Уточнение корня выполним методом половинного деления.
Первый шаг. 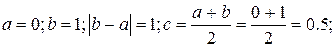
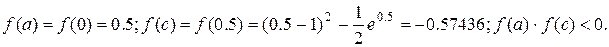
Корень принадлежит отрезку 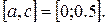
Второй шаг. 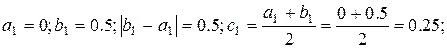
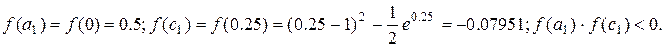 Корень принадлежит отрезку
Корень принадлежит отрезку 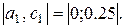
Третий шаг. 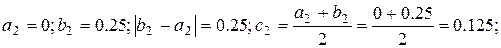
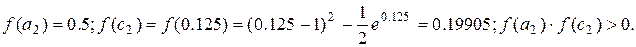
Корень принадлежит отрезку 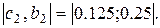
Сведём результаты вычислений в таблицу.
Таблица 1.
| a | b | 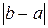
| c | f(a) | f(c) | 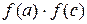
|
| 0.5 | 0.5 | -0.57436 | <0 | |||
| 0.5 | 0.5 | 0.25 | 0.5 | -0.07951 | <0 | |
| 0.25 | 0.25 | 0.125 | 0.5 | 0.19905 | >0 | |
| 0.125 | 0.25 | 0.125 |
Дальнейшие вычисления проведём с помощью программы.
program equation; {Решение уравнения методом половинного деления}
uses crt;
Var
a,b: real; { Концы отрезка }
c: real; { Середина отрезка }
e: real; { Точность }
function f(x: real): real;
Begin
f: = sqr(x-1) - 0.5*exp(x); { Функция f(x) }
end;
Begin
writeln (' Введите концы отрезка: ');
write (' a = '); readln (a);
write (' b = '); readln(b);
write (' Введите точность e = '); readln (e);
writeln(' Результат: ');
while abs (b - a) > 2*e do
Begin
c: = (a + b) / 2;
if f(c) = 0 then
Begin
writeln(' c = ', c: 8: 6, ' f(c) = ', f(c): 8: 6);
readln;
exit;
end;
if f(a) * f(c) < 0 then b: = c else a: = c;
end;
c: = (a + b) / 2;
writeln(' c = ', c: 8: 6, 'f(c) = ', f(c): 8: 6);
readln;
End.
Были введены следующие значения: a = 0, b = 1, e = 0.0001.Получены результаты: с = 0.213287; f (c) = 0.000047.
Ответ: корень уравнения 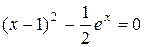 равен 0,2133
равен 0,2133 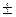 0,0001.
0,0001.
Задания. Найти корень уравнения (если корней несколько, взять наименьший положительный) с точностью 0,0001.
Таблица 2.
| № варианта | Уравнение | № варианта | Уравнение |
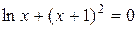
| 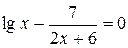
| ||
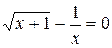
| 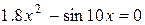
| ||
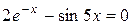
| 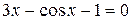
| ||
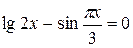
| 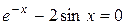
| ||
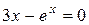
| 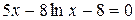
|
2. Решение систем линейных алгебраических уравнений
Системы линейных алгебраических уравнений (СЛАУ) широко используются во многих областях прикладной математики. Оставляя за рамками данной работы вопросы теории линейных систем, отметим, что некоторые СЛАУ могут вообще не иметь решения или иметь бесконечное множество решений. В дальнейшем мы будем рассматривать только системы, имеющие единственное решение.
В общем виде система из n уравнений с n неизвестными выглядит так:
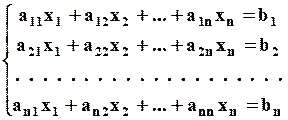
| (2.1) |
Таким образом, даны квадратная матрица коэффициентов при неизвестных { aij }, i, j = 1, 2, …, n, и вектор-столбец свободных членов (правых частей уравнений) { bi }, i = 1, 2, …, n. В результате решения требуется определить n неизвестных x1, x2, …, xn, которые удовлетворяют одновременно всем уравнениям системы.
Все методы решения СЛАУ делятся на две группы – прямые и итерационные. Прямые методы дают решение после выполнения конечного числа операций. Эти методы достаточно универсальны, но в ряде случаев полученное решение не является достаточно точным. Итерационные методы используют последовательные приближения (итерации) к искомому результату. Они позволяют получить решение с любой заданной точностью, но при их использовании заранее неизвестно количество предстоящих итераций, более того, итерационные методы в некоторых случаях вообще не дают решения.
В данном пособии мы рассмотрим по одному методу из каждой группы.
 2015-02-14
2015-02-14 596
596
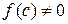 , то в качестве нового отрезка изоляции корня
, то в качестве нового отрезка изоляции корня 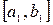 выбираем ту половину
выбираем ту половину 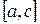 или
или 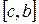 , на концах которой
, на концах которой 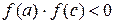 , то корень принадлежит отрезку
, то корень принадлежит отрезку 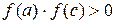 - отрезку
- отрезку 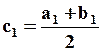 ,
,
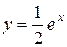
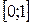 .
Подтвердим аналитически правильность нахождения отрезка изоляции корня. Для отрезка
.
Подтвердим аналитически правильность нахождения отрезка изоляции корня. Для отрезка 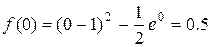 ;
;
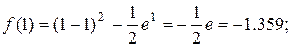
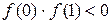 . Следовательно, корень отделён правильно.
. Следовательно, корень отделён правильно.







