Распространим полученные выводы на линию с несколькими нагрузками. Пусть есть ЛЭП с двумя нагрузками (см. рис. 8.3).
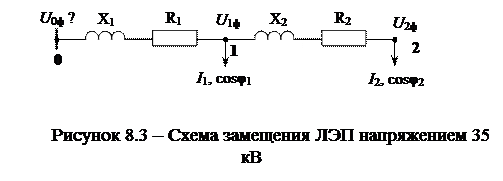 |
Строим векторную диаграмму (см. рис. 8.4). На участке 1-2 построения выполняются вышеизложенному. Получаем треугольник abc – треугольник падения напряжения от тока I 2 в сопротивлениях R 2 и X 2. Соединяем точку 0 с точкой с и получаем фазное напряжение в точке 1. Под углом φ 1 к U 1ф откладываем вектор тока I 1.
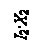  |
По участку 0-1 протекает суммарный ток нагрузок I Σ. Он и создает падение напряжения в сопротивлениях R 1 и X 1. Построим этот вектор. Повторим построения на этом участке и получим треугольник падения напряжения сdf. Соединяем точку 0 с точкой f и получаем фазное напряжение в точке 0. Спроецируем вектор U 0ф на вещественную ось. Отрезок af – продольная составляющая полного падения напряжения на участках 1-2 и 0-1. Отрезок aе, полученный после совмещения векторов U 0ф и U 2ф, – суммарная потеря напряжения на участках ЛЭП.
Считаем:
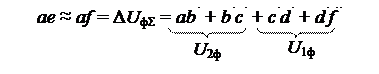 |
Таким образом,
Δ U ф = I2·R2 cos φ2 + I2·X2 sin φ2 + IΣ·R1 cos φ1 + IΣ·X1 sin φ1.
При n нагрузках –
Δ U ф = 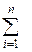 (Ii·Ri cos φi + Ii·Xi sin φi),
(Ii·Ri cos φi + Ii·Xi sin φi),
А при заданных мощностях –
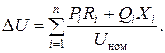
 2015-02-14
2015-02-14 649
649








