Таким образом, уравнения равновесия для фермы примут вид
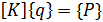 . (4.11)
. (4.11)
Решение системы уравнений (4.8) сводится к вычислению вектора-столбца неизвестных перемещений 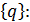
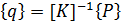 . (4.12)
. (4.12)
Существуют стандартные программы решения системы линейных алгебраических уравнений методом Гаусса без нахождения обратной матрицы к матрице жесткости (SIMQ “Fortrun”).
После решения уравнений (4.11) и нахождения узловых обобщенных перемещений по выражению (4.12) определяются узловые перемещения в локальной системе координат для каждого элемента по соотношению (4.1):
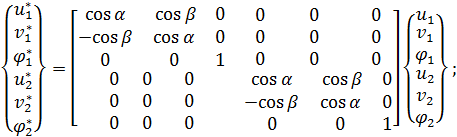 (4.13)
(4.13)
По узловым обобщенным перемещениям можно найти величину относительной деформации, соответствующие нормальной силе 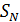 , поперечной силе
, поперечной силе 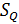 и изгибающему моменту
и изгибающему моменту 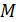 (рис. 4.4):
(рис. 4.4):
Рис. 4.4. Вычисление относительных деформаций
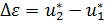 ;
;
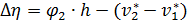 ;
;
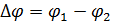 ;
;
Данные соотношения позволяют найти внутренние силы в первом узле:
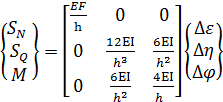 , (4.14)
, (4.14)
где квадратная матрица есть часть локальной матрицы жесткости (левый верхний угол). Столбцы этой матрицы показывают внутренние силы в первом узле при единичном смещении в соответствующем направлении данного узла и жестком закреплении второго узла. Значения двух силовых факторов постоянны по длине элемента 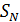 ,
, 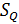 и равны в первом и втором узлах элемента.
и равны в первом и втором узлах элемента.
В соответствии с правилом знаков, по которому при положительном изгибающем моменте растянуты нижние волокна
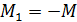
Изгибающий момент во втором узле определим из соотношения:
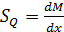 ,
,
и линейного характера изменения изгибающего момент в пределах элемента:
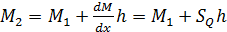 (4.15)
(4.15)
На эпюре моментов ось направлена вниз относительно оси элемента 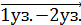
Для решения динамической задачи формируется система уравнений вида:
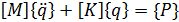 , (4.16)
, (4.16)
в которой глобальная матрица масс 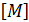 формируется аналогично матрице жесткости путем сложения матриц масс элементов.
формируется аналогично матрице жесткости путем сложения матриц масс элементов.
Поиск частного решения уравнения (4.16), при гармоническом внешнем воздействии 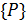 , сводится к заданию выражения для обобщенных перемещений
, сводится к заданию выражения для обобщенных перемещений 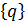 в виде функций, подобных правой части уравнения.
в виде функций, подобных правой части уравнения.
Пусть внешние силы изменяются по закону:
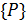 =
= 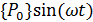 , (4.17)
, (4.17)
тогда произвольное частное решение уравнения (4.16), соответствующее установившемуся режиму представим в виде
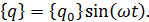 (4.18)
(4.18)
Вторая производная от выражения (4.18) равна
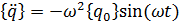
Подставляя выражение (4.15) в уравнение (4.13), получим
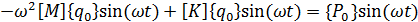
Приравнивая коэффициенты в левой и правой части при 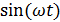 , приходим к линейной системе алгебраических уравнений:
, приходим к линейной системе алгебраических уравнений:
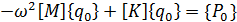 ,
,
вынесем за скобки неизвестные амплитудные значения
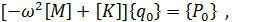 (4.19)
(4.19)
Обозначим
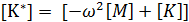 ,
,
тогда уравнение (4.19) становится аналогичным (4.11)
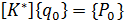 (4.20)
(4.20)
В матрице 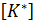 и столбце
и столбце 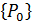 необходимо преобразовать строки, соответствующие перемещениям на которые наложены ограничения (необходимо учесть главные граничные условия), также как это производилось для матрицы [K] при статических расчетах. После система уравнений (4.20) решается с помощью программы, реализующей метод Гаусса, и находятся амплитуды вынужденных колебаний
необходимо преобразовать строки, соответствующие перемещениям на которые наложены ограничения (необходимо учесть главные граничные условия), также как это производилось для матрицы [K] при статических расчетах. После система уравнений (4.20) решается с помощью программы, реализующей метод Гаусса, и находятся амплитуды вынужденных колебаний 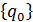 в решении (4.18) для установившегося режима.
в решении (4.18) для установившегося режима.
По амплитудам 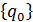 , аналогично статическому решению вычисляют амплитуды внутренних силовых факторов по соотношениям (4.13), (4.14), (4.15).
, аналогично статическому решению вычисляют амплитуды внутренних силовых факторов по соотношениям (4.13), (4.14), (4.15).
Текст клиентского кода программы приведен в ПРИЛОЖЕНИИ 2.
Результаты расчетов представлены на рисунках 4.5, 4.6, 4.7,4.8.
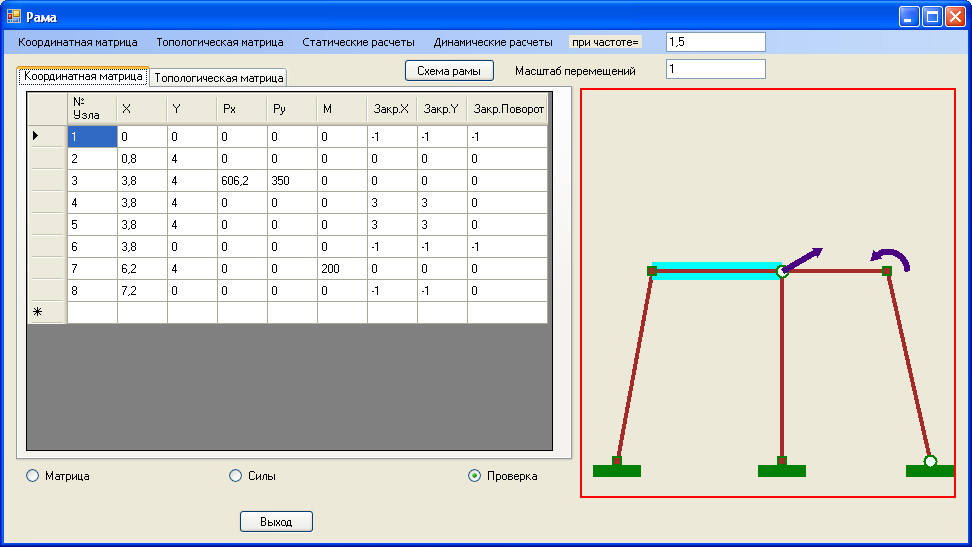
Рис. 4.5 Координатная матрица узлов конструкции и схема расположения элементов.
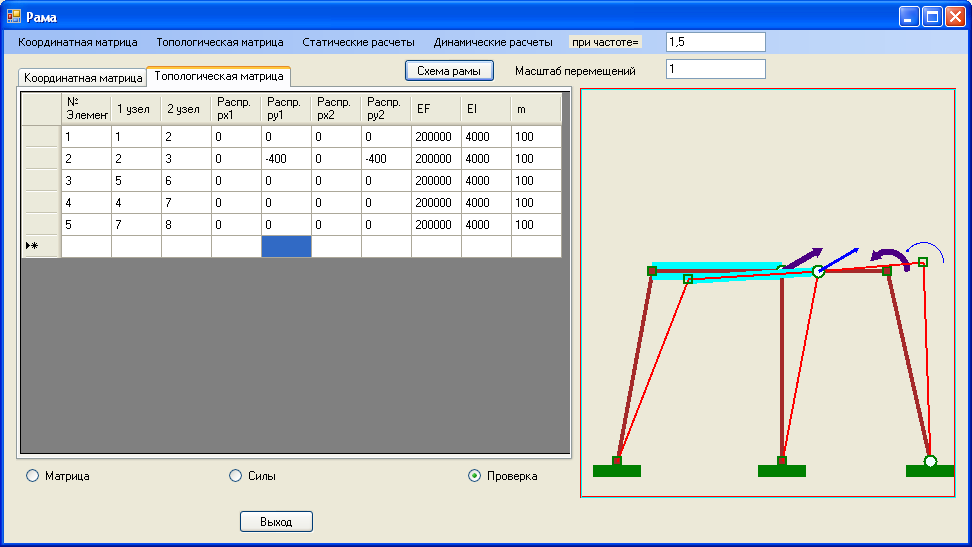
Рис. 4.6 Топологическая матрица элементов конструкции и схема перемещение узлов при статической нагрузке.
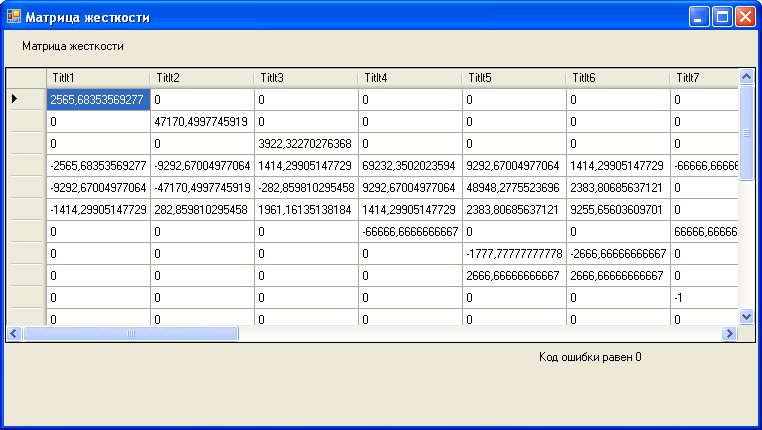
Рис. 4.7. Матрица жесткости конструкции.
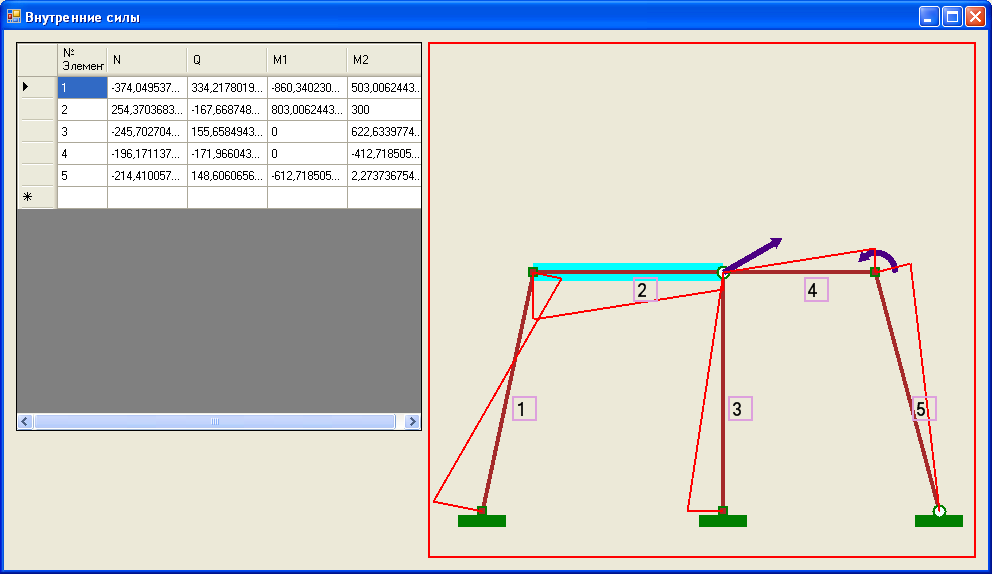
Рис. 4.8. Внутренние силовые факторы при статической нагрузке.
Метод конечных элементов для рамы является приближенным, поэтому точность расчетов, особенно при распределенных нагрузках (элемент №2), зависит от количества узловых точек и шаге разбиения на элементы. Так на участке №2 распределенные силы приводятся к узловым сосредоточенным силам и сосредоточенным парам сил, приложенным на границах элемента. Особенно влияние этих пар сил заметно на эпюре моментов вблизи шарниров, например, этим обусловлен скачёк в конце второго участка перед внутренним шарниром.
Также перераспределяются силы инерции при динамических расчетах в соответствии с коэффициентами матрицы масс. Для повышения точности вычислений целесообразно выполнить разбиение конструкции на большее число элементов, так система рис. 4.2 схема расположения узлов и элементов выглядит, как показано на рис. 4.9.
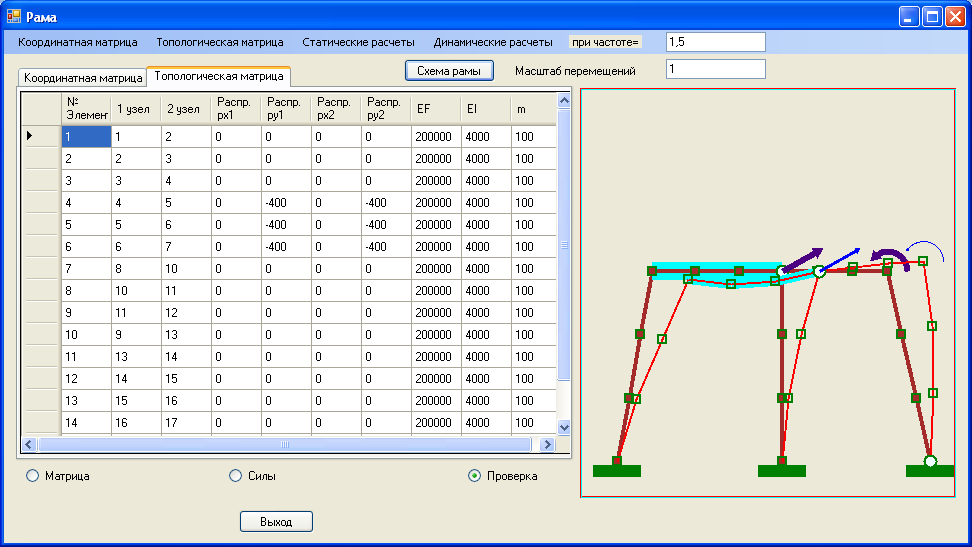
Рис. 4.9 Топологическая матрица элементов конструкции и схема перемещение узлов при статической нагрузке.
На рис.4.10 построены эпюры изгибающих моментов, из которых видно представление в виде ломаной линии на участках №4,5,6, которая заменяет параболу, получаемую при точном решении от действия распределенных сил.
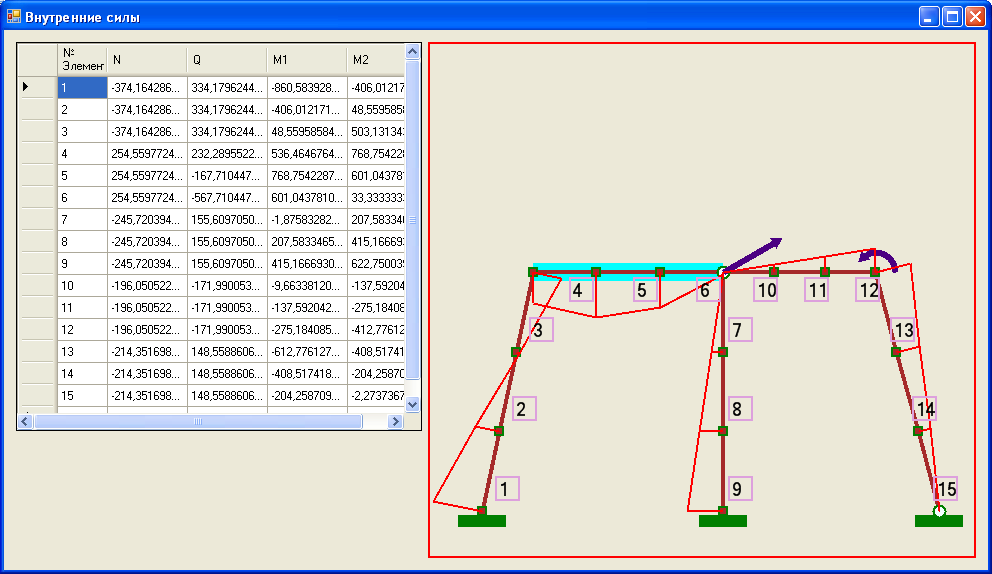
Рис. 4.10. Внутренние силовые факторы, при статическом нагружении.
При тех же амплитудах нагрузки приложенных в динамике с частотой 1,5 рад/с получим амплитудные значения перемещений, представленные на рисунках 4.11.
Внутренние силовые факторы показаны на рисунке 4.12, из которых виден криволинейный характер эпюр изгибающих моментов на прямых участках конструкции, что обусловлено влиянием распределенных сил инерции.
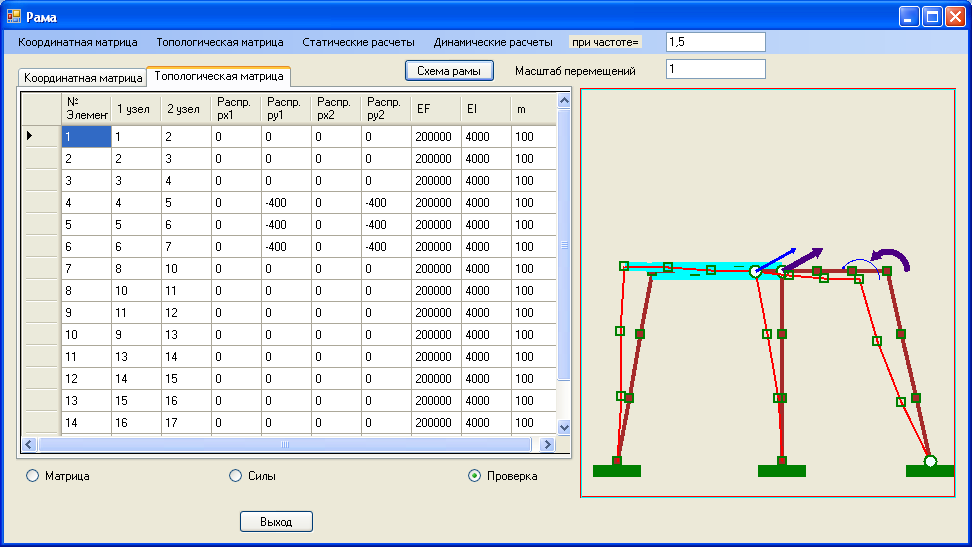
Рис. 4.11 Топологическая матрица элементов конструкции и амплитудные значения перемещений узлов при динамической нагрузке.
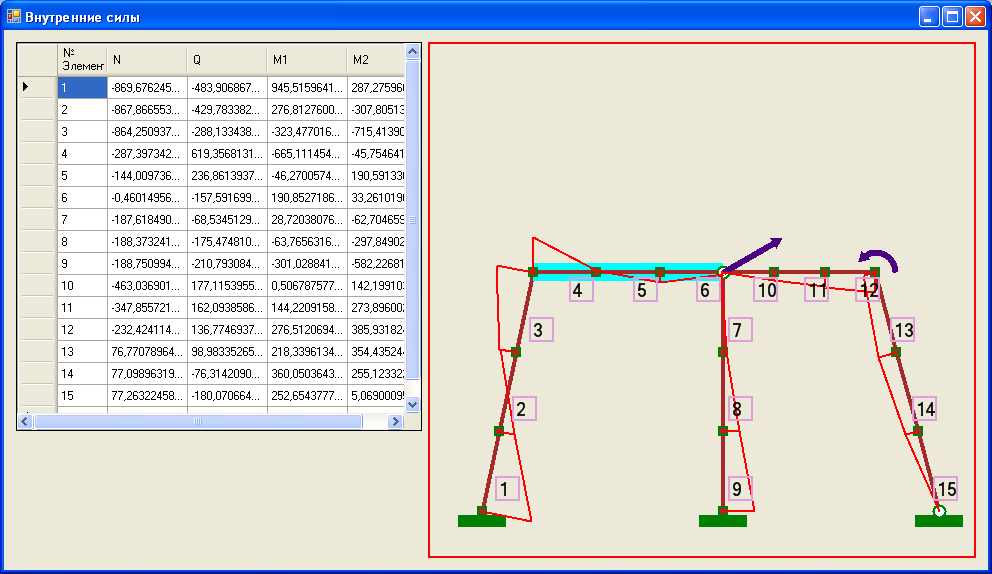
Рис. 4.12. Внутренние силовые факторы при динамическом нагружении.
5. Потенциальное течение несжимаемой жидкости
Потенциальное течение жидкости удовлетворяет условию неразрывности, которое запишется так:
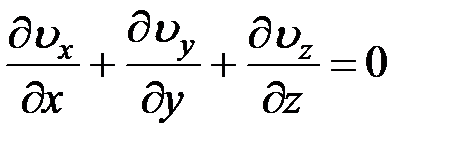 .
.
То есть значения скоростей потока описываются уравнением для невязкой несжимаемой жидкости, для которого возможно записать уравнение Лапласа:
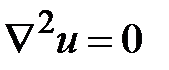 ,
,
где  - оператор Гамильтона,
- оператор Гамильтона, 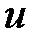 - потенциал скорости.
- потенциал скорости.
Это уравнение имеет вид:
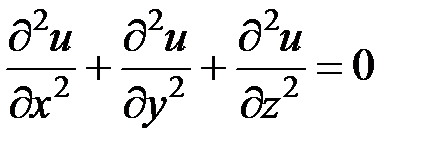 . (5.1)
. (5.1)
В рабочей зоне слой взвешенных частиц или пористого материала, или решетки создают дополнительное сопротивление движению жидкости (или воздуха при малых избыточных давлениях), и течение в этой зоне существенно отличается от остальной области.
Применяется допущение о том, что течение в слое твердых частиц подчинено закону Дарси, который описывает течение в пористых средах:
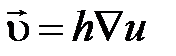 , (5.2)
, (5.2)
где 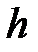 - коэффициент фильтрации, который является функцией плотности пористой среды и свойств потока жидкости. При ламинарном течении в порах существует соотношение для определения коэффициента
- коэффициент фильтрации, который является функцией плотности пористой среды и свойств потока жидкости. При ламинарном течении в порах существует соотношение для определения коэффициента 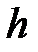 :
:
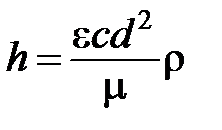 , (5.3)
, (5.3)
где 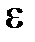 - пористость объема (
- пористость объема (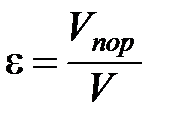 ,
, 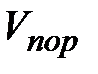 - объем пор;
- объем пор; 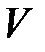 - полный объем);
- полный объем); 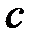 - безразмерный параметр;
- безразмерный параметр; 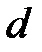 - средний диаметр пор;
- средний диаметр пор; 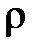 - плотность воздуха.
- плотность воздуха.
Таким образом, плоское течение в пористых средах описывается уравнением Лапласа вида
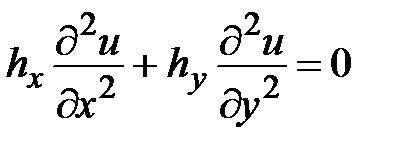 , (5.4)
, (5.4)
где 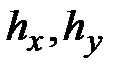 - коэффициенты фильтрации, которые могут быть различными в разных направлениях (например для моделирования решетки с жалюзи).
- коэффициенты фильтрации, которые могут быть различными в разных направлениях (например для моделирования решетки с жалюзи).
Течение в камере в целом может быть описано уравнением (5.4), если коэффициенты 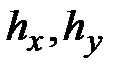 будут различными в разных областях течения. Функция
будут различными в разных областях течения. Функция 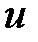 имеет физический смысл величины, пропорциональной избыточному статическому давлению в потоке, взятому с противоположным знаком. Граничные условия для уравнения (5.4) бывают двух типов:
имеет физический смысл величины, пропорциональной избыточному статическому давлению в потоке, взятому с противоположным знаком. Граничные условия для уравнения (5.4) бывают двух типов:
а) главные граничные условия на 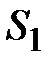 (рис. 5.1) вида
(рис. 5.1) вида 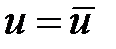 ;
;
б) естественные граничные условия на 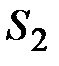 с заданием нормальной составляющей скорости
с заданием нормальной составляющей скорости 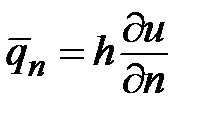 , где
, где 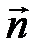 - нормаль к границе.
- нормаль к границе.

Рис. 5.1 Граничные условия в объеме воздуха: 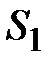 - поверхность с главными;
- поверхность с главными; 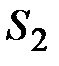 - с естественными граничными условиями.
- с естественными граничными условиями.
 2015-02-14
2015-02-14 585
585








