В методе конечных элементов матрица для всей области течения формируется из матриц отдельных элементов, которые выражаются как функции узловых неизвестных. Последующий учет главных граничных условий приводит к изменениям общей матрицы. Аналогично величины, заданные в узлах элемента, образуют вектор обобщенной узловой нагрузки, разрешая полученную систему уравнений, определяют значения искомой функции в узлах.
Таким образом, основными этапами применения метода являются следующие:
1) дискретизация задачи, то есть представление области 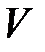 в виде совокупности конечных элементов, взаимосвязанных в узловых точках;
в виде совокупности конечных элементов, взаимосвязанных в узловых точках;
2) получение матриц элементов;
3) построение общей матрицы для всей области и вектора нагрузки;
4) наложение граничных условий;
5) решение системы уравнений;
6) расчет любой другой функции, зависящей от узловых неизвестных.
Первый этап конечно-элементной процедуры состоит в разбиении области потока на ряд элементов. Затем каждый элемент рассматривается отдельно, и его свойства выводятся путем применения формулы метода Галеркина после выбора аппроксимирующих функций. Эти аппроксимирующие функции должны удовлетворять условиям допустимости и полноты для рассматриваемой задачи. Допустимость предполагает непрерывность искомой функции и ее производных между элементами, обеспечивающую корректность определения неизвестных в рамках вариационной формулировки. Условия полноты аппроксимирующих функций должны обеспечить стремление к постоянным производных при уменьшении размеров элемента.
После разбиения области на элементы характерные точки на границах элементов перенумеровывают и называют узлами.
Узлы выбирают в углах конечных элементов (рис. 5.2).
Таблица связности элементов имеет вид:
Таблица 5.1.
Матрица индексов (она же топологическая матрица)
| № элемента | Узел | ||
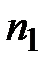 | 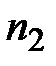 | 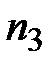 | |
Нумерация узлов проводится в одном и том же направлении, например, против хода часовой стрелки. Если аппроксимируется одна функция (потенциал скоростей), то полученная таблица является матрицей индексов решаемой задачи.

Рис. 5.2 Схема разбиения области на три треугольных конечных элемента
На рисунке 5.2 показаны глобальные номера узлов. Введем также локальную нумерацию, которая в таблице 5.1 соответствует буквам 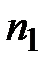 ,
, 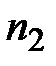 ,
, 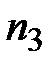 (рис. 5.3).
(рис. 5.3).
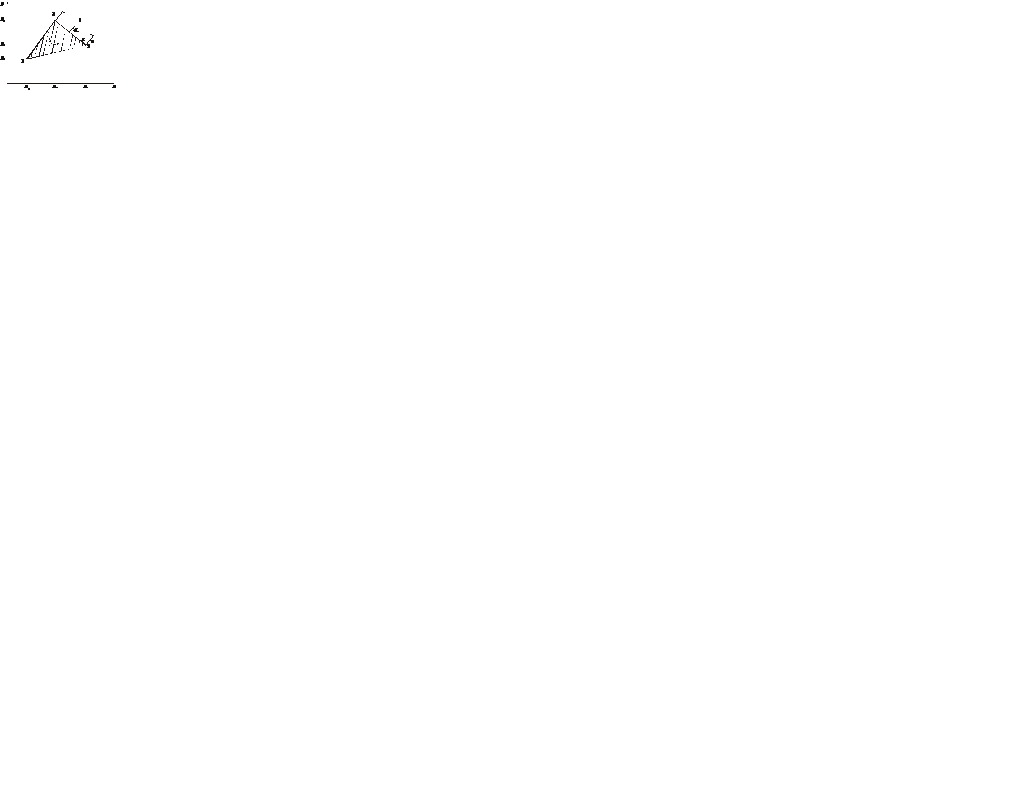
Рис. 5.3. Локальные номера узлов
На втором этапе метода конечных элементов проводится аппроксимация неизвестной функции 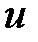 базисными функциями
базисными функциями 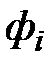 :
:
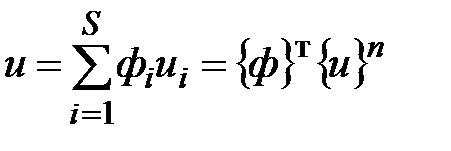 , (5.5)
, (5.5)
где 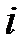 - номер узла в местной системе; для треугольного элемента с тремя узлами
- номер узла в местной системе; для треугольного элемента с тремя узлами 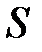 =3;
=3;
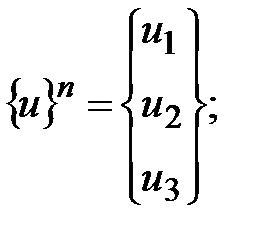 (5.6)
(5.6)
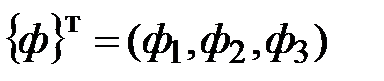 .
.
Введем соответствующие матрицы конечных элементов для гармонического уравнения Лапласа (5.1) с граничными условиями обоих типов:
1) 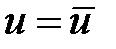 на
на 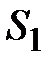 ;
;
2) 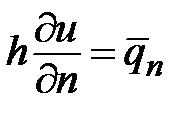 на
на 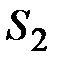
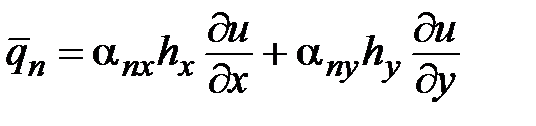 ,
,
где 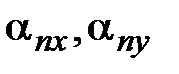 - направляющие косинусы нормали к
- направляющие косинусы нормали к 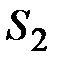 .
.
Если выбранная аппроксимирующая функция удовлетворяет условию 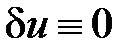 на
на 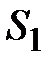 , где
, где 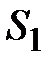 может быть частью внешней границы области
может быть частью внешней границы области 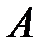 , то воспользовавшись вариационной формулировкой метода Галеркина, можно записать:
, то воспользовавшись вариационной формулировкой метода Галеркина, можно записать:
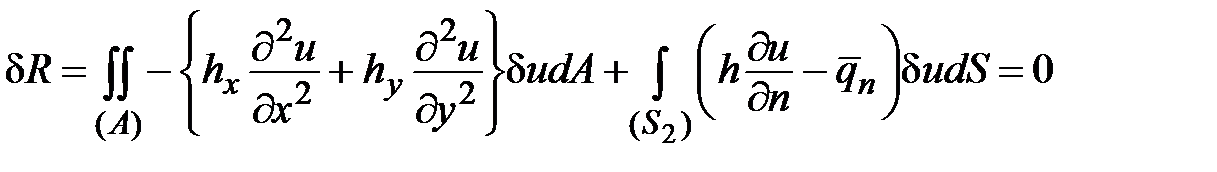 .
.
Интегрируя это уравнение по частям, приходим к выражению
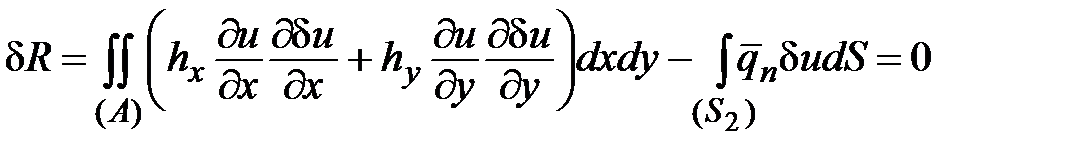 .
.
Выражение в левой части есть вариация функционала
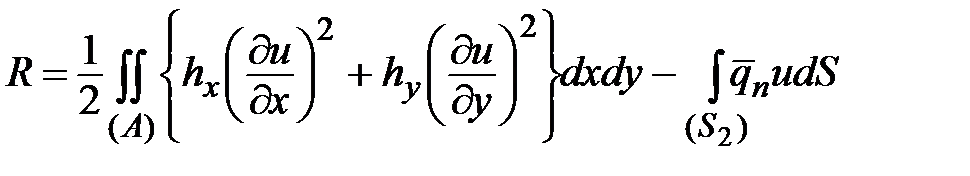 .
.
Закон изменения 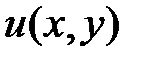 по полю конечного элемента аппроксимируем степенным полиномом вида
по полю конечного элемента аппроксимируем степенным полиномом вида
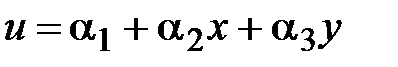 . (5.7)
. (5.7)
Входящие в формулу неизвестные параметры 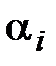 можно выразить через узловые значения в узловых точках 1, 2, 3. Для угловых узлов получим
можно выразить через узловые значения в узловых точках 1, 2, 3. Для угловых узлов получим
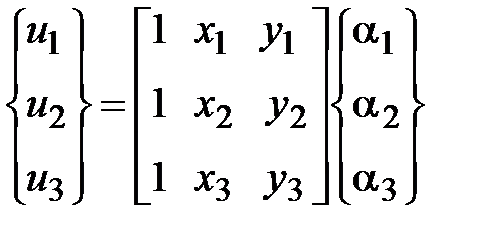
или в матричной форме
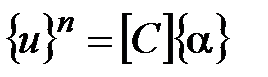 .
.
Отсюда
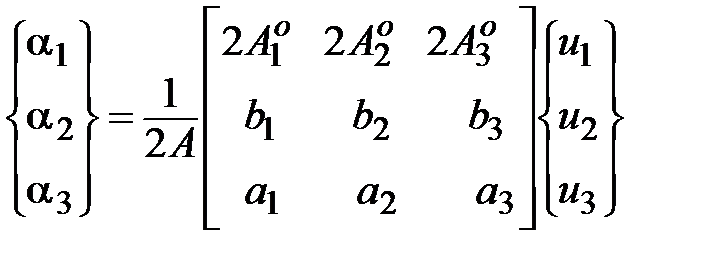 , (5.8)
, (5.8)
иначе 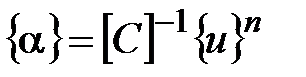 ,
,
где 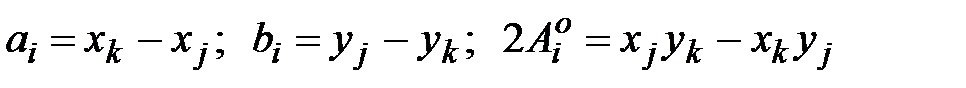 при
при 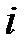 =1, 2, 3;
=1, 2, 3;  =2, 3, 1;
=2, 3, 1; 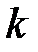 =3, 1, 2;
=3, 1, 2; 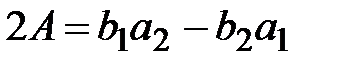 , причем
, причем  - площадь элемента.
- площадь элемента.
Используя зависимости (5.7) и (5.8), получим следующие выражения для производных функции 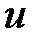 :
:
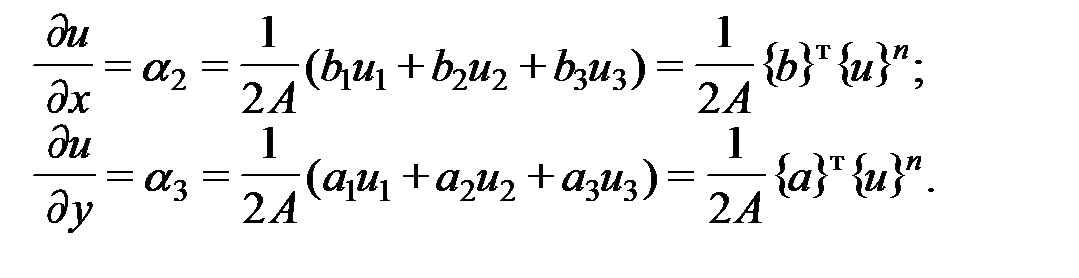 (5.9)
(5.9)
и для производных от вариаций:
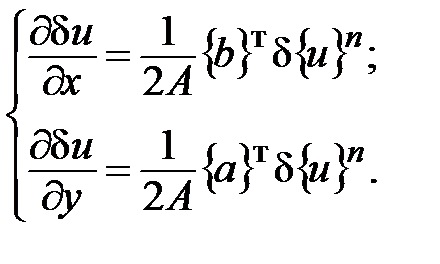 (5.10)
(5.10)
Исключая из выражения (5.7) с помощью (5.9) параметры 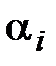 , находим
, находим
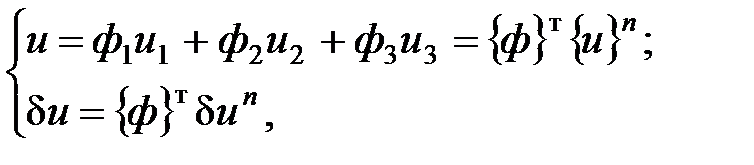 (5.11)
(5.11)
где 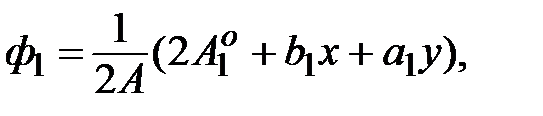
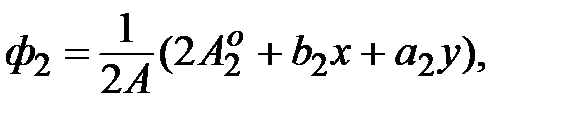
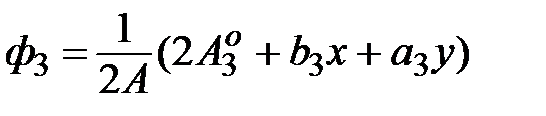 ,
,
есть базисные функции для треугольного элемента. Подстановка выражений (5.9), (5.10), (5.11) в вариационную формулировку метода Галеркина дает
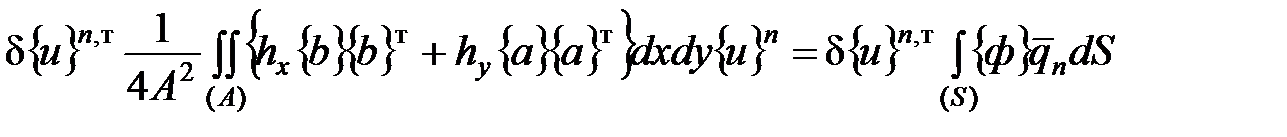 . (5.12)
. (5.12)
После интегрирования левая часть уравнения (5.12) приводится к виду
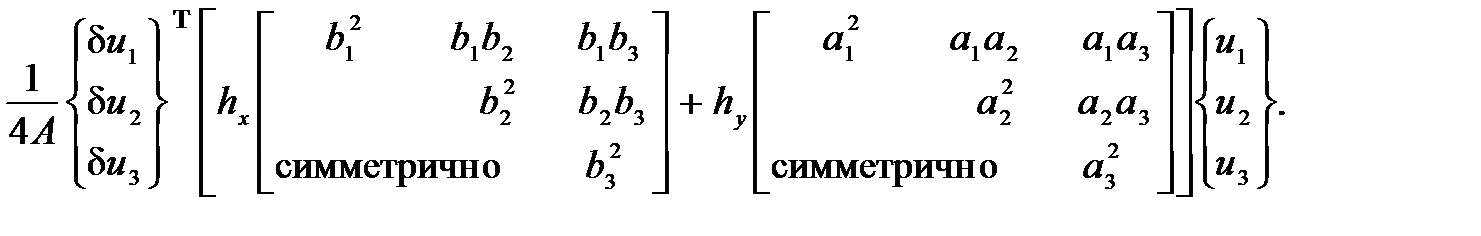 (5.13)
(5.13)
Выражение (5.13) в компактной форме имеет вид:
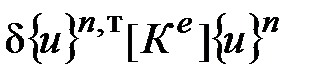 , (5.14)
, (5.14)
где 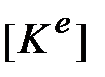 - матрица коэффициентов влияния для треугольного элемента, состоящая в выражении (5.13) из двух слагаемых, стоящих в квадратных скобках.
- матрица коэффициентов влияния для треугольного элемента, состоящая в выражении (5.13) из двух слагаемых, стоящих в квадратных скобках.
Если коэффициенты фильтрации 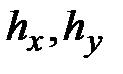 различны (при наличии жалюзи и сеток) и местные оси координат
различны (при наличии жалюзи и сеток) и местные оси координат 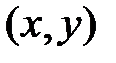 не совпадают по направлению с глобальными осями координат, то матрицу коэффициентов влияния
не совпадают по направлению с глобальными осями координат, то матрицу коэффициентов влияния 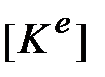 можно вычислить в местной системе координат, а затем объединить с матрицами других элементов при сборке глобальной матрицы
можно вычислить в местной системе координат, а затем объединить с матрицами других элементов при сборке глобальной матрицы 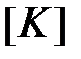 . При этом, кроме координат узлов элемента и коэффициентов
. При этом, кроме координат узлов элемента и коэффициентов 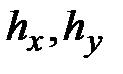 , для таких элементов необходимо задать угол поворота локальных осей координат.
, для таких элементов необходимо задать угол поворота локальных осей координат.
Правая часть равенства (5.12) существует только на части 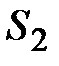 границы области. Предположим, что величина
границы области. Предположим, что величина 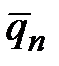 постоянна, например, на стороне 2-3 (рис.5.3) Связь между координатами
постоянна, например, на стороне 2-3 (рис.5.3) Связь между координатами 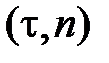 и
и 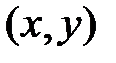 такова
такова
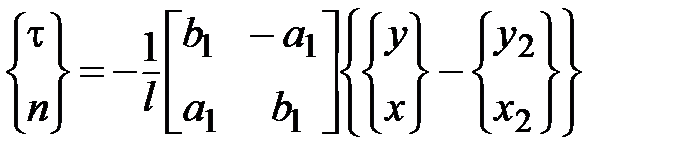 .
.
Тогда для интеграла по 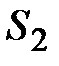 в правой части (5.12) имеем:
в правой части (5.12) имеем:
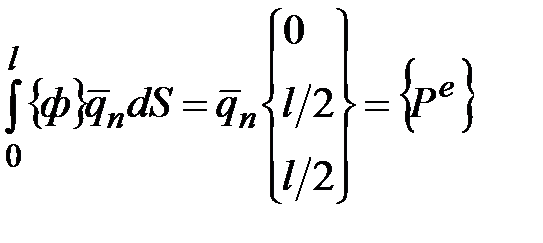 . (5.15)
. (5.15)
Из выражений (5.15), (5.13) по уравнению (5.12) следует
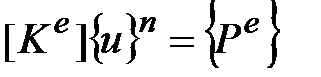 . (5.16)
. (5.16)
Это алгебраическое уравнение связывает узловые значения искомой функции через матрицу коэффициентов влияния с потоком воздуха на границе области.
На третьем этапе конечно-элементной процедуры производят объединение матриц коэффициентов влияния 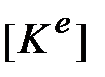 для всей исследуемой области в матрицу
для всей исследуемой области в матрицу 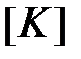 . Размер этой матрицы определяется числом узловых неизвестных для всей области. Для области из трех элементов, показанной на рисунке 5.1 матрица
. Размер этой матрицы определяется числом узловых неизвестных для всей области. Для области из трех элементов, показанной на рисунке 5.1 матрица 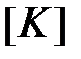 будет иметь размер 5´5.
будет иметь размер 5´5.
Формирование ее проводят с помощью матрицы индексов (табл. 5.1). Организуется цикл по элементам (по строкам матрицы индексов), содержимое ячейки 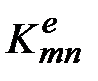 каждого элемента добавления в ячейку
каждого элемента добавления в ячейку 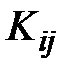 глобальной матрицы коэффициентов влияния, причем номера
глобальной матрицы коэффициентов влияния, причем номера 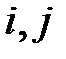 берутся из строки матрицы индексов,
берутся из строки матрицы индексов, 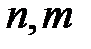 - это локальные номера того же элемента.
- это локальные номера того же элемента.
Аналогично формируется глобальный вектор нагрузки 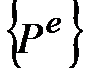 .
.
Таким образом, система уравнений для области в целом имеет вид
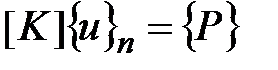 , (5.17)
, (5.17)
где 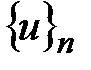 - глобальные узловые неизвестные.
- глобальные узловые неизвестные.
На четвертом этапе накладываются граничные условия. Эта операция выполняется для узловых переменных, в которых известны значения искомой функции.
Чтобы не изменять порядок системы уравнений (5.17) преобразуем матрицу 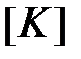 и столбец
и столбец 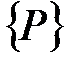 полагая, что граничное условие первого типа задано в узле
полагая, что граничное условие первого типа задано в узле 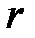 :
:
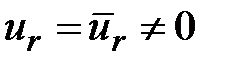
при 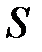 =1, 2, …,
=1, 2, …, 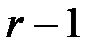
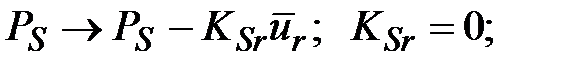
при 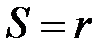
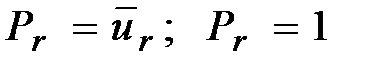 ;
;
при 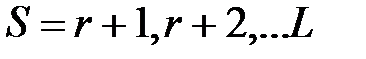
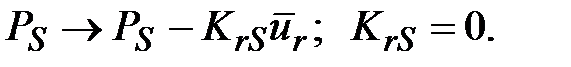
На пятом этапе решается система уравнений, например методом Гаусса. После решения системы уравнений (5.17), в которой учтены граничные условия, можно определить скорости потока
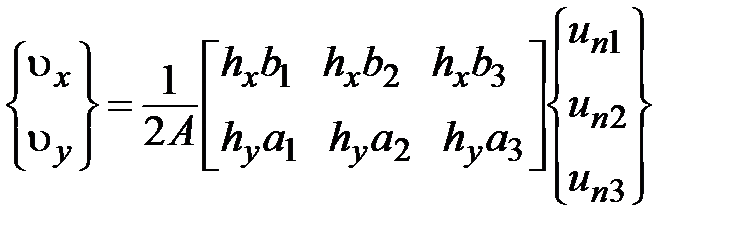 . (5.18)
. (5.18)
С помощью приведенных отношений можно вычислить  для всех элементов, причем в данном случае эти величины постоянны в пределах каждого из элементов. Если коэффициенты фильтрации
для всех элементов, причем в данном случае эти величины постоянны в пределах каждого из элементов. Если коэффициенты фильтрации 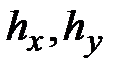 задавались в локальной системе отсчета, как и коэффициенты
задавались в локальной системе отсчета, как и коэффициенты 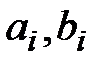 , то полученные скорости
, то полученные скорости  необходимо спроецировать на оси глобальной системы отсчета, используя матрицу поворота, состоящую из направляющих косинусов локальных осей.
необходимо спроецировать на оси глобальной системы отсчета, используя матрицу поворота, состоящую из направляющих косинусов локальных осей.
По изложенному алгоритму составлены программы на алгоритмическом языке "C#", приведенные в ПРИЛОЖЕНИИ 3.
На рисунках 5.4, 5.5, 5.6, 5.7, 5.8. показан пример расчета потенциального течения несжимаемой жидкости на плоскости с графическим представлением исходных данных.
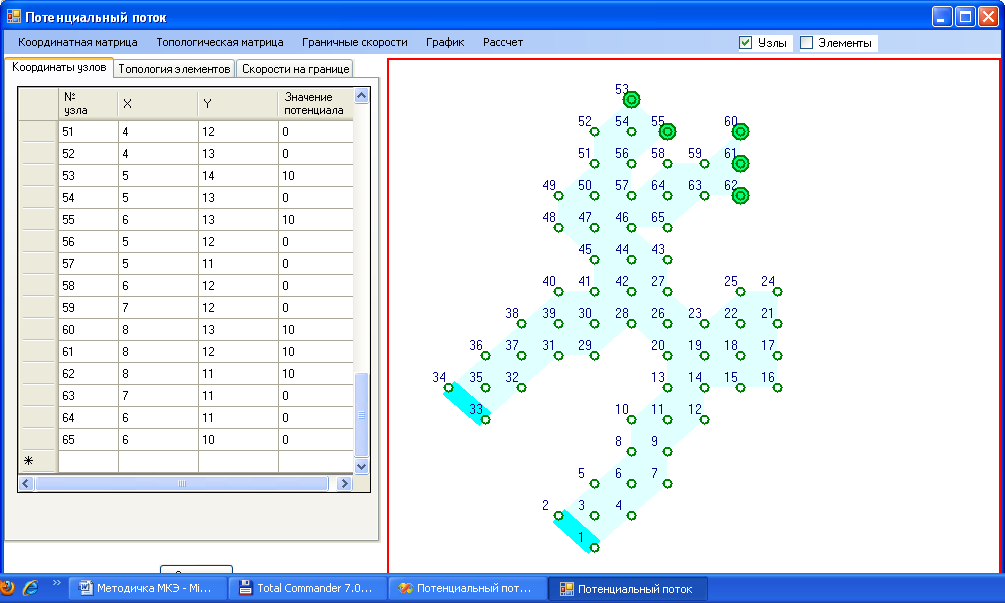
Рис. 5.4 Схема расположения узлов.
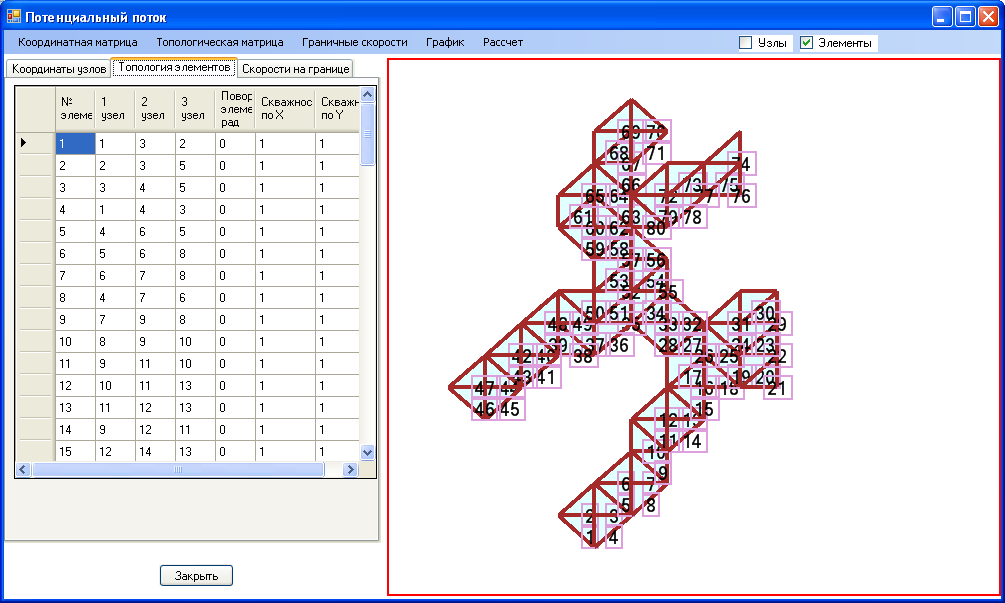
Рис. 5.5 Разбиение области течения на треугольные конечные элементы.
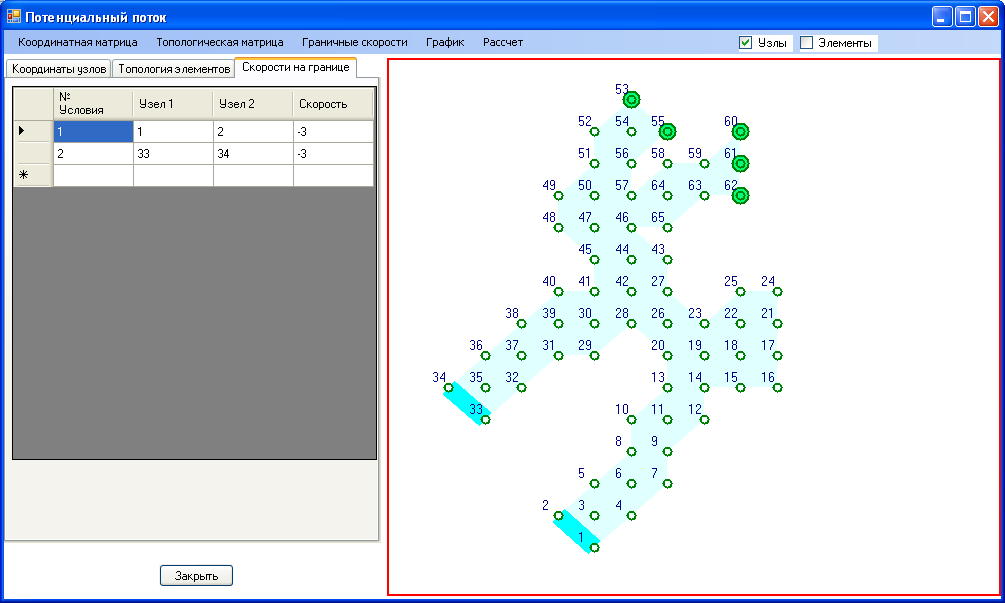
Рис. 5.6 Наложение граничных условий (скорости на границе отмечены на отрезках широкой сплошной линией – узлы 33-34; 1-2, заданные в координатной матрице потенциалы скоростей обозначены кругами в узлах 53, 55, 60, 61, 62 значение потенциала скоростей равно 10 в последнем столбце таблицы на рис. 5.4).
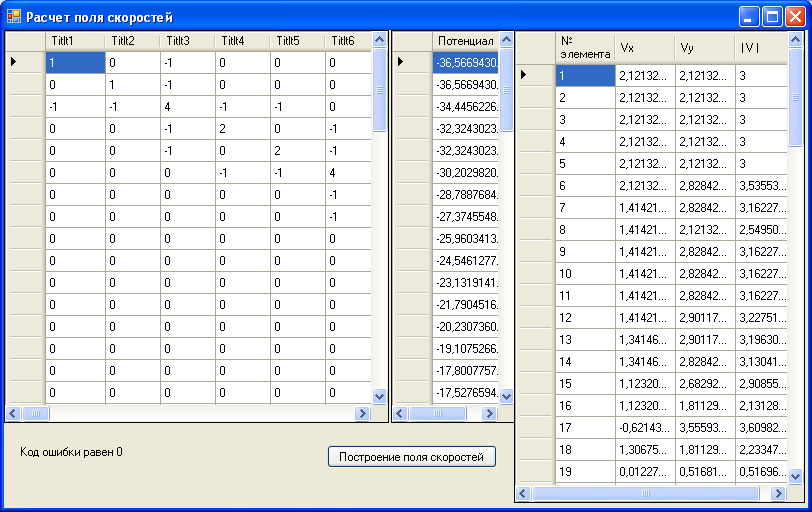
Рис. 5.7 Матрица коэффициентов влияния, значения потенциала скоростей в узлах и скорости в каждом конечном элементе.
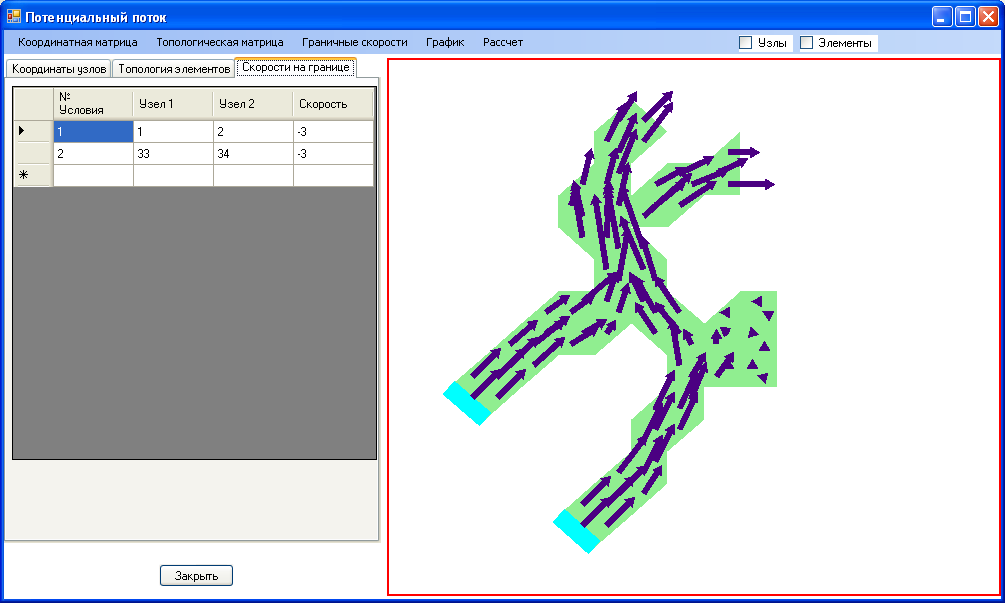
Рис. 5.8 Распределение поля скоростей при плоском течении жидкости.
 2015-02-14
2015-02-14 1178
1178
