Приборы и принадлежности: электросекундомер, выпрямитель, маятник, стальной шарик, секундомер, линейка.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ:
1. Знать законы свободного падения.
2. Знать методы определения ускорения свободного падения
методом математического маятника.
3. Разобраться в принципе работы электросекундомера.
4. Уметь выводить формулы: 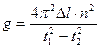 и
и 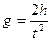
II метод: Метод математического маятника.
В физике под маятником понимают твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной точки или оси. Различают физический и математический маятник.
Математическим маятником называют идеализированную систему, состоящую из невесомой и нерастяжимой нити, на которой подвешена масса, сосредоточенная в одной точке. Хорошим приближением к математическому маятнику служит небольшой шарик, подвешенный на длинной тонкой нити. Отклонение маятника от положения равновесия будем характеризовать углом (φ), образованным нитью с вертикалью. При отклонении маятника от положения равновесия возникает вращательный момент (М), равный по величине (mglsinφ), (m- масса, l- длина маятника).
M=mglsinφ. Напишем для маятника уравнение динамики вращательного движения M=Iε. Угловое ускорение 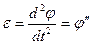 и, учитывая, что момент инерции маятника равен ml2, получим:
и, учитывая, что момент инерции маятника равен ml2, получим:
ml2φ//=-mglsinφ, приведем к виду: 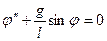 . При малых колебаниях sin φ ≈ φ. Введем обозначение:
. При малых колебаниях sin φ ≈ φ. Введем обозначение: 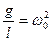 , тогда получим
, тогда получим 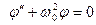 . Следовательно, при малых колебаний угловые отклонения маятника изменяются со временем по гармоническому закону. Известно, что
. Следовательно, при малых колебаний угловые отклонения маятника изменяются со временем по гармоническому закону. Известно, что 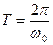 с учетом того что
с учетом того что 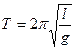 , отсюда можно найти
, отсюда можно найти 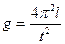 где l- длина маятника от точки подвеса до центра масс. Центр массы шарика определяется путем дополнительных расчетов, которые приводят к увеличению погрешностей, чтобы избежать этого можно пользоваться формулой:
где l- длина маятника от точки подвеса до центра масс. Центр массы шарика определяется путем дополнительных расчетов, которые приводят к увеличению погрешностей, чтобы избежать этого можно пользоваться формулой: 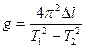 которая получается, если записать период колебаний для длинного и короткого маятника и решить систему относительно g;
которая получается, если записать период колебаний для длинного и короткого маятника и решить систему относительно g; 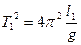 ;
; 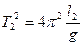 .
.
В этом случае нас интересует только Δl, которую можно определить (измерить) как расстояние между двумя положениями любой точки шарика. Для определения периода колебания подсчитывают время n колебаний, затем, поделив общее время на число колебаний, находят период Т, время одного колебания. Если для обеих длин брать одинаковое число колебаний, то формулу для определения ускорения свободного падения можно записать: 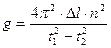 .
.
 2015-02-14
2015-02-14 443
443








