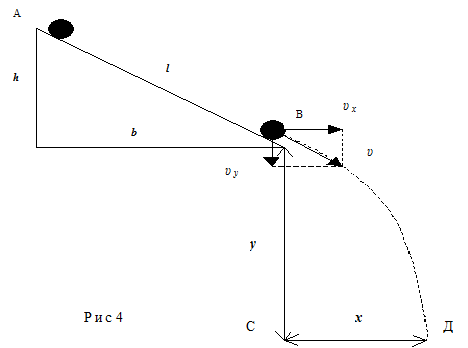
Исследуемое тело (шар, сплошной цилиндр, полый цилиндр) в точке А обладает запасом потенциальной энергии Ep=mgh. В точке В тело приобрело кинетическую энергию поступательного движения 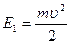 и вращательного движения
и вращательного движения 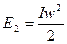 (рис 4).
(рис 4).
По закону сохранения энергии: 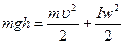 . В данной работе скорость υ тела в точке В находят экспериментальным путем и теоретически по формуле (1). Определить скорость тела теоретически можно из закона сохранения энергии и соотношения
. В данной работе скорость υ тела в точке В находят экспериментальным путем и теоретически по формуле (1). Определить скорость тела теоретически можно из закона сохранения энергии и соотношения 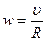 . Получим формулу:
. Получим формулу: 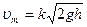 где
где 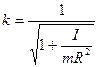 . (R) - радиус испытуемого тела, w - его угловая скорость в точке В. При вычислении скорости следует брать момент инерции:
. (R) - радиус испытуемого тела, w - его угловая скорость в точке В. При вычислении скорости следует брать момент инерции:
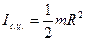 - для сплошного цилиндра.
- для сплошного цилиндра.
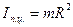 - для тонкостенного полого цилиндра.
- для тонкостенного полого цилиндра.
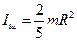 - для шара.
- для шара.
Подставляя значения I находят значения k для всех тел. Из формулы (1), зная высоту наклонной плоскости, определяют скорость υт.
Экспериментальное определение скорости проводят следующим образом. В точке В тело имеет скорость, проекции которой в горизонтальном и вертикальном направлениях равны: 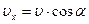 ,
, 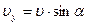 (рис. 4). Отрезки х и у могут быть определены из законов поступательного движения. В нашем случае
(рис. 4). Отрезки х и у могут быть определены из законов поступательного движения. В нашем случае 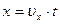 ;
; 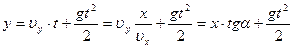
(3); где х - горизонтальное перемещение СД тела, у - путь проходимый телом по вертикали ВС.
Время перемещения тела по СД и ВС одинаково и равно 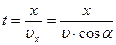 , отсюда искомая величина скорости
, отсюда искомая величина скорости 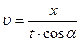 (4). Из формулы (3) найдем время
(4). Из формулы (3) найдем время 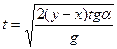 (5) и подставим в формулу (4). После подстановки получим окончательное выражение для определения скорости тела экспериментальным путем:
(5) и подставим в формулу (4). После подстановки получим окончательное выражение для определения скорости тела экспериментальным путем: 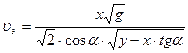 .
.
 2015-02-14
2015-02-14 514
514








