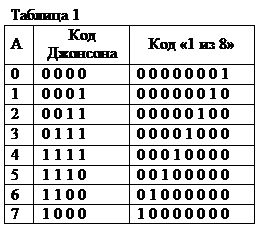
Последовательность чисел в этом коде моделируется односторонним последовательным заполнением его разрядов вначале единицами, а затем нулями. Результат представления десятичного числа А в коде Джонсона представлен в таблице 1.
 Код «I из m»
Код «I из m»
Последовательность чисел в этом коде моделируется появлением единицы в том разряде, десятичный номер которого равен (А + 1), начиная с младшего разряда. Результат представления десятичного числа А в коде «I из m» для m = 8 представлена в таблице 1.
Количество разрядов, требуемое для представления числа А в рассмотренных недвоичных кодах уже не определяется выражением (2.4), а должно выбираться исходя из возможного однозначного соответствия числу А его кодовой комбинации.
2.2. КЛАССИФИКАЦИЯЯ И ПОСТАНОВКА ЗАДАЧИ
СИНТЕЗА ЦИФРОВЫХ АВТОМАТОВ
В соответствие с определением цифрового автомата и способом кодирования цифровой информации можно считать, что на вход автомата поступает множество комбинаций двоичных переменных 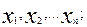 а с выхода снимается множество двоичных переменных
а с выхода снимается множество двоичных переменных 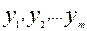 (в общем случае n ¹ m), каждая из которых может принимать два значения: 0 или 1.
(в общем случае n ¹ m), каждая из которых может принимать два значения: 0 или 1.
|
|
|
По характеру связи входных и выходных переменных с учетом их изменения по тактам работы, цифровые автоматы делятся на комбинационные (КЦА) и последовательностные.
КЦА – это устройство, совокупность 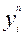 - выходных сигналов которого в дискретные моменты времени однозначно определяется входными сигналами
- выходных сигналов которого в дискретные моменты времени однозначно определяется входными сигналами 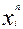 , поступавшими на вход в те же дискретные моменты времени. Здесь индекс n означает номер дискретного интервала времени (называемого тактом) работы КЦА.
, поступавшими на вход в те же дискретные моменты времени. Здесь индекс n означает номер дискретного интервала времени (называемого тактом) работы КЦА.
Таким образом, КЦА не содержит элементов памяти, и их функционирование описывается системой функций:
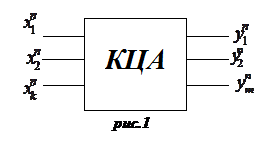
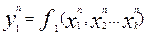
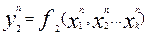 (2.8)
(2.8)
……………………….
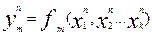
И задача синтеза КЦА сводится к построению системы (2.8) и реализации полученных логических функций в заданном элементом базисе. При таком подходе удобным математическим аппаратом для синтеза КЦА является булева алгебра или алгебра логики, ставящая в соответствие истинному высказыванию – двоичную переменную х =1, а ложному – двоичную переменную х = 0.
2.3. ОСНОВНЫЕ ТОЖДЕСТВА И ФУНКЦИИ
АЛГЕБРЫ И ЛОГИКИ (ФАЛ)
В основе алгебры логики лежат три логические операции над такими переменными:
1. Инверсия (логическое отрицание) – обозначается чертой, которая ставится над переменной: 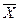 ; читается НЕ Х.
; читается НЕ Х.
2. Дизъюнкция (логическое сложение) – обозначается: Х1 + Х2 (для двух переменных); читается Х1 или Х2.
3. Конъюнкция (логическое умножение) – обозначается: Х1 × Х2 (для двух переменных); читается Х1 иХ2.
Постулативно, предполагается, что при выполнении перечисленных операций отношения эквивалентности имеют вид:
|
|
|
ИЛИ И НЕ
0 + 0 = 0 0 × 0 = 0
1 + 0 = 1 1 × 0 = 0 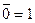
0 + 1 = 1 0 × 1 = 0
1 + 1 = 1 1 × 1 = 1 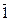 = 0
= 0
На основании этих постулатов можно вывести основные тождества алгебры логики:
Х + 1 = 1; x × 0 = 0; 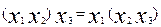
Х + 0 = Х; x + 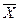 = 1;
= 1; 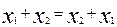 ;
;
Х + Х = Х; Х × 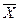 = 0;
= 0; 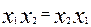 ;
;
Х × Х = Х; 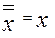 ;
;
Х × 1 = Х; 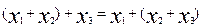 ;
;
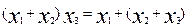 ;
;
Особое значение для синтеза КЦА, в случае необходимости использования данного базиса, имеют следующие тождества:
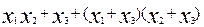 ;
;
2. Теорема Моргана (верна и в случае n – переменных):
а) 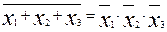 ;
;
б) 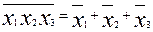 ;
;
в) 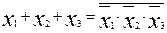 ; (2.9)
; (2.9)
г) 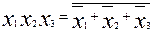 ;
;
3. 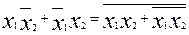 , доказываемое путем применения теоремы Моргана к правой или левой части.
, доказываемое путем применения теоремы Моргана к правой или левой части.
Булевой функцией (или ФАЛ) называется двоичная переменная у, значение которой зависит от значений других двоичных переменных (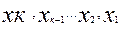 ), именуемых аргументами:
), именуемых аргументами:
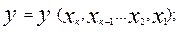 (2.10)
(2.10)
В этом выражении все переменные могут принимать одно из двух значений: 0 или1. Задание булевой функции означает, что каждому из возможных наборов (комбинаций) значений ее аргументов поставлено в соответствие определенное значение у. Поскольку каждый аргумент может принимать лишь одно из двух значений, то общее количество комбинаций Р из к двоичных аргументов составит:
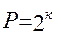 ; (2.11)
; (2.11)
Возможные комбинации значений двух, трех, четырех входных аргументов имеют вид (таблица 2):
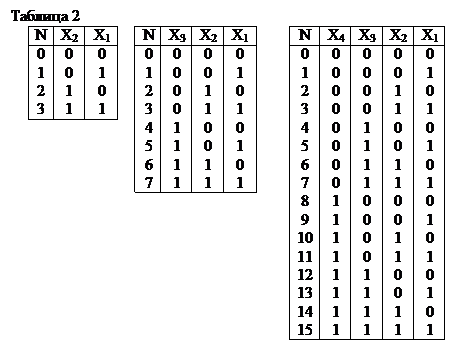 Здесь удобно комбинации обозначать в виде представления десятичного числа N в двоичной системе счисления.
Здесь удобно комбинации обозначать в виде представления десятичного числа N в двоичной системе счисления.
Скажем N = 12 = 1100.
В алгебре логики показано, что F - общее количество различных функций от к двоичных аргументов определяется выражением:
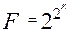 (2.12) Естественно, практическая реализация такого большого числа функций в виде логических элементов (микросхем) затруднительна. Можно показать, что существует система логических функций (набор логических элементов), позволяющая представить любую сколь угодно сложную функцию (построить сколь угодно сложный цифровой автомат). Такая система функций называется функционально полной системой логических функций, а набор логических элементов, ей соответствующий – функционально полным набором (ФПН).
(2.12) Естественно, практическая реализация такого большого числа функций в виде логических элементов (микросхем) затруднительна. Можно показать, что существует система логических функций (набор логических элементов), позволяющая представить любую сколь угодно сложную функцию (построить сколь угодно сложный цифровой автомат). Такая система функций называется функционально полной системой логических функций, а набор логических элементов, ей соответствующий – функционально полным набором (ФПН).
Один из возможных ФПН, схемотехническое обозначение логических элементов, и реализуемые логические функции приведены на рис.2 (для двух переменных).
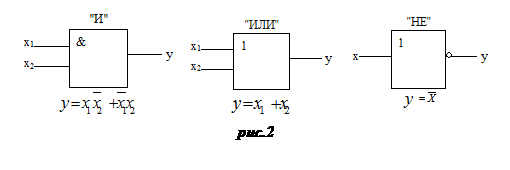 Используя их суперпозицию можно построить любую логическую функцию. Например, функция неравнозначности двух аргументов имеет вид:
Используя их суперпозицию можно построить любую логическую функцию. Например, функция неравнозначности двух аргументов имеет вид:
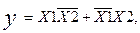 (2.13)
(2.13)
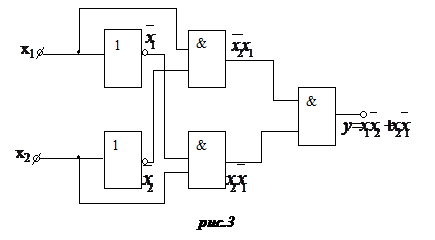
а устройство, реализующее ее, представлено на рис.3.
 В составе современных серий интегральных микросхем имеются и другие ФПН, в виде так называемой двухступенчатой логики, когда один элемент выполняет последовательно две логические операции.
В составе современных серий интегральных микросхем имеются и другие ФПН, в виде так называемой двухступенчатой логики, когда один элемент выполняет последовательно две логические операции.
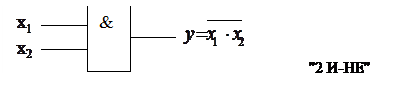 |
Элемент Шеффера (И-НЕ), для двух переменных имеет вид:
 |
Элемент Пирса (ИЛИ-НЕ), для переменных имеет вид:
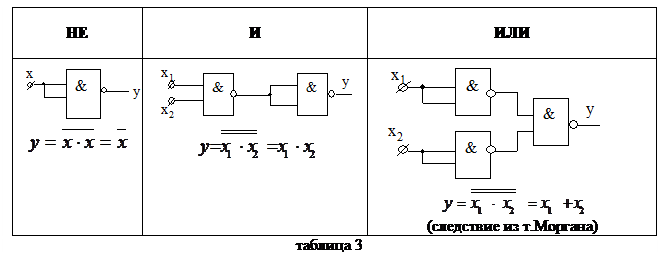
Для доказательства их функциональной полноты, покажем что из каждого из них можно получить базис (набор) И, ИЛИ, НЕ.
Результаты приведены в таблице 3.
На практике часто используются элементы многоступенчатой логики, выполняющие последовательно не две, а несколько операций.
 |
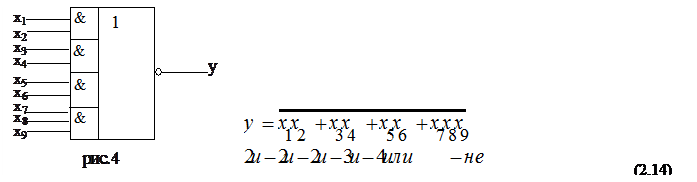 |
Например: микросхема К155ЛР3 (рис.4)
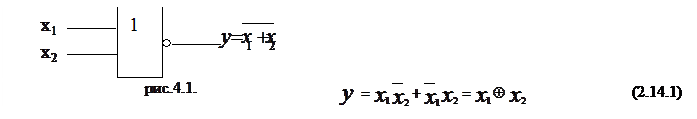 Например: микросхема К155ЛП5 (рис.4.1)
Например: микросхема К155ЛП5 (рис.4.1)
Сравнивая (2.6) и (2.13) можно отметить их тождественность. Таким образом, сумматор по модулю 2 является цифровым дискрименатером, реагирующим на совпадение (неравнозначность) входных переменных.
Т.е. у = 1 тогда и только тогда x1≠x2 и y = 0, когда x1=x2
2.4. СПОСОБЫ ЗАДАНИЯ ФАЛ
Существует 3 формы (способа) задания булевых функций.
1.Словесный способ.
При этом способе задания функция определяется словами, причем описание должно однозначно определять все случаи, в которых выходные сигналы принимают значение 0 или1.
Пример: Функция равна единице, если любые два (и только два) из трех ее аргументов равны единице, и нулю во всех остальных случаях.
2.Табличный способ.
Способ задания булевых функций с помощью таблиц истинности (функционирования), представляющих собой некоторую таблицу, в которой отмечены все возможные наборы (комбинации) входных переменных (см. табл.2)и значения функции на каждом наборе.
|
|
|
Пример: Для функции, заданной выше словесным способом, таблица истинности будет иметь вид: (табл.4)
Под аналитическим способом задания булевых функций подразумевается запись функций в виде алгебраического выражения.
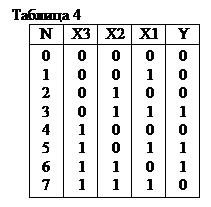 Пример:
Пример: 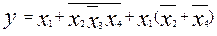
При этом существует две формы аналитической записи функций. Перед описанием необходимо ввести некоторые вспомогательные функции называемые минтермами и макстермами.
Минтерм – булевая функция, принимающая значение «единица» только на одном из наборов аргументов, и равная «нулю» на всех остальных.
Количество минтермов заданного числа аргументов К, как следует из определения, равно числу 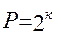 ; возможных комбинаций их значений.
; возможных комбинаций их значений.
Правило аналитической записи минтермов – записывается в виде произведения всех аргументов, причем в прямой форме в него войдут аргументы, имеющие в рассматриваемом наборе значение минтерм для I – го набора: 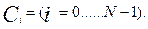
Ниже приведены все минтермы для трех аргументов (из табл.4)

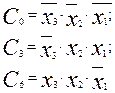
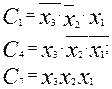
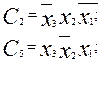 (2.15)
(2.15)
Примечание: в данной работе рассматривается синтез КЦА с использованием только аналитической записи функций в виде суммы минтермов.
Если аналитическое выражение функции У содержит сумму минтермов, то говорят, что она записана в совершенной дизьюктивно-нормальной форме (СДНФ). Если же в некоторых произведениях отсутствуют отдельные переменные, то говорят о дизьюнктивно – нормальной форме (ДНФ).
Пример: ДНФ: 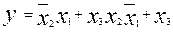 ;
;
СДНФ: 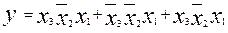 .
.
Каждая логическая функция может быть задана любым их перечисленных способов, однако в конкретных случаях оказывается один из способов и поэтому необходимо переводить функции из одного способа задания к другому.
Переход от табличного способа задания к аналитическому базируется на основной теореме булевой алгебры, утверждающей: любую логическую функцию можно представить в виде суммы произведений значений функции У(N) на каждом из N наборов входных аргументов и соответствующего минтерма:
|
|
|
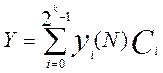 , где (2.16)
, где (2.16)
к- число аргументов функции У;
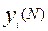 - значение функции У на I-ом наборе;
- значение функции У на I-ом наборе;
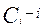 -ый минтерм
-ый минтерм
Пример: Переходя от табличного (см. табл.4) задания функции к аналитическому, получим (с учетом (2.15))
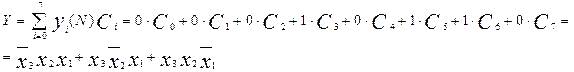

Переход от аналитического задания к табличному может быть осуществлен путем подстановки в выражение функции всех 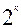 возможных комбинаций входных аргументов и определению, с использованием тождеств алгебры логики, значения функции на этих наборах.
возможных комбинаций входных аргументов и определению, с использованием тождеств алгебры логики, значения функции на этих наборах.
2.5. МИНИМИЗАЦИЯ ФАЛ
Необходимость минимизации продемонстрируем на примере синтеза КЦА, функционирование которого определяется таблицей 5.
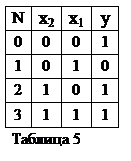 Из 2.16 получаем СДНФ функции:
Из 2.16 получаем СДНФ функции:
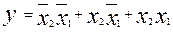 (2.17)
(2.17)
В то же время, выражение (2.17) можно упростить, используя распределительный закон:
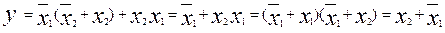 (2.18)
(2.18)
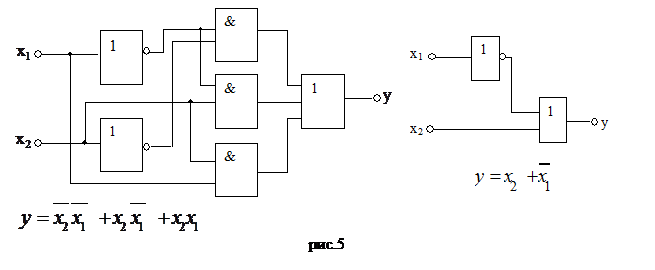
По выражениям (2.17), (2.18) реализуем два варианта КЦА:
(рис.5) в базисе И, ИЛИ, НЕ
Схема устройства построенного по выражению (2.18), реализует ту же функцию существенно меньшим числом логических элементов. Такое устройство будет экономичней и дешевле, следовательно, перед реализацией КЦА логическую функцию необходимо упростить или минимизировать. Строгое решение задачи минимизации должно учитывать, кроме того, коэффициенты объединения и разветвления логических элементов, число их в корпусе микросхемы, стоимость каждого корпуса и т.д. Известные в настоящее время математические методы упрощения в таком объеме задачу не решают. В данной работе изучается способность минимизации ФАЛ по следующему критерию:
Критерий минимизации - получение (тем или иным способом ДНФ функции с минимальным числом вхождений аргументов из исходной СДНФ функции.
При рассмотрении методов минимизации ФАЛ, большее значение имеет понятие смежных минтермов – т.е., отличающихся формой вхождения только одной переменной (в один минтерм переменная входит в прямой форме, в другой - в инверсной).
Пример: соседние минтермы 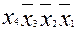 и
и 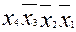 .
.
Метод Кванта
Метод основан на последовательном применении к функции в СДНФ тождеств булевой алгебры и следующих двух операций:
а) склеивания
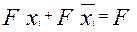 (2.19)
(2.19)
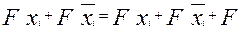 (2.20)
(2.20)
б) поглощения
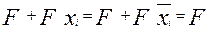 , где (2.21)
, где (2.21)
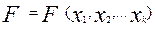 - некоторая функция К аргументов.
- некоторая функция К аргументов.
Пример: минимизировать функцию.
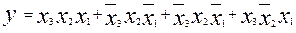
Смежные минтермы здесь 1 и 4; 1 и 2; 2 и 3. Производя склеивание (т.е. применяя вначале 2.19, а затем 2.21) минтермов 1 и 4 получим:
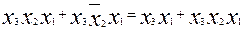
и склеиваем его со вторым минтермом
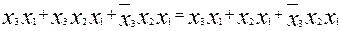
склеиваем второй и третий минтермы:
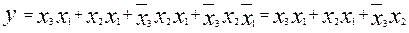 ,
,
получив таким образом ДНФ, следовательно дальнейшее упрощение невозможно. На практике иногда полученную функцию требуется перевести с помощью тождеств булевой алгебры в требуемый базис.
Метод Вейча – Карно
Метод является геометрической иллюстрацией метода Квайна и основан на представлении минимизируемой функции в виде диаграмм Вейча или Корт Карно, облегчающих операцию склеивания за счет того, что смежные минтермы оказываются в геометрической близости друг от друга. Диаграммы Вейча представляют собой прямоугольные таблицы, разделенные горизонтальными и вертикальными линиями на ячейки, общее число которых совпадает с числом минтермов или возможных комбинаций аргументов. В каждую ячейку заносится значение одного минтерма, причем размещение последних осуществляется таким образом, чтобы два смежных минтерма (сравните с (2.19)) находились в соседних ячейках. Такой порядок размещения минтермов обеспечивается принятым способом образования наборов аргументов, соответствующих различным ячейкам диаграммы.
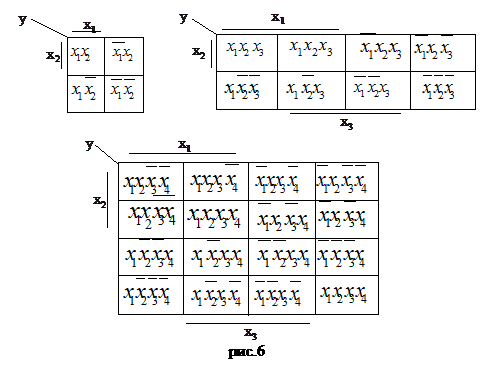 На рис.6 приведены примеры диаграммы Вейча для двух, трех, четырех (переменных), а также показано соответствие ячеек и минтермов.
На рис.6 приведены примеры диаграммы Вейча для двух, трех, четырех (переменных), а также показано соответствие ячеек и минтермов.
Здесь линиями, рядом с обозначение переменных, обозначены зоны вхождения соответствующей переменной в прямой форме, во всех других ячейках эта переменная входит в инверсной форме.
Алгоритм минимизации
1. Отметить единицей те ячейки диаграммы Вейча, которые соответствуют минтермам, входящим в СДНФ минимизируемой функции, либо присутствуют в табличном ее задании и на которых значение функции равно 1. Остальные ячейки либо остаются незаполненными, либо отмечаются нулями.
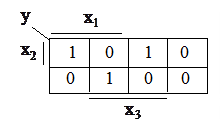 Пример: для функции заданной таблично (табл.4) имеем диаграмму Вейча.
Пример: для функции заданной таблично (табл.4) имеем диаграмму Вейча.
2. Считывается и записывается минимизированная функция по следующим правилам:
а). Минимизированная функция равна сумме (по числу контуров) произведения только тех переменных, которые входят в данный контур, не меняя знака (т.е. либо только в прямой, либо только в инверсной форме);
б). В контур можно объединить только 1,2,4,8 …2 к единиц, причем они должны составлять строку, столбец (или их часть), прямоугольник или квадрат, либо быть расположенными симметрично, относительно хотя бы одной из осей диаграммы Вейча;
в). В контур необходимо стремиться объединить возможно большее количество единиц, при этом упрощается аналитическое выражение;
г). Контурами должны охватываться все без исключения единицы, и ни в один контур не должен быть включен нуль;
д). Одна и та же единица может быть включена в несколько контуров;
е). Число контуров должно быть минимально.
При невыполнении хотя бы одного из пунктов а) – е) задача минимизации считается нерешенной.
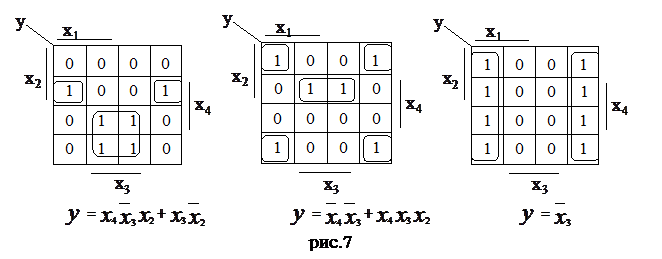 |
На рис. 7 показаны возможные варианты объединения единиц и получающиеся функции для некоторых случаев:
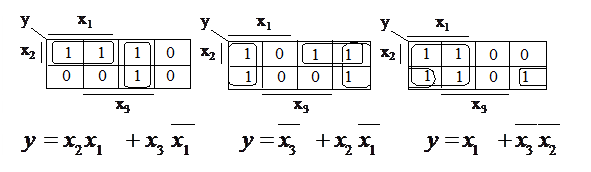 |
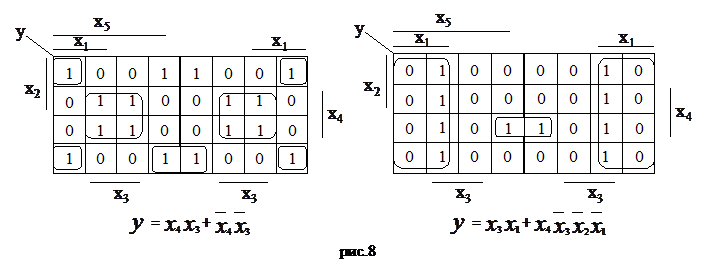
В случае 5 переменных диаграмма Вейча допускает осевую симметрию относительно двух дополнительных вертикальных осей (рис.8).
Пример:
2.6. НЕКОТОРЫЕ СПОСОБЫ МИНИМИЗАЦИИ ФАЛ.
МИНИМИЗАЦИЯ «ПО НУЛЯМ»
Выше был рассмотрен способ считывания минимизированных функций, заключающийся в объединении в контуры тех ячеек диаграммы Вейча, где функция определена единицей. Однако возможно объединение по тем же правилам ячеек, где функция определена нулем. В этом случае получается минимальная ДНФ инвертированной функции.
Этот способ особенно удобен при синтезе КЦА на элементах многоступенчатой логики (рис.4) типа 155ЛР3, т.к. минимизированная функция сразу приобретает вид (2.14).
Пример:
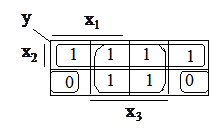 Минимизация «по единицам»
Минимизация «по единицам»
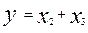
Минимизация «по нулям»
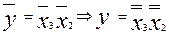
Можно показать (по т.Моргана), что функции, полученные двумя способами тождественно равны.
Минимизация частино-определенных функций
Под частино- определенными функциями понимают функции, которые определены не на всех наборах входных аргументов. Комбинации, на которых функция не определена, называются избыточными или запрещенными. Такая ситуация может иметь место, если избыточные комбинации не возникают при работе синтезируемого КЦА или когда значение функции на избыточной комбинации может быть любым (задаваемым произвольно). Тогда функция доопределяется на избыточных комбинациях таким образом, чтобы минимальная ДНФ имела наименьшее число вхождений аргументов.
Рассмотрим пример использования факультативного доопределения частично-определенной функции.
На рис.9 входная функция задана в виде таблицы, где крестиком обозначены значения функции, которые соответствуют запрещенным комбинациям аргументов. Данные комбинации отражаем на диаграмме Вейча крестиком. При минимизации доопределяем функцию таким образом, чтобы вся функция покрывалась минимальным числом наибольших по размерам контуров (в данном случае двумя контурами по четыре единицы).
Необходимо заметить, что полученная функция Уд определена уже на всех комбинациях так, как это представлено в правом столбце таблицы на рис.9.
2.7. МЕТОДИКА СИНТЕЗА КЦА
При проектировании схем КЦА целесообразно придерживаться следующей методики:
1. Кодирование входных и выходных переменных и переход от словесного задания функции к табличному;
2. Переход от табличной формы задания к СДНФ;
3. Минимизация СДНФ и получение минимальной ДНФ;
4. Переход функции из ДНФ в структурный вид в используемом базисе (из числа имеющихся в наличии логических элементов или микросхем);
5. Составление схем устройства.
В качестве примера рассмотрим задачу синтеза КЦА, задаваемого следующим словесным описанием. Имеется три датчика, выходные сигналы которых являются двоичными. Используя базис «И - НЕ», необходимо обеспечить индикацию состояний, когда единичные значения принимают по меньшей мере два сигнала из трех. В соответствии с методикой имеем:
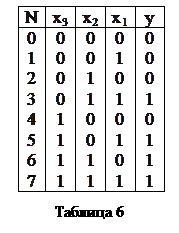 1.Чило входных переменных КЦА, очевидно, равно трем (x3,x2,x1); выходная переменная – одна (У). Значения y=1 соответствуют наборам Х3Х2Х1, в которых две или три переменные равны 1, на остальных наборах у=0. Задаем функционирование таблично (табл.6).
1.Чило входных переменных КЦА, очевидно, равно трем (x3,x2,x1); выходная переменная – одна (У). Значения y=1 соответствуют наборам Х3Х2Х1, в которых две или три переменные равны 1, на остальных наборах у=0. Задаем функционирование таблично (табл.6).
2.Переходим к СДНФ, пользуясь основной теоремой алгебры логики:
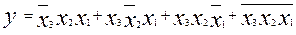
3. Минимизируем полученную СДНФ методом Вейча-Карно:
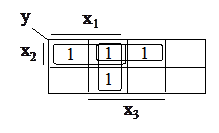
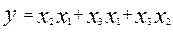
4. Переводим полученную ДНФ в базис «И – НЕ», пользуясь теоремой Моргана (2.9)
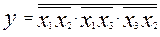
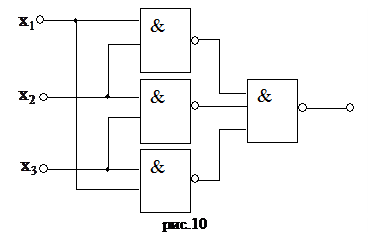
5. На основе этого выражения изображаем схему КЦА (рис.10)
 |
2.8. ЦИФРОВЫЕ УСТРОЙСТВА КОМБИНИРОВАННОГО
ТИПА. ПРЕОБРАЗОВАТЕЛИ КОДОВ
В общем виде это КЦА, осуществляющие преобразование какого – либо кода входного числа в другой (в общем случае произвольный) код на выходе. В качестве примера рассмотрим синтез преобразователя числа из натурального двоичного кода
8-4-2-1 (см. (2.3)) в двоично-десятичный код 2-4-2-1. Последовательность синтеза аналогична изложенной в п.2.7, поэтому приведем лишь окончательные результаты:
1. Таблица функционирования преобразователя (табл.7). Поскольку из условия следует, что число разрядов входного и выходного кодов совпадают. В тоже время, максимальные числа, которые можно записать в этих кодах - различны, в коде 8-4-2-1 это 15=1111, в коде 2-4-2-1- это 9. Следовательно, для 6 комбинаций входного кода, значения выходных функций будут не определены, т.е. избыточны (см. п.2.6).
В тех случаях, когда разрядность выходного кода не задана (например, код Джонсона), ее надо определить как минимально-необходимую для получения взаимно – однозначного соответствия входной и выходной кодовой комбинаций.
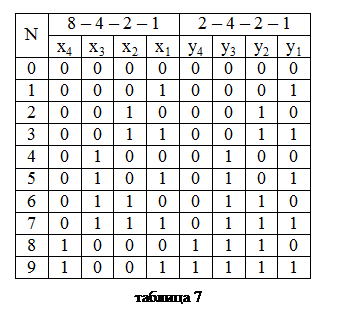
2. Для каждой из выходных переменных составляем диаграмму Вейча:
yi =yi (x4,x3,x2,x1), (i=1,2,3,4), доопределяем избыточные комбинации и считываем минимизированную ДНФ:
|
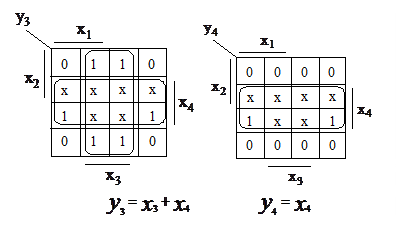
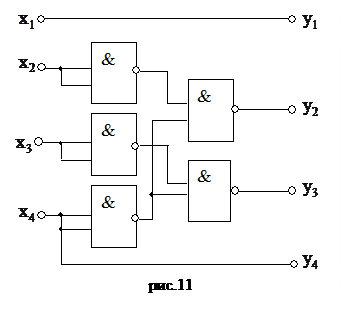
Переводя y2,y3 в требуемый базис (например «2И-НЕ»). Получаем схему преобразователя (рис.11).
Шифратор является одной из широко применяемых на практике разновидностей преобразователя кодов. В этом случае входным кодом является код «1 из m»(см. табл.1), а выходным – натуральный двоичный код 8-4-2-1.
Рассмотрим пример синтеза 4-х разрядного шифратора, т.е. преобразователя кодов «1 из 4» в код «2-1», на двух микросхемах К155ЛР3 (рис.4).
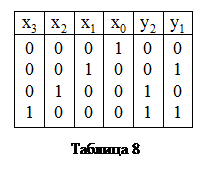 1.Для составления таблицы функционирования (табл.8) заметим, что входной 4-х разрядный код «1 из 4» (табл.1) имеет всего 4 возможные комбинации, то для его отображения кодом 8-4-2-1 потребуется к=2 разряда (т.к. 22 = 4), т.е. два младших разряда 2-1.
1.Для составления таблицы функционирования (табл.8) заметим, что входной 4-х разрядный код «1 из 4» (табл.1) имеет всего 4 возможные комбинации, то для его отображения кодом 8-4-2-1 потребуется к=2 разряда (т.к. 22 = 4), т.е. два младших разряда 2-1.
Как и в предыдущем случае замечаем, что поскольку выходные функции У1,У2 являются функциями 4-х аргументов, для которых возможно 16 комбинаций, в диаграмме Вейча возникает 16-4=12 избыточных комбинаций.
2.Составляем диаграмму Вейча для каждой выходной переменной, доопределяем избыточные комбинации (отмеченные крестиком) и, учитывая то, что схему требуется реализовать на микросхеме К155ЛР3, проводим минимизацию «по нулям».
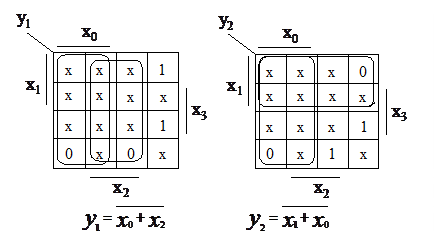
При синтезе КЦА на микросхемах многоступенчатой логики необходимо иметь в виду следующее:
1).При использовании одного их трех (нескольких) входов по «И», два оставшихся желательно соединять с тем, на который подается входной сигнал (при этом увеличивается помехоустойчивость схемы);
 2). При отсутствии каких – либо сигналов на входах микросхем, на этих входах имеется потенциал логической единицы, что приводит, в силу (2.14) к тому, что при yº0 при произвольных входных сигналах. Следовательно, на незадействованные входы в пределах одного элемента «2И» надо подавать уровень логического нуля (т.е. заземлять).
2). При отсутствии каких – либо сигналов на входах микросхем, на этих входах имеется потенциал логической единицы, что приводит, в силу (2.14) к тому, что при yº0 при произвольных входных сигналах. Следовательно, на незадействованные входы в пределах одного элемента «2И» надо подавать уровень логического нуля (т.е. заземлять).
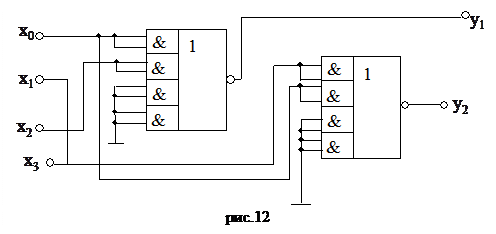
С учетом этого схема приобретет вид (рис.12).
Обратите внимание, что вход Х3 оказался никуда не подключенным, что очевидно, т.к. ни функция y1, ни функция y2 от переменной x3 не зависят, она не входит в их аналитические выражения.
 ис.12
ис.12
Дешифратор выполняет функции обратные функциям шифраторов, т.е. осуществляет преобразование входного числа, представленного в каком-либо коде, в код «1 из m». В случае входного кода 8-4-2-1 работа дешифратора приобретает простой физический смысл: единица на выходе проявляется только в том разряде (во всех остальных – нули), десятичный номер которого равен входной кодовой комбинации. Рассмотрим синтез дешифратора, преобразующего двухразрядное число N из кода «2-1» в код «1 из 4».
1. Составляем таблицу функционирования. Соображения по выбору числа разрядов входного кода аналогичны приведенным при синтезе шифратора.
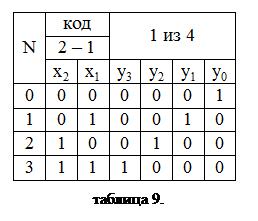 2.Анализ табл.9 показывает, что каждая из выходных функций У1-У4 принимает единичное значение только на одном из наборов входных переменных, следовательно, в диаграмме Вейча окажется заполненной только одна ячейка и минимизация будет невозможна. Таким образом составлять диаграмму Вейча нет необходимости, а аналитические выражения следуют из (2.16):
2.Анализ табл.9 показывает, что каждая из выходных функций У1-У4 принимает единичное значение только на одном из наборов входных переменных, следовательно, в диаграмме Вейча окажется заполненной только одна ячейка и минимизация будет невозможна. Таким образом составлять диаграмму Вейча нет необходимости, а аналитические выражения следуют из (2.16):
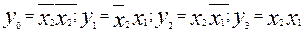
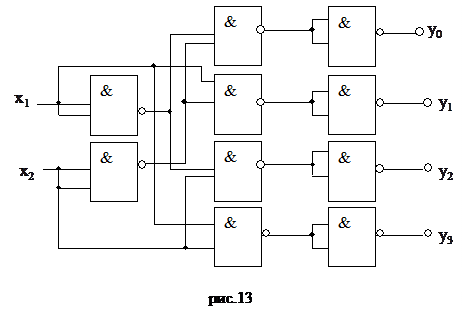
3.Исходя из этих выражений строим схему, например, в базисе «2И-НЕ» (рис.13).
Аналогичным способом строятся дешифраторы и на большее число входов.
 Преобразователь для семисегментного индикатора
Преобразователь для семисегментного индикатора
Семисегментный оптический индикатор представляет собой устройство, состоящее из семи светодиодов в виде отрезков прямой линии, которые принято обозначать буквами a, b, c, d, e, f, g расположенными таким образом, что свечение определенной их комбинации изображает определенную цифру (рис.14)
|
Например: для изображения цифры «0» необходимо, чтобы светились: a, b, c, d, e, f, т.е. на эти сегменты должны быть поданы уровни логической единицы (на сегмент g – уровень логического нуля). По способу изображения цифры N десятичной системы, заполняем таблицу функционирования (табл. 10).
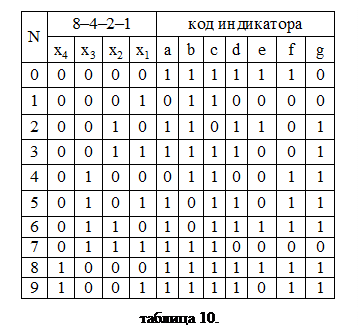 Учитывая, что с помощью 4-х разрядного входного кода можно отобразить десятичные числа от 0 до 15, в то время как одноразрядный семи сегментный индикатор способен отобразить числа только от 0 до 9, в диаграммах Вейча будет 6 избыточных комбинаций. Доопределяя их для каждой из семи выходных (a – g) функций можно получить минимальную ДНФ. Окончательные результаты из-за их громоздкости здесь не приводятся.
Учитывая, что с помощью 4-х разрядного входного кода можно отобразить десятичные числа от 0 до 15, в то время как одноразрядный семи сегментный индикатор способен отобразить числа только от 0 до 9, в диаграммах Вейча будет 6 избыточных комбинаций. Доопределяя их для каждой из семи выходных (a – g) функций можно получить минимальную ДНФ. Окончательные результаты из-за их громоздкости здесь не приводятся.
Мультиплексеры и демультиплесеры.
Особенности синтеза
2m – разрядным мультиплексером называется устройство, имеющее: m адресных входов, 2m- информационных, один выход и осуществляющее передачу двоичной информации на выход только с того информационного входа, десятичный номер которого совпадает с кодовой комбинацией в двоичном натуральном коде, установленной на адресных входах, независимо от состояния остальных информационных входов. Физически, мультиплексер можно интерпретировать многопозиционным (2m- входовым) переключателем (рис.15).
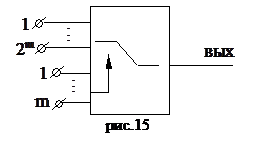 Рассмотрим синтез 4-х разрядного мультиплексера в базисе «2И-НЕ»:
Рассмотрим синтез 4-х разрядного мультиплексера в базисе «2И-НЕ»:
 1.Из определения следует, что в данном случае устройство имеет 4 информационных входа и 2 адресных и 1 вход. Обозначим информационные входы –
1.Из определения следует, что в данном случае устройство имеет 4 информационных входа и 2 адресных и 1 вход. Обозначим информационные входы – 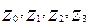 ; адресные -
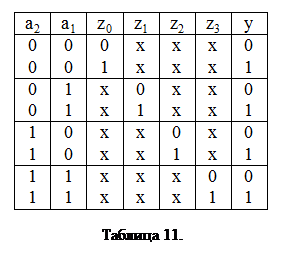
; адресные - 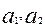 ; а выход - У, и составим таблицу функционирования (табл.11).
; а выход - У, и составим таблицу функционирования (табл.11).
Здесь (Х) – обозначает безразличное состояние переменной.
а). Каждому набору (из 4-х возможных) на адресных входах может соответствовать два возможных (0 или1) значения на соответствующем информационном входе, которые проходят на выход. Это нашло отражение в делении таблицы на четыре строки.
б). Кодовой комбинации на адресных входах 00 соответствует прохождение на выход сигнала с входа Z0(который практически имеет нулевой десятичный номер), кодовой комбинации 01 соответствует – вход Z1 и т.д. Причем, это проявляется независимо от состояния остальных информационных входов, следовательно, существуют безразличные состояния входных (а не выходных, ибо выходные переменные всегда определены) переменных. Другими словами, эти переменные в аналитическом выражении функции y (на каждом конкретном наборе) будут отсутствовать.
2. Составление диаграмм Вейча.
Общее количество формальных входных переменных равно 6 (4+2) и диаграмма Вейча становится очень громоздкой. Однако в данном случае составлять их нецелесообразно, т.к. сразу из табл.11 видно, что в ней отсутствуют смежные минтермы, следовательно, функция уже представляет собой ДНФ. По правилу перехода от табличного задания функции к аналитическому имеет:
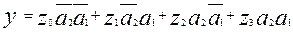 (2.21.1)
(2.21.1)
Переходя по т.Моргану к базису «И-НЕ» получаем схему(рис.16).
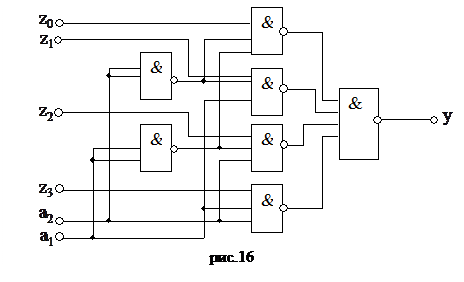
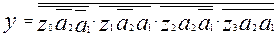 (2.21.2)
(2.21.2)
Окончательно перейти к базису «2И-НЕ», т.е. к использованию только двухвходовых элементов (как это требовалось в условии) можно с помощью тождества булевой алгебры.
Например: для трехвходового элемента «3И-НЕ» получим (рис.17)
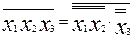
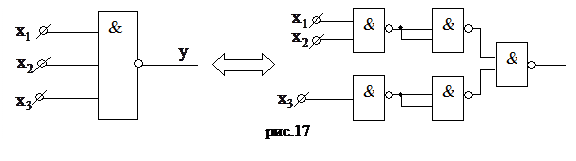
Для четврехвходового элемента «4И-НЕ» преобразование осуществляется аналогично, после чего необходимо внести эти изменения в рис.16 и получим окончательную схему, не приводимую по причине громоздкости.
Совершенно аналогично синтезируются мультиплексеры и на большее число разрядов.
2m – разрядным демультиплексером называется устройство, имеющее m – адресных входов, один информационный вход, и 2m – выходов, и осуществляющее передачу двоичной информации с информационного входа только на тот выход, десятичный номер которого совпадает с кодовой комбинацией в двоичном натуральном коде, установленной на адресных входах, при условии наличия логического «нуля» на остальных выходах.
Очевидно, демультиплексер выполняет функции обратные мультиплексеру. Рассмотрим синтез 4-х разрядного демультиплексера в базисе «И-НЕ».
1.  Из определения следует, что в данном случае устройство имеет 1 информационный вход, 2- адресных и 4 – выхода. Обозначим информационный вход – x, адресные входы –
Из определения следует, что в данном случае устройство имеет 1 информационный вход, 2- адресных и 4 – выхода. Обозначим информационный вход – x, адресные входы – 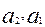 , выходы –
, выходы – 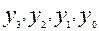 и составим таблицу функционирования (табл.11.1).
и составим таблицу функционирования (табл.11.1).
2. Составлять диаграмму Вейча и проводить минимизацию нет необходимости, т.к. выходные функции у0 ÷ у3 принимают единичное значение только на одном наборе входных переменных х, а1,а2. Следовательно можно сразу составить аналитические выражения:
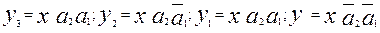 (2.21.3)
(2.21.3)
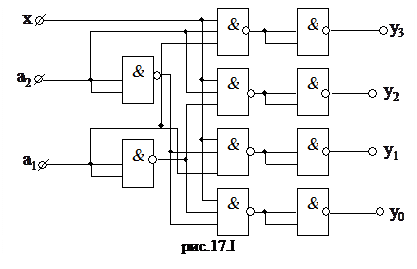
По которым изображаем схему (рис.17.1):
 Арифметические сумматоры.
Арифметические сумматоры.
Одноразрядный полный сумматор
Операция сложения двух одноразрядных чисел x1 и x2 и формирование результата суммы широко применяется в вычислительной технике, поскольку все остальные арифметические операции (умножение, деление, вычитание) можно выразить через операцию сложения чисел, представленных некоторыми специальными кодами. Результат сложения двух чисел дается выражением (2.6) при выполнении операции суммирования по модулю два (обозначается x1Å x2 или x1 mod 2x2). Исключение составляет случай сложения двух единиц, когда происходит переполнение, и для индикации этого приходится вводить новую переменную Р – сигнал переноса в старший разряд. В десятичной системе счисления аналогичная ситуация возникает когда складывают, например, 1+9=10, в данном случае разрядности единиц уже не хватает, и на единицу увеличивается разряд десятков. Отсюда следует, что при суммировании двух одноразрядных чисел, результат может быть числом двухразрядным, причем младший разряд определяется выражением (2.6), а старший равен Р. Ниже будет показано, что суммирование двух много разрядных чисел сводится к поразрядному суммированию, начиная с младшего разряда, с учетом переноса из предыдущего разряда.
Таким образом, одноразрядный полный сумматор, обеспечивает сложение трех двоичных цифр – слагаемых 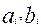 и сигнала переноса
и сигнала переноса 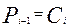 (из предыдущего младшего (i- 1) разряда). А на выходе формируется сумма этих трех цифр
(из предыдущего младшего (i- 1) разряда). А на выходе формируется сумма этих трех цифр 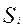 и сигнал переноса
и сигнал переноса 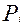 в старший
в старший
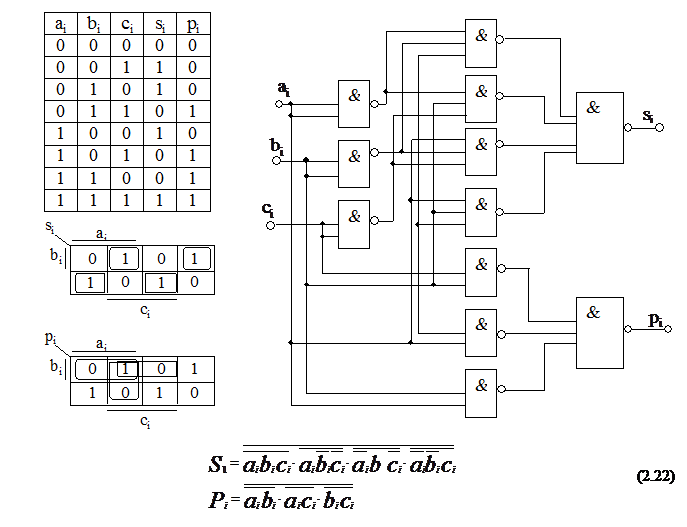
(i +1) разряд. Данные синтеза, по методике изложенной в п.2.7, одноразрядного полного сумматора в базисе «И-НЕ» приведены на рис.18.
Можно существенно упростить схему сумматора, если (2.22) переписать в виде:
 (2.23)
(2.23)
и воспользоваться двумя элементами «ИСКЛЮЧАЮЩЕЕ ИЛИ» (РИС.4.1.). Для доказательства (2.23) необходимо применить тождество (2.14.1).
Построение сумматоров двух многоразрядных чисел
Пусть 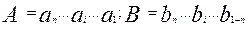 - разрядные двоичные числа и требуется найти их сумму
- разрядные двоичные числа и требуется найти их сумму 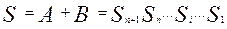 . Исходя из правил сложения двоичных чисел мы должны последовательно, начиная с младшего (1 – го) разряда, суммировать три цифры – цифры данного разряда слагаемых
. Исходя из правил сложения двоичных чисел мы должны последовательно, начиная с младшего (1 – го) разряда, суммировать три цифры – цифры данного разряда слагаемых 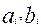 и сигнал переноса из предыдущего разряда.
и сигнал переноса из предыдущего разряда.
Например: А=13=1101, В= 11=1011 (в коде 8-4-2-1).
Тогда
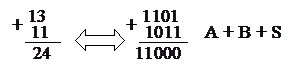 Здесь для изображения числа 24 понадобится дополнительный разряд, т.е. образно говоря, мы используем код «16-8-4-2-1».
Здесь для изображения числа 24 понадобится дополнительный разряд, т.е. образно говоря, мы используем код «16-8-4-2-1».
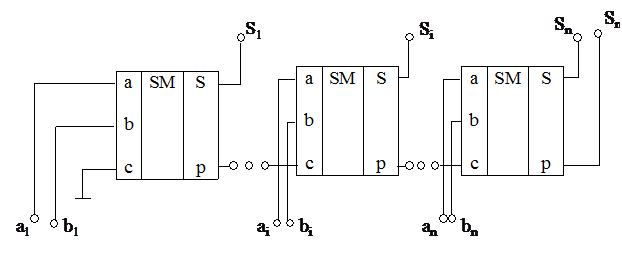
Следовательно сумматор двух многоразрядных чисел может быть построен путем соединения одноразрядных полных сумматоров по схеме(рис.19).
Условные обозначения входов одноразрядных сумматоров SM приведены в соответствие с рис. 18, т.е. число А подается на входы 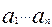 , число В – на входы
, число В – на входы 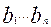 . В случае суммирования чисел А и В с несовпадающим числом разрядов, число с меньшим количеством разрядов дополняется нулями в старших разрядах, до разрядности другого числа.
. В случае суммирования чисел А и В с несовпадающим числом разрядов, число с меньшим количеством разрядов дополняется нулями в старших разрядах, до разрядности другого числа.
Цифровые компараторы
Цифровым компаратором (схемой сравнения) называется КЦА, осуществляющий сравнение двух или более n – разрядных двоичных чисел, представленных в одноименном коде, с определением знака неравенства.
Рассмотрим синтез схемы компаратора для сравнения двух n – разрядных чисел 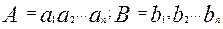 , представленных в коде «8-4-2-1», считая
, представленных в коде «8-4-2-1», считая 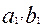 - старшими разрядами. В этом случае также можно пользоваться методом логического проектирования, изложенном в п.2.7, однако даже для 4-х разрядных чисел, общее число входных переменных равно восьми и таблица функционирования (не говоря о минимизации) становится весьма громоздкой. Поэтому воспользуемся методом эвристического проектирования, часто применяемым на практике, когда аналитическое выражение функции получают исходя из определения КЦА и логики его функционирования.
- старшими разрядами. В этом случае также можно пользоваться методом логического проектирования, изложенном в п.2.7, однако даже для 4-х разрядных чисел, общее число входных переменных равно восьми и таблица функционирования (не говоря о минимизации) становится весьма громоздкой. Поэтому воспользуемся методом эвристического проектирования, часто применяемым на практике, когда аналитическое выражение функции получают исходя из определения КЦА и логики его функционирования.
Учитывая однозначность кода «8-4-2-1» сравнение можно производить поразрядно, следующим образом. Компаратор должен одновременно реализовать три логические функции:
функция равенства (равнозначности) чисел А и В
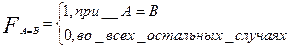 (2.24)
(2.24)
функция, отражающая превышение числа А над числом В
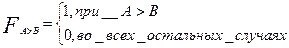 (2.25)
(2.25)
функция, отражающая превышение числа В над числом А
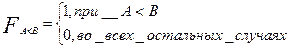 (2.26)
(2.26)
Получим аналитическое выражение для функции равенства (равнозначности) двух чисел А и В. Очевидно, А будет равно В только если равны все их соответствующие разряды (т.е. 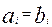 для
для 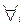 ).
).
Следовательно, из (2.24) следует:
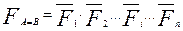 , где (2.27)
, где (2.27)
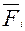 -функция равнозначности I – го разряда, полученная инвертированием функции неравнозначности (см. 2.14.1):
-функция равнозначности I – го разряда, полученная инвертированием функции неравнозначности (см. 2.14.1):
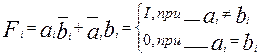 (2.28)
(2.28)
Определение знака соотношения чисел А и В, в случае А > В, осуществляется путем последовательного сравнения их одноименных разрядов. В начале сравниваются коды в первом (старшем) разряде, если 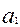 >
> 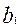 , а это возможно только при
, а это возможно только при 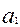 =1,
=1, 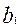 =0, можно сразу сделать вывод, что, А>В независимо от соотношения остальных разрядов.
=0, можно сразу сделать вывод, что, А>В независимо от соотношения остальных разрядов.
Аналитически это можно записать в виде некоторой функции 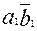 , которая равна 1 только при
, которая равна 1 только при 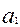 =1,
=1, 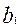 =0, и равна нулю во всех остальных случаях.
=0, и равна нулю во всех остальных случаях.
Следовательно, функцию 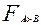 можно искать в виде:
можно искать в виде:
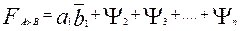 (2.29)
(2.29)
где 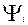 – функция, определяющая соотношение между I-ми разрядами, при условии равенства всех предыдущих.
– функция, определяющая соотношение между I-ми разрядами, при условии равенства всех предыдущих.
Если же старшие разряды чисел А и В совпадают, то следует проанализировать соотношение кодов во втором разряде. Если совпадают цифры и во втором разряде, необходимо проанализировать третий разряд и т.д. Следовательно, из (2.25) и (2.29) можно записать:
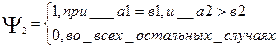 (2.30)
(2.30)
Учитывая, что Y2 =Y2 (а1 , в1, а 2, в 2) зададим ее таблично и минимизируем по Вейчу (рис. 20).
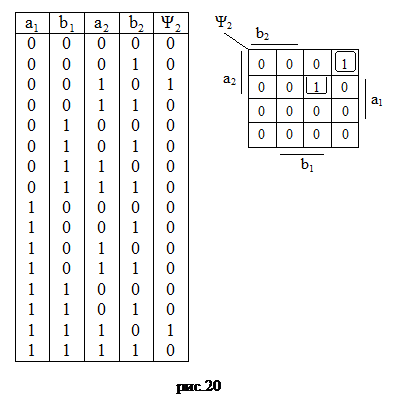 |
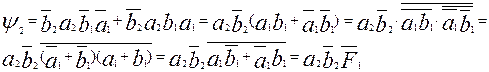
где 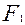 - функция неравнозначности 1-го разряда. Аналогично можно показать:
- функция неравнозначности 1-го разряда. Аналогично можно показать:
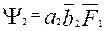 ;
;
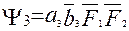 ; (2.31)
; (2.31)
……………………
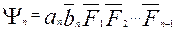 ;
;
где 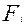 - функция неравнозначности i-го разряда. Таким образом, окончательно получим из (2.29) – (2.31):
- функция неравнозначности i-го разряда. Таким образом, окончательно получим из (2.29) – (2.31):
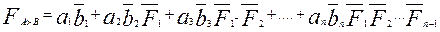 ; (2.32)
; (2.32)
Проводя подобные рассуждения для 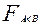 , можно найти ее аналитическое выражение. Условие требуемого (А < В) неравенства для первого разряда, имеет вид
, можно найти ее аналитическое выражение. Условие требуемого (А < В) неравенства для первого разряда, имеет вид 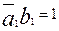 .
.
Тогда:
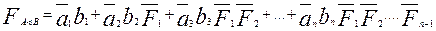 (2.33)
(2.33)
Можно показать, что выражения 92.27, 2.32, 2.33) не содержат смежных минтермов, следовательно, полученные выражения являются минимальным ДНФ.
Пример: синтезировать схему двухразрядного компаратора в базисе «И – НЕ». Из (2.27, 2.32, 2.33) для n=2 получим:

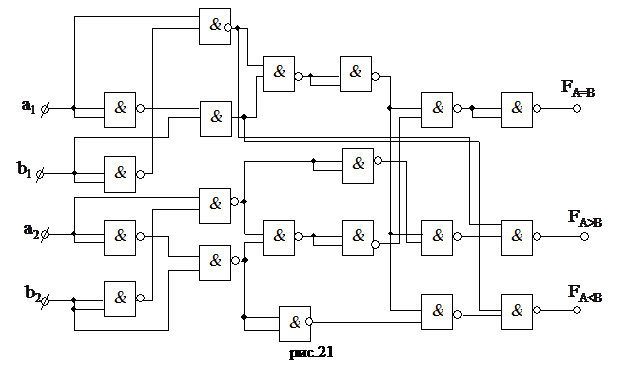
Переводя по т. Моргана в базис «И – НЕ», получим схему (рис.21).
На практике часто применяются так называемые двухпороговые компараторы, определяющие попадает ли данное число В в требуемый интервал, т.е. решающее неравенство А£ В£ С.
Имея два однопороговых компаратора, эту задачу легко решить, представив функцию 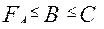 в виде:
в виде:
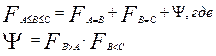 (2.34)
(2.34)
Обозначение и физический смысл функции аналогичны приведенным на рис.21.
1.9. НЕКОТОРЫЕ КЦА, ВХОДЯЩИЕ В
СОСТАВ ТТЛ СЕРИЙ
Все рассмотренные в п. 2.8 КЦА широко представлены в составе ТТЛ серий интегральных микросхем. Никаких принципиальных отличий синтезированных нами структур от их интегральных аналогов не имеется. В ряде микросхем мультиплексеров типа К155КП1,5,7, дешифраторов К155ИД1, 3, 7 дополнительно предусмотрены лишь входы разрешения, блокировки и выдача данных в прямом и инверсном виде.
 Рассмотрим некоторые из микросхем, находящие широкое применение при построении микропроцессорных и вычислительных устройств.
Рассмотрим некоторые из микросхем, находящие широкое применение при построении микропроцессорных и вычислительных устройств.
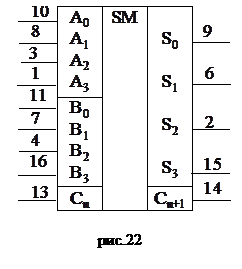
Микросхема К155ИМ3 – полный четырехразрядный сумматор (рис.22), цифры около выводов соответствуют номерам «ножек» микросхемы, позволяющий складывать два четырехразрядных числа: 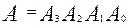 , и
, и 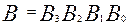 (разряды расположены в порядке убывания) и формирующий на выходе результат
(разряды расположены в порядке убывания) и формирующий на выходе результат 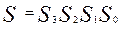 и сигнала переноса в следующий разряд -
и сигнала переноса в следующий разряд - 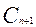 .
.
Структурно микросхема К155ИМ3 построена в соответствии с рис.19, а выход переноса из предыдущего разряда 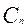 соответствует входу C первого разряда на рис.19.
соответствует входу C первого разряда на рис.19.
На практике эта микросхема используется для построения сумматоров двух 8-разрядных чисел 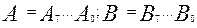 (их называют словами или байтами), путем каскадного соединения двух м/с К155ИМ3.
(их называют словами или байтами), путем каскадного соединения двух м/с К155ИМ3.
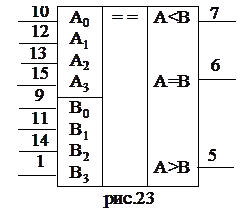
Микросхема К155СП1 – 4-х разрядный цифровой компаратор (рис.23), позволяет сравнивать два 4-х разрядных числа, 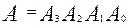 и
и 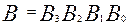 (указаны в порядке убывания разрядов) и формировать признак соотношения между ними в виде уровня логической единицы на одном из выходов: А=В, А<В, А>В. Структурно микросхема К155СП1 построена в соответствии с выражениями (2.27, 2.32, 2.33), а обозначения и логика работы совпадают с приведенными в подпункте «ЦИФРОВЫЕ КОМПАРАТОРЫ».
(указаны в порядке убывания разрядов) и формировать признак соотношения между ними в виде уровня логической единицы на одном из выходов: А=В, А<В, А>В. Структурно микросхема К155СП1 построена в соответствии с выражениями (2.27, 2.32, 2.33), а обозначения и логика работы совпадают с приведенными в подпункте «ЦИФРОВЫЕ КОМПАРАТОРЫ».
1. Алесенко А.Г., Шагурин И.И. Микросхемотехника. - М., Радио и связь, 1982г.
2. Алексенко А.Г. Основы микросхемотехники. - М., Советское радио, 1977г.
3. Букреев И.Н., Мансуров Б.М., Горячев В.И., Микроэлектронные схемы цифровых устройств. – М., Советское радио, 1975
4. Гаврилов М.А., Девятков В.В., Пупырев Е.И.- Логическое проектирование дискретных автоматов. - М., Наука, 1977г.
 2015-02-14
2015-02-14 5449
5449
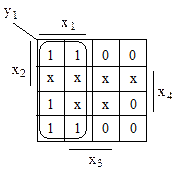
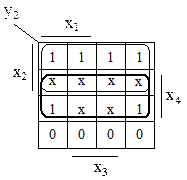
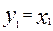
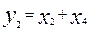
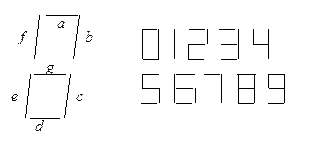 рис.14
рис.14 






