Пуассоновский процесс

Сначала рассмотрим пуассоновский процесс, который является потоком событий простейшего типа и, кроме того, сам играет важную роль во многих приложениях. Например, пуассоновский процесс служит моделью для потоков таких событий, как радиоактивные распады, телефонные вызовы или обращения в страховое общество. Разумеется, в некоторых случаях эта модель дает хорошее приближение к истинной ситуации, а иногда используется лишь на начальном этапе изучения явлений.

Построим пуассоновскую модель на основании следующих предложений Хинчина [5]:

1. Вероятность Р_n (t) того, что в интервале времени длительностью t произойдет ровно n событий, зависит от n и t, но не зависит от положения этого интервала на временной оси (условие стационарности).

2. Числа событий, происшедших в течение непересекающихся интервалов времени, являются независимыми случайными величинами (отсутствие последствия).

3. Вероятность того, что в малом интервале времени длительностью t произойдет более одного события, есть величина порядка меньше t, т.е. при t ®0 эта вероятность равна 0(t) (условие ординарности).

Рассмотрим следствия, вытекающие из условий 1 – 3.

Из условий 1 и 2 вытекает, что для любых t и u

Р ₀(t + u) = P ₀(t) P ₀(u).

Единственным решением этого уравнения, для которого 0 < P ₀(t) £ 1, является

,

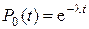где l – некоторая неотрицательная константа. Исключая тривиальный случай Р₀(t)=1 для всех t, можно считать l > 0. (Другие тривиальные решения P ₀(t)=0 не совместимо с условиями 2 и 3.) Для малых t

P ₀(t) = 1– l t + 0(t),

и из условия 3 получаем

Р ₁(t) = 1 – Р ₀(t) + 0(t) = l t + 0(t).

Далее в силу условий 2 и 3 для n ³1

Р_n (t + t) = (1 – lt) P_n (t) + lt P_{n -1}(t) + 0(t).

Поделив обе части на t и устремив t к нулю, убеждаемся, что производная Р_n ¹(t) существует и удовлетворяет соотношению

Р_n ¹(t) = l[ P_{n –1}(t) – P_n (t)]. (1.2)

Положив Р_n (t) = 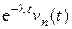, получим .

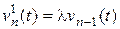Единственным решением этой системы, удовлетворяющим условиям v ₀(0) = 1, v_n (0) = 0 для всех n ³ 1, является

.

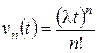Следовательно, единственным решением системы (1.2), при условии Р_n (0) = 0 для всех n ³ 1 и P ₀(0) = 1, будет

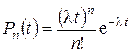. (1.3)

Определим теперь случайный процесс x(t), который даст возможность описать вероятностную структуру пуассоновского процесса. Пусть x(t) обозначает число пуассоновских событий на интервале времени (0, 1]; приращение x(t + u) – x(u) есть число событий на интервале (u, u + t ]. Тогда x(t), так же как и любое приращение x(t + u) – x(u), будет иметь пуассоновское распределение с параметром l t.

Определим конечномерные распределения x(t) соотношением

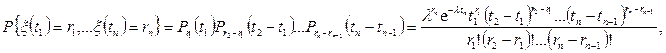
где r ₁ £ r ₂ £ … £ r_n – целые числа; t ₁ < t ₂ < … < t_n. Ясно, что условия 1–3 и условия согласованности теоремы Колмогорова выполняются. Следовательно, существует вероятностная мера на функциональном пространстве Х, которая определяется этими конечномерными распределениями.

Построим эквивалентный вариант x(t) следующим образом. Из вида конечномерных распределений следует, что с вероятностью единица x(t) не убывает на множестве всех рациональных t; оставим без изменения x(t) для всех рациональных t, а для иррациональных t положим x(t) = 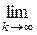x(t_k), где t_k – рациональны и меньше t. Нетрудно видеть, что так определяемый процесс эквивалентен x(t), поскольку значения нового процесса являются с вероятностью единица пределами величин x(t_k), а x(t) – предел по вероятности этих величин, что следует из специфики конечномерных распределений.

Далее с вероятностью единица этот эквивалентный вариант x(t) не убывает и в каждом конечном интервале имеет не более конечного числа единичных скачков. Эти скачки соответствуют появлениям пуассоновских событий, и мы можем определить, например, случайные величины m₁, m₂, …, m _n где m _n – промежуток времени между появлениями (n – 1) и n -го событий после момента t = 0.

Последнее замечание приводит к другому естественному способу определения процесса x(t) с помощью параметрического метода (второй способ § 1.5). Рассмотрим множество Х ₀ всех функций x(t), определенных для t ³ 0 соотношениями

x(t) = 0 при 0 £ t < m_1,

x(t) = n при m₁ + … + m _n £ t < m₁ + … + m _{n +1},

где m₁, m₂, … – положительные параметры. Множество Х ₀ является подмножеством функционального пространства Х и каждое x(t) Î X ₀ будет ступенчатой функцией, имеющей единичные скачки в точках t = m₁ + … + + m _n. Пусть параметры m _j являются независимыми случайными величинами с плотностью распределения le^{-l t}. Тогда сумма m₁ + … + m _n имеет плотность (l ⁿtⁿ / n!)e^{-l t}, и легко заметить, что совместное распределение случайных величин x(t ₁), …, x(t_k) совпадает с введенным ранее распределением для процесса Пуассона (1.3).