2015-02-14
505
На практике часто сталкиваются со случаем, когда наблюдения за случайно меняющейся системой производятся через равные промежутки времени. Взяв в качестве единицы времени промежуток между двумя последовательными измерениями, получим последовательность случайных величин, т.е. случайный процесс с целочисленным параметром.
Изменим прежние обозначения: параметр будем обозначать n вместо t, а случайную величину, наблюдаемую в момент n, будем обозначать x n или x n (w) вместо x(t, w). Множество Т значений параметра будет состоять из всех рассматриваемых n; чаще всего Т будет множеством всех целых чисел n =..., -1, 0, 1,... или множеством всех положительных чисел n 1 = = 1, 2,...
Последовательность случайных величин x n = x n (w), n = 1, 2,..., переводит каждую фиксированную точку w основного вероятностного пространства в некоторую точку x = (x1, x2,...) бесконечномерного пространства R ¥. Иными словами, выборочным пространством Х является пространство R ¥, состоящее из всех точек х = (х 1, х 2,...) с бесконечным числом координат. Интервал в R ¥ представляет собой множество точек х, удовлетворяющих конечному числу неравенств вида aj < xj < bj с теми же замечаниями о знаках неравенств, что и в общем случае (§ 1.3).
|
|
|
Предположим, что дана последовательность случайных величин x n = = x n (w), n = 1, 2,.... Тогда любое конечное множество величин x n, например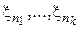 
, имеет совместное распределение вероятностей с функцией распределения
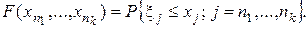
В силу первой части теоремы Колмогорова семейство всех функций F однозначно определяет вероятность того, что точка x = (x1,...) принадлежит множеству В < R¥ для любого борелевского В.
Пусть теперь дано лишь семейство { F } функций распределения F (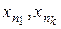
) с любыми k и ni, удовлетворяющее условиям симметрии и согласованности. Вторая часть теоремы Колмогорова показывает, что это семейство однозначно определяет распределение вероятностей в классе борелевских множеств в R ¥.
Таким образом, в обоих случаях в R ¥ может быть построено некоторое распределение вероятностей, соответствующее бесконечной случайной последовательности x = (x1, x2,...). Вероятность того, что эта последовательность как точка в R ¥ будет принадлежать данному множеству А, однозначно определяется для любого борелевского А в R ¥.
Оказывается, что все множества в R ¥, которые могут быть определены с помощью обычных аналитических операций над x n, являются борелевскими. Это очень важный факт; он означает, что в случае дискретных последовательностей случайных величин все события, с которыми сталкиваются, имеют вполне определенные вероятности. В непрерывном случае ситуация далеко не так проста.
Пример 1.1. Рассмотрим три простых примера борелевских множеств в R ¥, определенных с помощью простых операций над последовательностью случайных величин x1, x2,... Каждый из этих примеров существенен для различных приложений.
|
|
|
Пусть h – некоторое число. Обозначим А, В и С множества в R ¥, определенные следующими соотношениями:
А: supx n £ h,
В: limx n = h,
С: limx n – существует и конечен,
где n пробегает множество положительных чисел. Покажем, что каждое из этих множеств может быть получено из интервалов в R ¥ с помощью счетного числа операций, так что все они являются борелевскими. Для любых положительных целых чисел m, n и q обозначим через In, Kn,q и Lm,n,q, интервалы в R ¥, определенные неравенствами:
In: x n £ h,
Kn,q: ú x n – h ú <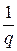 
,
Lm,n,q: ú x m – x n ú < .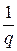
Множества А, В и С могут быть построены из этих интервалов с помощью пересечений и объединений следующим образом:
,
,
.
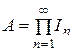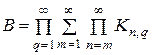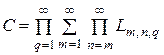Отсюда следует, что множества А, В, С являются борелевскими.
