Примеры случайных процессов

Приведем примеры случайных процессов, которые можно определить и изучить на основе понятий, введенных ранее в этой главе.

Пример 1. 5. Процесс с взаимно независимыми значениями. Пусть F_n (Х) – последовательность одномерных функций распределения, где n пробегает множество целых чисел. Для любой конечной группы целых чисел n ₁, …, n_k функция

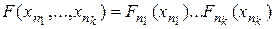
является k -мерной функцией распределения. Очевидно, что семейство всех таких F с k = 1,2, … удовлетворяет условиям симметрии и согласованности. Следовательно, по теореме Колмогорова существует случайный процесс с целочисленным параметром …, x_–1, x₀,x₁, …, семейство конечномерных распределений которого совпадает с семейством всех F. В силу определения F, случайные величины x _n взаимно независимы. Процесс x _n называется процессом с взаимно независимыми значениями.

Пример 1.6. Стационарный марковский процесс. Пусть x₁, x₂, … – последовательность независимых случайных величин, распределенных нормально с параметрами (0, 1); иначе говоря, каждая случайная величина x _n имеет нормальную функцию распределения j(x). Определим новую последовательность случайных величин:

h₁ = x₁,

h₂ = r x₁ + (1 – r ²)^1/2 x₂,

h _n = r^{n- 1} x ₁ + (1 – r ²)^1/2 (r^{n -2} x ₂ + r^{n -3} x ₃ + … +x _n),

где r – некоторое число, ½ r ½< 1. Для всех m и n

Sh _n = 0, Sh _n ² = 1, Sh _m h _n = r ^{½ m – n ½}.

Любая конечная группа величин h _n имеет совместное нормальное распределение с нулевыми средними, единичными дисперсиями и с коэффициентами корреляции для любой пары h _n и h _т, равными r ^{½ m-n ½}, так что свойство стационарности имеет здесь место.

Найдем

h = x₁,

,

.

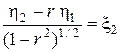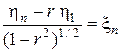Случайные величины, стоящие в этих равенствах справа, независимы и нормально распределены с параметрами (0, 1). Следовательно, условная плотность распределения

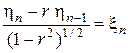
при условии, что величины x₁, …, x _{n –1} приняли некоторые определенные значения, не зависит от этих значений и равна нормальной плотности j(x). Величины x₁, …, x _{n –1} однозначно определяют h₁, …, h _{n –1}, и наоборот. Поэтому условное распределение h _{n –1} при данных h₁, …, h _{n –1} нормально с условным средним r h _{n –1} и дисперсией (1 – r ²)^1/2. Заметим, что это распределение зависит только от непосредственно предшествующей величины h _{n –1} и не зависит от h₁, …, h _{n –2}. Случайный процесс, для которого зависимость от прошлого носит такой характер, называется марковским.

Приведенные примеры иллюстрируют применение теоремы Колмогорова при доказательстве существования случайных процессов с конечномерными распределениями.