Лабораторная работа № 8. Методы одномерной оптимизации

Задание: Найти положение точки экстремума и экстремальные значения целевой функции f(x) на интервале [a, b] методом золотого сечения. Длина конечного интервала неопределенности не должна превышать 0,0001.

Номер варианта	Вид целевой функции f(x)	a	b	Экстремум
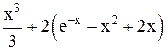
				Max
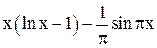
		0,5	1,5	Min
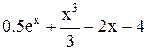
				Min
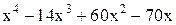
				Min
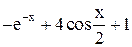
				Max
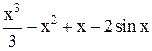
				Min
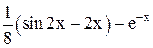
		0,5	1,5	Max
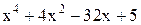
				Min
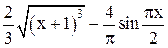
				Min
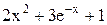
				Min
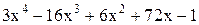
		-1,4	-0,4	Min
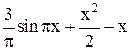
				Max
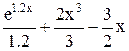
				Min
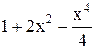
		-2,8	-1,8	Max
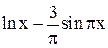
				Max
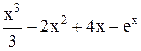
				Max
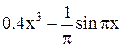
				Min
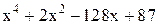
		2,5	3,5	Min
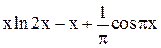
		0,5	1,5	Min
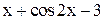
				Max
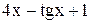
		0,2	1,2	Max
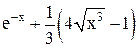
				Min
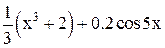
		0,2	1,2	Min
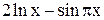
				Max
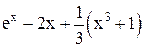
				Min
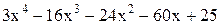
		4,8	5,8	Min
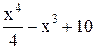
		2,3	3,3	Min
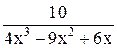
		0,2	1,2	Max
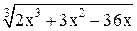
		1,7	2,7	Min
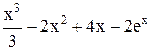
				Max
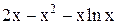
		0,1	1,1	Max
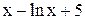
		0,3	1,3	Min
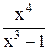
		1,1	2,1	Min
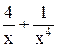
		-1,4	-0,4	Min
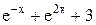
		-1		Min
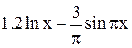
				Min
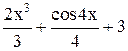
				Min
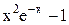
		1,4	2,4	Max
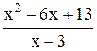
		4,6	5,6	Min
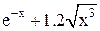
				Min
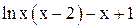
				Min
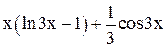
		0,5	1,5	Min
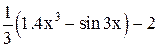
				Min
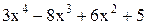
		-0,4	0,6	Min
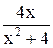
		1,6	2,6	Max
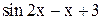
				Max
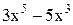
		0,5	1,5	Min
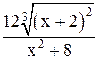
		-2,4	-1,4	Min
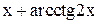
				Min
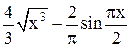
				Min

Вопросы для самоподготовки

1. Что такое оптимизация?

2. Что понимается под количественной оценкой оптимизируемого качества?

3. Какие типы задач оптимизации существуют?

4. В чем состоит безусловная задача оптимизации?

5. В чем состоит условная задача оптимизации?

6. В каком случае используется одномерная оптимизация?

7. В чем состоит основная задача одномерной оптимизации?

8. Дайте сравнительную характеристику методов одномерной оптимизации.

9. Метод сканирования.

10. Метод локализации.

11. Метод золотого сечения.

12. Метод поиска с использованием чисел Фибоначчи.