Точка, отстоящая от оси вращения на расстоянии R, при повороте на угол φ проходит путь (рис. 14):
s = Rφ (23)
Продифференцируем это выражение по времени:
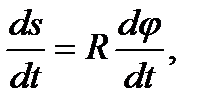
или
v = Rω. (24)
Полученная формула выражает линейную скорость точки, движущейся по окружности с постоянной угловой скоростью ω. Продифференцируем уравнение (24):
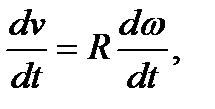
или
aτ = Rε. (25)
Формула (25) связывает тангенциальное и угловое ускорения точки. Выражение для нормального ускорения было получено ранее (17).
Векторы угловой скорости, линейной скорости и радиус-вектор точки связаны векторным произведением:
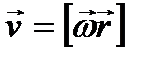 . (26)
. (26)
При этом векторы 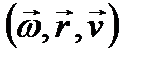 образуют правую тройку: если вращать буравчик от вектора
образуют правую тройку: если вращать буравчик от вектора 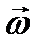 к вектору
к вектору 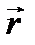 по кратчайшему направлению, то он будет двигаться вдоль направления
по кратчайшему направлению, то он будет двигаться вдоль направления 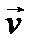 .
.
 2015-02-14
2015-02-14 1412
1412








