устанавливает связь между подвижностью m носителей заряда е и их коэф. диффузии D: 
Э. <с. написано в 1905 при построении теории броуновского движения А. Эйнштейном и M. Смолуховским(M. Smoluchowski). Ур-ние движения для частицы массы /и имеет вид
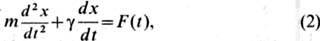 где g - коэф. трения, F(t)- случайная сила. Помножив (2) на.Y и усреднив по частицам, учитывая, что
где g - коэф. трения, F(t)- случайная сила. Помножив (2) на.Y и усреднив по частицам, учитывая, что 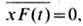 а
а 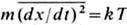 ' (принцип равногораспределения энергии по всем степеням свободы), получаем ур-ние
' (принцип равногораспределения энергии по всем степеням свободы), получаем ур-ние 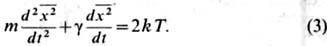
Интегрируя ур-ние (3) дважды, при 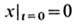 находим, что при
находим, что при 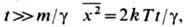 и, сравнивая сопределением коэф. диффузии
и, сравнивая сопределением коэф. диффузии 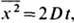 приходим к выражению D =
приходим к выражению D = 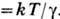 Учитывая, что
Учитывая, что 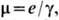 получаем (1). Э. <с. справедливо для классич. систем, находящихся в термодинамич. равновесии. Дляквантовых систем взаимодействующих частиц вместо (1) следует написать
получаем (1). Э. <с. справедливо для классич. систем, находящихся в термодинамич. равновесии. Дляквантовых систем взаимодействующих частиц вместо (1) следует написать  где
где 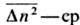 . флуктуация плотности числа частиц, а
. флуктуация плотности числа частиц, а 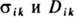 -симметричные компоненты тензоров проводимости и коэф. диффузии. Э. с. являетсяисторически первым примером флуктуационно-диссипативного соотношения
-симметричные компоненты тензоров проводимости и коэф. диффузии. Э. с. являетсяисторически первым примером флуктуационно-диссипативного соотношения
29. Уравнение непрерывности (вывод).
Представим себе, в некоторой проводящей среде, где течет ток, замкнутую поверхность S. Для замкнутых поверхностей векторы нормалей, а следовательно, и векторы 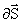 принято брать наружу, поэтому интеграл
принято брать наружу, поэтому интеграл 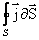 дает заряд, выходящий в единицу времени наружу из объема V, охваченного поверхностью S. Мы знаем, что плотность постоянного электрического тока одинакова по всему поперечному сечению S однородного проводника. Поэтому для постоянного тока в однородном проводнике с поперечным сечением S сила тока:
дает заряд, выходящий в единицу времени наружу из объема V, охваченного поверхностью S. Мы знаем, что плотность постоянного электрического тока одинакова по всему поперечному сечению S однородного проводника. Поэтому для постоянного тока в однородном проводнике с поперечным сечением S сила тока:
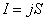 | (7.3.1) |
Из (7.3.1) и постоянства значения I во всех участках цепи постоянного тока следует, что плотности постоянного тока в различных поперечных сечениях 1 и 2 цепи обратно пропорциональны площадям 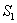 и
и 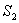 этих сечений (рис. 7.2):
этих сечений (рис. 7.2):
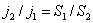 . . | (7.3.2) |
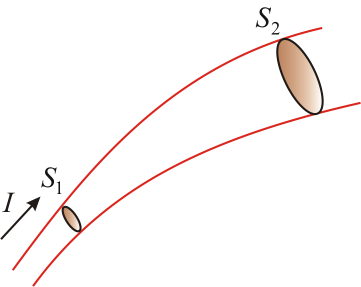
Рис. 7.2
Пусть S – замкнутая поверхность, а векторы 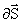 всюду проведены по внешним нормалям
всюду проведены по внешним нормалям 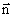 . Тогда поток вектора
. Тогда поток вектора 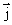 сквозь эту поверхность S равен электрическому току I, идущему вовне из области, ограниченный замкнутой поверхностью S. Следовательно, согласно закону сохранения электрического заряда, суммарный электрический заряд q, охватываемый поверхностью S, изменяется за время
сквозь эту поверхность S равен электрическому току I, идущему вовне из области, ограниченный замкнутой поверхностью S. Следовательно, согласно закону сохранения электрического заряда, суммарный электрический заряд q, охватываемый поверхностью S, изменяется за время 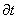 на
на 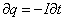 , тогда в интегральной форме можно записать:
, тогда в интегральной форме можно записать:
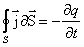 . . | (7.3.3) |
Это соотношение называется уравнением непрерывности. Оно является, по существу, выражением закона сохранения электрического заряда.
Дифференциальная форма записи уравнения непрерывности записывается так:
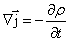 или или 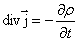 | (7.3.4) |
В случае постоянного тока, распределение зарядов в пространстве должно оставаться неизменным:
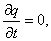
следовательно,
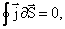 | (7.3.5) |
это уравнение непрерывности для постоянного тока (в интегральной форме).
Линии 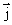 в этом случае нигде не начинаются и нигде не заканчиваются. Поле вектора
в этом случае нигде не начинаются и нигде не заканчиваются. Поле вектора 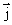 не имеет источника. В дифференциальной форме уравнение непрерывности для постоянного тока
не имеет источника. В дифференциальной форме уравнение непрерывности для постоянного тока 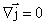 .
.
Если ток постоянный, то избыточный заряд внутри однородного проводника всюду равен нулю. В самом деле, т.к. для постоянного тока справедливо уравнение 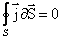 , то
, то
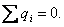
Избыточный заряд может появиться только на поверхности проводника в местах соприкосновения с другими проводниками, а также там, где проводник имеет неоднородности.
 2015-02-15
2015-02-15 1525
1525








