Для нахождения экстремумов функций многих переменных существует две альтернативные возможности.
Первая заключается в использовании блока given и функции minerr.
Определим функцию двух переменных
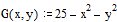
Зададимся целью найти ее экстремум в области x=[–5,5] y=[–5,5]. Оценим по графику положение экстремума.
Заносим в матрицу М значения функции в узловых точках
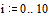
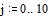
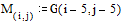

На заданном интервале функция не превосходит 25. Зададим начальные приближения для поиска экстремума
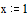
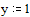
Записываем блок уравнений или неравенств. Число уравнений и неравенств в блоке given – Find должно быть больше и равно числа искомых величин. Если уравнений и неравенств не хватает, то можно просто продублировать одно и то же уравнение или вписать какое–либо тождество, например, 2=2.

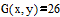
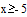
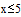
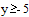
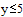
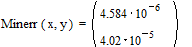
Функция Minerr ищет приближенной решение для системы уравнений и неравенств, записанных в блоке. В данном случае мы получили, что системе уравнений наилучшим образом соответствует точка [0,0]. (Поскольку по умолчанию точность вычислений составляет 0.001, мы округлили результат до 0).
Из графика видно, что значение 26 больше самого большого значения функции в окрестностях точки [1,1], то есть точное решение найти нельзя и функция Minerr подбирает такое значение x, при котором функция ближе всего к значению 26.
Вторая возможность – поиск нулей первой производной, то есть стандартный математический подход. Для этого можно использовать блок given – Find. Функция Find ищет точное решение системы уравнений и неравенств, записанных после слова given.

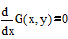
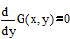
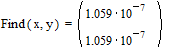
Результаты, полученные различными методами, совпадают, врем счета мало в обоих случаях.
В старших версиях Mathcad’а появилась дополнительная возможность поиска экстремумов с помощью функций Minimize и Maximize, которые могут быть использованы как сами по себе, так и совместно с блоком given. Аргументы функций: имя функции, экстремум которой ищется, и список ее аргументов.
Определяем функцию двух переменных 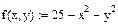 и задаем начальные приближения
и задаем начальные приближения 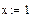
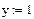 .
.
Задаем область поиска максимума внутри блока given
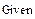
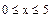
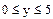
Находим максимум функции в заданной области
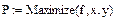
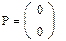
В случае функции одной переменной задаем функцию 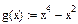 и начальное приближение
и начальное приближение 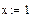
Находим максимум 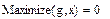
Если мы хотим найти максимальное или минимальное значение функции на некотором интервале, то необходимо определить этот интервал в блоке given
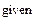
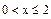
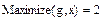
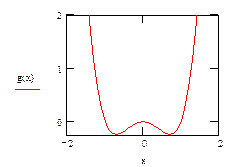
На приведенном ниже графике видно, что первый из найденных максимумов соответствовал случаю, когда производная обращается в ноль; второй максимум лежит на границе интервала.
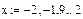
 2015-02-15
2015-02-15 579
579








