Решим еще раз задачу Коши для дифференциального уравнения первого порядка 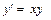 методом Рунге–Кутты.
методом Рунге–Кутты.
Зададим границы изменения x: 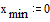
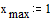
Зададим число точек внутри интервала 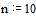
Зададим начальные условия 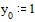
Обратите внимание на обозначения! Поскольку мы решаем только одно дифференциальное уравнение первого порядка, а не систему дифференциальных уравнений, матрица y содержит только один элемент, однако запись y=1 была бы неправильной. Необходимо явно указывать на то, что величина y – матрица, то есть писать индекс.
Определим теперь матрицу производных. Эта матрица тоже состоит только из одного элемента. Этот элемент с точностью до обозначений совпадает с правой частью исходного дифференциального уравнения: 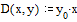
Решаем дифференциальное уравнение 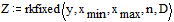
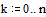
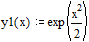
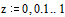
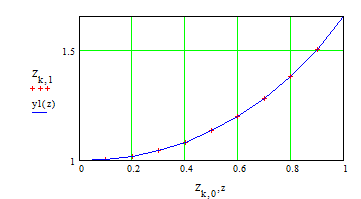
Точное аналитическое решение и решение, полученное численно отличаются в точке 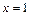 на
на 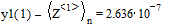
Относительная ошибка составляет 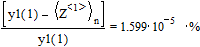
 2015-02-15
2015-02-15 289
289








