Пусть требуется найти решение дифференциального уравнения 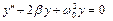 при условиях
при условиях 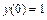 и
и 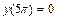 .
.
При значениях параметров 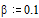
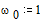
Для решения краевой задачи имеется встроенная функция sbval, реализующая метод стрельб и позволяющая свести краевую задачу к задаче Коши. Функция sbval имеет следующие параметры:
· v – вектор, содержащий начальные приближения для недостающих начальных условий,
· xmin, xmax – границы интервала, на котором ищется решение,
· D(x,y) – вектор–функция, содержащий правые части системы дифференциальных уравнений первого порядка, эквивалентной исходному уравнению, размер вектора n совпадает со степенью старшей производной дифференциального уравнения
· load(xmin,v) – вектор–функция, элементы которой соответствуют n значениям функций на левой границе интервала. Часть этих значений известна, а для части заданы начальные приближения в векторе v. Их уточненные значения будут найдены в процессе вычисления
· score(xmax,y) – вектор–функция, имеющая то же число элементов, что и v. Каждое значение является разностью между начальными значениями в конечной точке интервала и соответствующей оценки для решения. Этот вектор показывает, на сколько близко найденное решение к истинному.
|
|
|
Наша задача сводится к системе двух дифференциальных уравнений первого порядка:
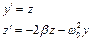
Поэтому функция D имеет вид 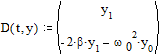
Задаем граничные условия: 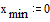
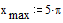
Задача Коши для дифференциального уравнения второго порядка содержит два начальных условия. Нам известно только одно. Начальное приближение для недостающего значения задаем в векторе v, который в нашем случае состоит только из одного элемента. Несмотря на это, индекс о должен быть обязательно указан, чтобы подчеркнуть векторный характер этой величины: 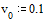
На левой границе интервала нам известно значение 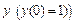 и задано начальное приближение для
и задано начальное приближение для 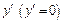 . Это значение записано в
. Это значение записано в 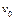 . Задаем вектор-функцию load. Ее нулевой элемент – начальное значение для
. Задаем вектор-функцию load. Ее нулевой элемент – начальное значение для 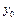 , первый – для
, первый – для 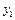 .
.
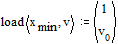
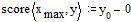
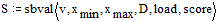
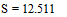
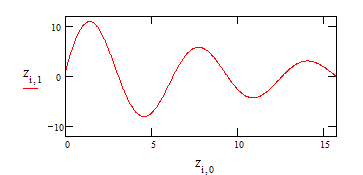
Теперь, когда нам стало известно недостающее начальное условие в задаче Коши, можно воспользоваться, например, функцией rkfixed
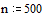
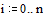
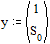
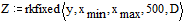
 2015-02-15
2015-02-15 445
445








