Для решения уравнений Пуассона 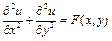 и Лапласа (частный случай, когда
и Лапласа (частный случай, когда 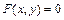 ) – уравнений эллиптического типа – предназначена функция relax(a, b, c, d, e, f, u, rjac), реализующая метод релаксации. Фактически, эту функцию можно использовать для решения эллиптического уравнения общего вида
) – уравнений эллиптического типа – предназначена функция relax(a, b, c, d, e, f, u, rjac), реализующая метод релаксации. Фактически, эту функцию можно использовать для решения эллиптического уравнения общего вида
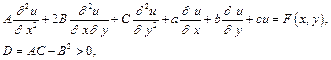
которое может быть сведено к уравнению в конечных разностях
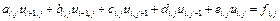
В частности, для уравнения Пуассона коэффициенты 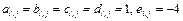 .
.
Идея метода релаксации заключается в следующем. Если нет источников (уравнение Лапласа), то значение функции в данном узле на текущем шаге 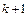 определяется как среднее значение функции в ближайших узлах на предыдущем шаге k
определяется как среднее значение функции в ближайших узлах на предыдущем шаге k
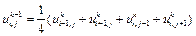
При наличии источников разностная схема имеет вид 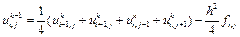
Метод релаксации сходится достаточно медленно, так как фактически он использует разностную схему с максимально возможным для двумерного случая шагом 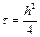 .
.
В методе релаксации необходимо задать начальное приближение, то есть значения функции во всех узлах области, а так же граничные условия.
Функция relax возвращает квадратную матрицу, в которой:
1) расположение элемента в матрице соответствует его положению внутри квадратной области,
2) это значение приближает решение в этой точке.
Эта функция использует метод релаксации для приближения к решению.
Вы должны использовать функцию relax, если Вы знаете значения искомой функции u(x, y) на всех четырех сторонах квадратной области.
Аргументы:
a, b, c, d, e – квадратные матрицы одного и того же размера, содержащие коэффициенты дифференциального уравнения.
f – квадратная матрица, содержащая значения правой части уравнения в каждой точке внутри квадрата
u – квадратная матрица, содержащая граничные значения функции на краях области, а также начальное приближение решения во внутренних точках области.
rjac – Параметр, управляющий сходимостью процесса релаксации. Он может быть в диапазоне от 0 до 1, но оптимальное значение зависит от деталей задачи.
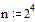
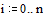
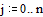
Задаем правую часть уравнения Пуассона – два точечных источника
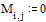
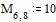
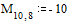
Задаем значения параметров функции relax
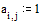
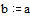

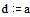
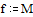
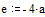
Задаем граничные условия и начальное приближение – нули во всех внутренних точках области
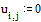
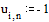
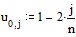
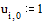
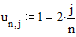
Находим решение 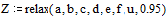
и представляем его графически в виде поверхности и линий уровней.
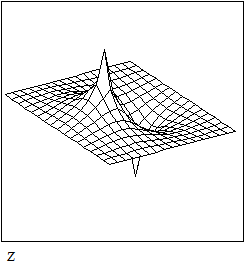

Если граничные условия равны нулю на всех четырех сторонах квадрата, можно использовать функцию multigrid.
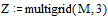
Алгоритм метода достаточно громоздкий, поэтому рассматривать его мы не будем.
 2015-02-15
2015-02-15 965
965








